P3205 [HNOI2010]合唱队

题面

输入格式

第一行一个整数 n
第二行 n 个整数，表示小 A 心中的理想队形。

输出格式

输出一行一个整数，表示答案 \(\bmod 19650827\) 的值。

输入输出样例

输入 #1

4
1701 1702 1703 1704

输出 #1

8

说明/提示

对于 30%的数据，n≤100n
对于 100% 的数据，n≤1000 ,1000≤hi≤2000.

一道很妙的区间dp题。

我们可以套用区间dp的套路设f[i][j]表示从i到j的方案数。

可这样你会发现无法区分一个人是从那边进来的。

所以我们在添上一维 f[i][j][0/1] 表示从i到j最后一个人是从左边或右边进来的方案数。

这时候，我们就开始大力讨论转移。

首先，当从左边进来的时候，红色为上个人所在的位置

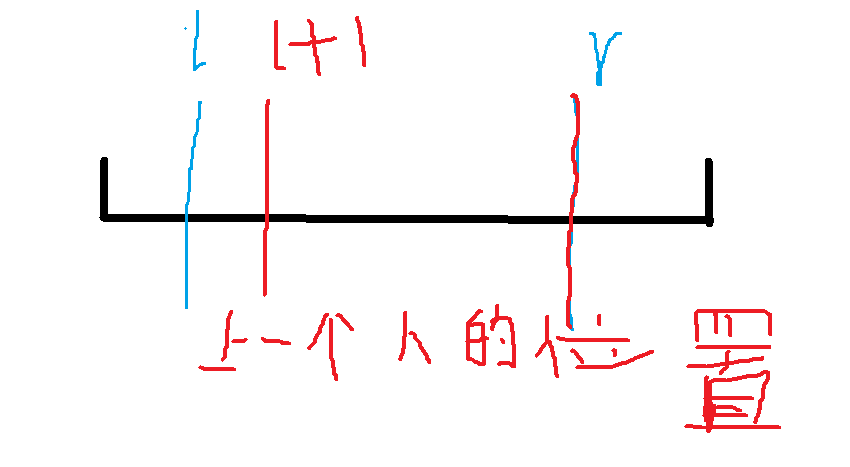
1. 他前一个人在l+1的时候，此时可以加上f[l+1][r][0]的方案数

2. 他前一个人在r的时候，就可以加上f[l+1][r][1]的方案数

第二种情况就是这个人从右边进来的时候，（其实和从左边进来的没什么区别，雾）。

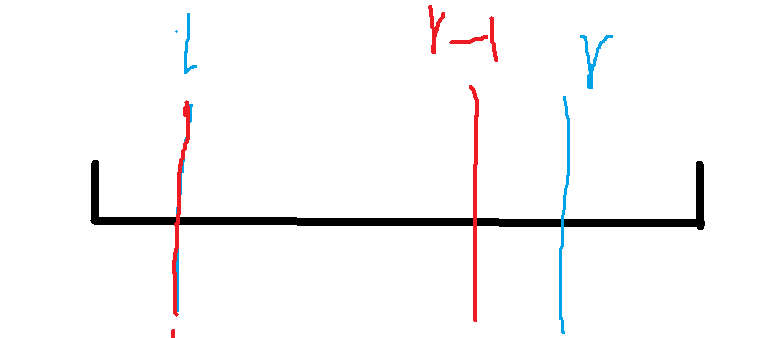
1. 他前一个人在l的时候，加上f[l][r-1][0]就可以了

2. 前一个人在r-1的时候，加上f[l][r-1][1]的方案数。

转移时判断一下是否满足 “如果他比前面那个人高（h 较大），那么将他插入当前队形的最右边。如果他比前面那个人矮（h 较小）

那么将他插入当前队形的最左边。”这个条件就行了。

转移方程

    if(h[l] < h[l+1]) f[l][r][0] = (f[l][r][0] + f[l+1][r][0]) % p;
    if(h[r] > h[r-1]) f[l][r][1] = (f[l][r][1] + f[l][r-1][1]) % p;
    if(h[l] < h[r]) f[l][r][0] = (f[l][r][0] + f[l+1][r][1]) % p;
    if(h[r] > h[l]) f[l][r][1] = (f[l][r][1] + f[l][r-1][0]) % p;	

注意初始化的时候不可以写成f[i][i][0] = f[i][i][1] = 1（就算你除以2过了样例也会WA）

因为，他一个人的时候，从左边进和从右边进都是一样的，这样我们会重复计算。

最后统计答案的时候考虑最后一个时从左边进还是右边进，f[1][n][1]+f[1][n][0]就完事啦。

所以，之后一个人的时候，我们就默认他是从左边进的进行啦。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int p = 19650827;
int n,f[1010][1010][2],h[1010];
inline int read()
{
	int s = 0, w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10+ch -'0'; ch = getchar();}
	return s * w; 
}
int main()
{
	n = read();
	for(int i = 1; i <= n; i++) h[i] = read();
	for(int i = 1; i <= n; i++) f[i][i][0] = 1;//初始化
	for(int len = 2; len <= n; len++)//枚举长度
	{
		for(int l = 1; l + len-1 <= n; l++)//枚举左端点
		{
			int r = l+len-1;
			if(h[l] < h[l+1]) f[l][r][0] = (f[l][r][0] + f[l+1][r][0]) % p;//大力转移
			if(h[r] > h[r-1]) f[l][r][1] = (f[l][r][1] + f[l][r-1][1]) % p;
			if(h[l] < h[r]) f[l][r][0] = (f[l][r][0] + f[l+1][r][1]) % p;
			if(h[r] > h[l]) f[l][r][1] = (f[l][r][1] + f[l][r-1][0]) % p;		
		}
	}
	int ans = (f[1][n][0] + f[1][n][1]) % p;//统计答案
	printf("%d\n",ans);
	return 0;
}

ENDING