P2704 [NOI2001]炮兵阵地
司令部的将军们打算在 (N imes M)的网格地图上部署他们的炮兵部队。一个 (N imes M)的地图由 (N) 行 (M) 列组成,地图的每一格可能是山地(用“ (H) ” 表示),也可能是平原(用“ (P) ”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
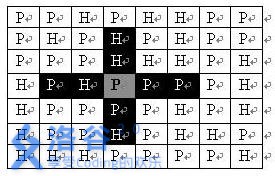
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示 (N) 和 (M);
接下来的 (N) 行,每一行含有连续的 (M) 个字符(‘ (P) ’或者‘(H) ’),中间没有空格。按顺序表示地图中每一行的数据。(N≤100);(M≤10)。
输出格式
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
输入输出样例
输入 #1
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出 #1
6
比较有意思的状压 (dp).
考虑到每一行的状态与他的前两行状态有关,我们可以枚举这三行的状态来转移。
设 (f[i][j][k]) 表示 前 (i) 行,且第 (i) 行的放置状态为 (j) ,且第 (i-1) 行的状态为 (k) 的最大能放置的方案数。
转移时,枚举这三行的状态,判断一下这三行状态是否合法就可以。就有转移:
(f[i][j][k] += f[i-1][k][s] + cnt[j]) ((cnt[j]) 为 (j) 能放的炮的数量)。
可你这样复杂度会很高。但你会发现每行的合法状态会很少。
所以,我们可以预处理出合法的状态,以及这个状态能放炮的数量。
转移时直接利用合法状态转移就可以啦。
Code:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = (1<<10)+1;
int n,m,cnt,num,ans,t[110];
char s[110];
int f[110][N][N],zt[N],pao[N];
int main()
{
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++)
{
scanf("%s",s+1);
int len = strlen(s+1);
for(int j = 1; j <= len; j++)
{
if(s[j] == 'H') t[i] += (1<<(j-1));//每一行能不能放的状态
}
// cout<<t[i]<<endl;
}
for(int i = 0; i <= (1<<m)-1; i++)//预处理每一行的合法状态
{
if((i & (i>>1)) == 0 && (i & (i>>2)) == 0)//左移和右移的结果一样,只需要判断一种是否满足就可以
{
zt[++num] = i;
// cout<<num<<endl;
}
}
for(int i = 1; i <= num; i++)//求出每个状态能放炮的数量
{
int x = zt[i];
cnt = 0;
while(x)
{
if(x & 1) cnt++;
x >>= 1;
}
// cout<<zt[i]<<" "<<cnt<<endl;
pao[i] = cnt;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= num; j++)//大力转移
{
if(zt[j] & t[i]) continue;//如果这个状态放到了这一行不能放的位置即山地就接着枚举
for(int k = 1; k <= num; k++)
{
if((zt[k] & t[i-1]) || (zt[j] & zt[k])) continue;//k状态不能放到 i-1 这一行的山地位置,以及同一列上不能放相邻的两个
for(int u = 1; u <= num; u++)//枚举 i-2 行的状态
{
if((zt[u] & t[i-2]) || (zt[k] & zt[u]) || (zt[j] & zt[u])) continue;//不能和 i行以及 i-1 行的状态发生矛盾
f[i][j][k] = max(f[i][j][k],f[i-1][k][u]+pao[j]);//转移
}
ans = max(ans,f[i][j][k]);//更新答案
}
}
}
printf("%d
",ans);
return 0;
}