本文中的图片摘自 这篇文章。
什么是二者取一式问题呢?
简单来说就是你现在有两个集合 (A) 和 (B), 一件物品放 (A) 集合的收益为 (a_i), 放 (B) 集合的收益为 (b_i) 。
另外有, (x) 和 (y) 两种物品同时属于 (A) 集合的额外收益为 (a'_i) ,同时属于 (B) 集合的额外收益为 (b'_i) 。
怎么求呢?
这个问题可以转化为网络流的最小割模型。
首先,如果不看额外收益的话,我们可以建一个这样的图出来。
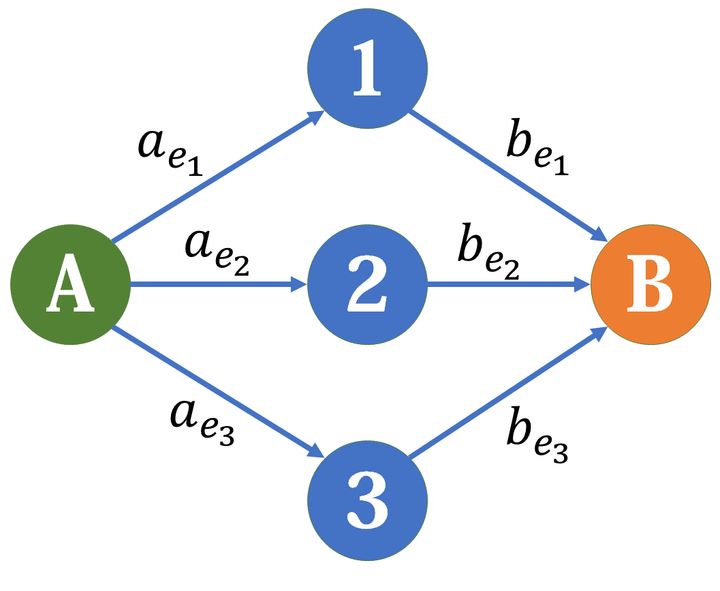
你会发现我们求出来的最小割是每个物品的 (a_i) 和 (b_i) 的最小值之和,设边权总和为 (sum), 那么最后的答案就是 (sum - 最小 割) 。
接下来我们继续解决额外收益的问题。
假设 (1) 和 (2) 同时属于 (A) 集合的额外收益为 $a'_i $ ,我们开一个虚点 $x $ 表示这个组合,从源点向 (x) 连一条容量为 (a'_i) 的边。
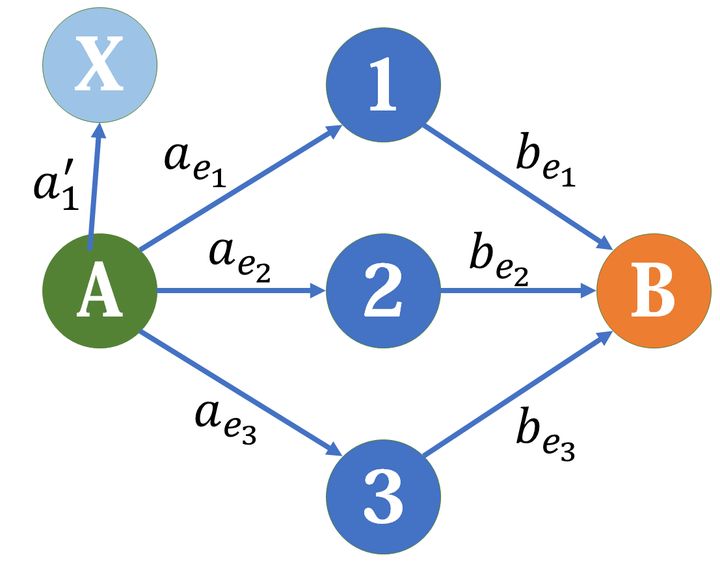
我们现在想让 (1) 和 (2) 同时属于 (A) 集合的时候才会有额外收益,反过来想就是如果 (1) 属于 (B) 集合的话,就需要让 (Ax) 这一条边割掉,所以由 (x) 向 (1,2) 分别连一条边,这样可以保证当 (1) 属于 (B) 集合的时候, (A-x-1) 这条边会被割掉。那么这条边的容量为多少呢? 不难想到如果我们这条边的边权比 (a'_i) 小,那么 (x-1) 这条边就会被割掉,对答案产生影响。 所以我们要让这条边的边权尽可能的大,边权设为正无穷即可。 (2) 号点同理。
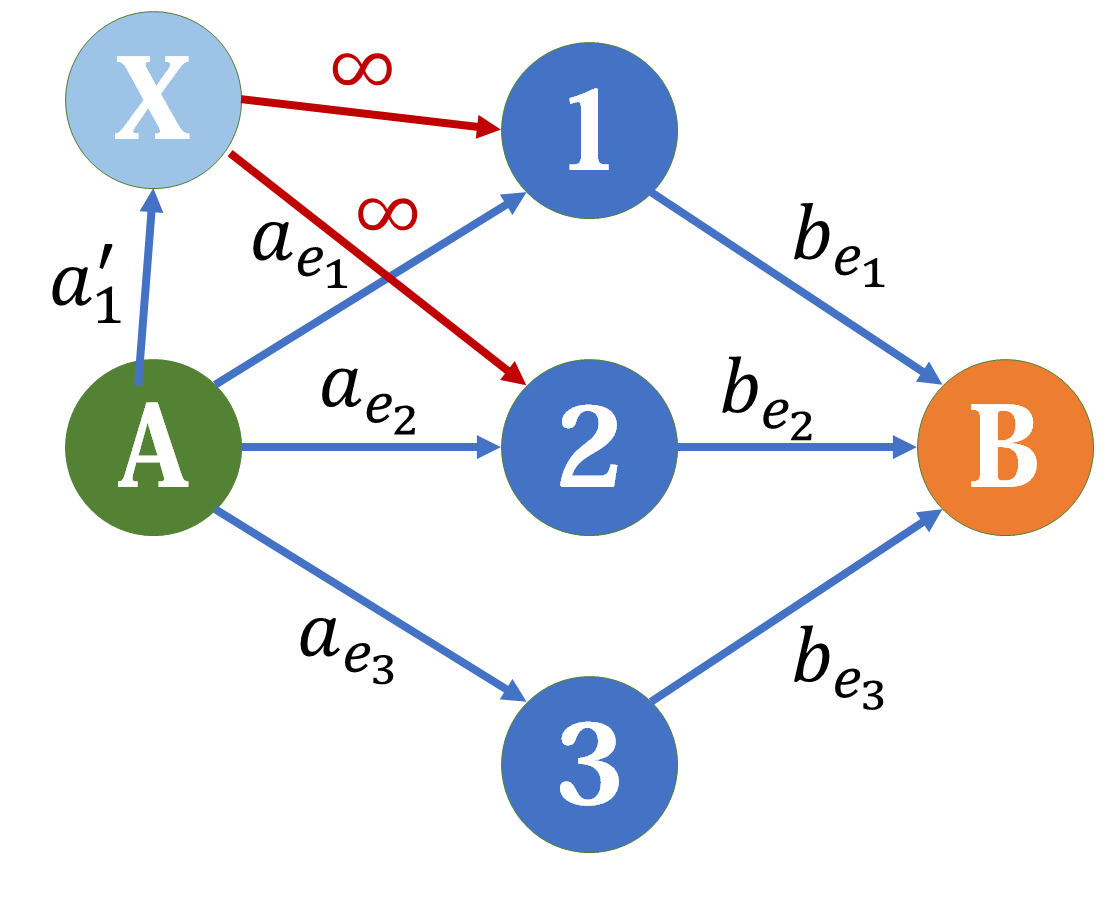
对于 (B) 点同理,最后得到的图长成这个样子:
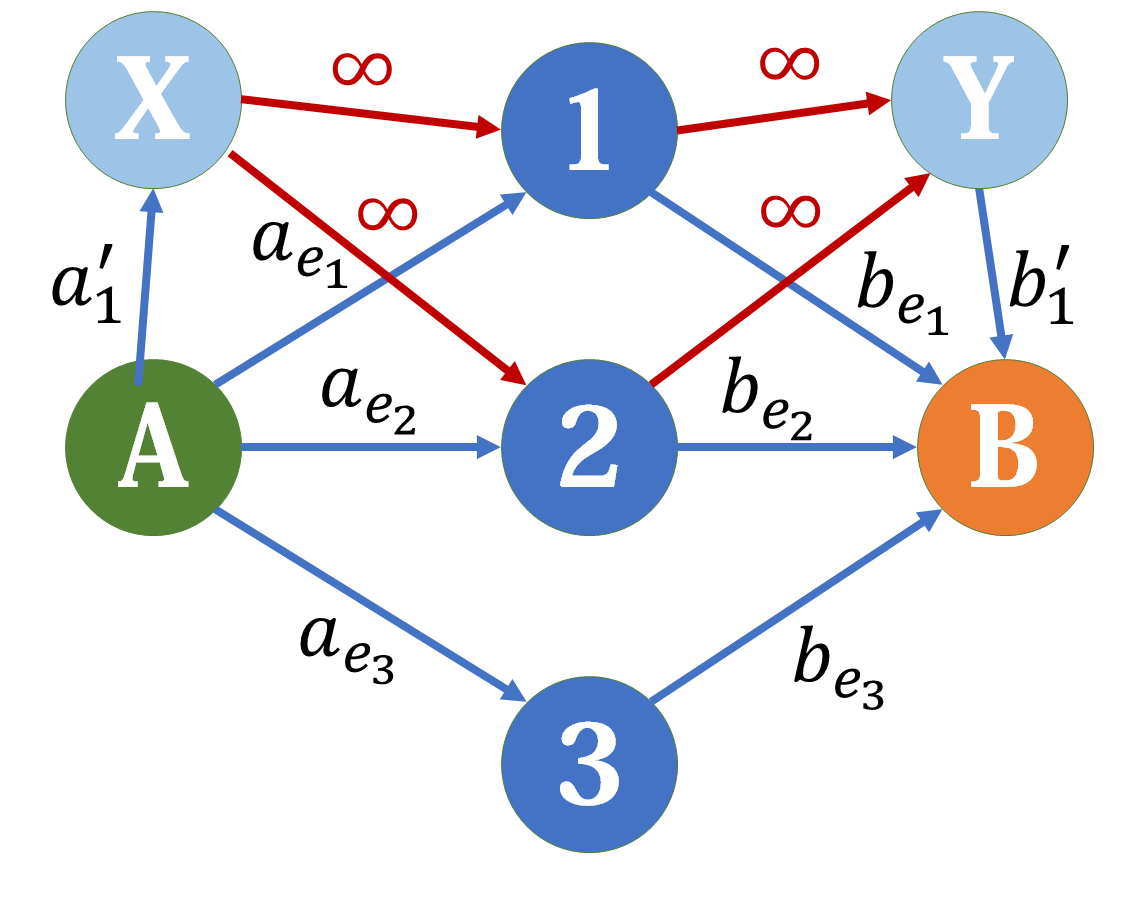
总结一下建图思路:源点和汇点分别表示两个集合,对于每个点,由源点向这个点连一条容量为 (a_i) 的边,再由这个点向汇点连一条容量为 (b_i) 的边。对于每种组合,新开一个虚拟节点表示这个组合,由源点向这个点连一条容量为 (a'_i) 的边(这个点向汇点连一条容量为 $b'_i $ 的边) ,再由这个虚拟节点向这个组合中的点连一条容量为 (inf) 的边,最后的答案就是总的边权和减去最小割。
例题:
把文理科看做两个集合,按上述连边方案连边即可。注意点数要开大点。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 50010;
const int inf = 1e7+10;
int n,m,s,t,w,sum,cnt,ans,tot = 1;
int head[N],dep[N],id[510][510];
struct node
{
int to,net,w;
}e[1000010];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
void add(int x,int y,int w)
{
// cout<<x<<" "<<y<<" "<<w<<endl;
e[++tot].to = y;
e[tot].w = w;
e[tot].net = head[x];
head[x] = tot;
}
bool bfs()
{
queue<int> q;
for(int i = 0; i <= t; i++) dep[i] = 0;
q.push(s); dep[s] = 1;
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(e[i].w && !dep[to])
{
dep[to] = dep[x] + 1;
q.push(to);
if(to == t) return 1;
}
}
}
return 0;
}
int dinic(int x,int flow)
{
if(x == t || !flow) return flow;
int rest = flow, val;
for(int i = head[x]; i && rest; i = e[i].net)
{
int to = e[i].to;
if(!e[i].w || dep[to] != dep[x] + 1) continue;
val = dinic(to,min(rest,e[i].w));
if(val == 0) dep[to] = 0;
e[i].w -= val; e[i ^ 1].w += val; rest -= val;
}
return flow - rest;
}
int main()
{
n = read(); m = read(); s = 0, t = 5*n*m;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
id[i][j] = ++cnt;
w = read(); sum += w;
add(s,id[i][j],w); add(id[i][j],s,0);
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
w = read(); sum += w;
add(id[i][j],t,w); add(t,id[i][j],0);
}
}
for(int i = 1; i <= n-1; i++)
{
for(int j = 1; j <= m; j++)
{
w = read(); cnt++; sum += w;
add(s,cnt,w); add(cnt,s,0);
add(cnt,id[i][j],inf); add(id[i][j],cnt,0);
add(cnt,id[i+1][j],inf); add(id[i+1][j],cnt,0);
}
}
for(int i = 1; i <= n-1; i++)
{
for(int j = 1; j <= m; j++)
{
w = read(); cnt++; sum += w;
add(cnt,t,w); add(t,cnt,0);
add(id[i][j],cnt,inf); add(cnt,id[i][j],0);
add(id[i+1][j],cnt,inf); add(cnt,id[i+1][j],0);
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m-1; j++)
{
w = read(); cnt++; sum += w;
add(s,cnt,w); add(cnt,s,0);
add(cnt,id[i][j],inf); add(id[i][j],cnt,0);
add(cnt,id[i][j+1],inf); add(id[i][j+1],cnt,0);
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m-1; j++)
{
w = read(); cnt++; sum += w;
add(cnt,t,w); add(t,cnt,0);
add(id[i][j],cnt,inf); add(cnt,id[i][j],0);
add(id[i][j+1],cnt,inf); add(cnt,id[i][j+1],0);
}
}
int flow = 0;
while(bfs())
{
while(flow = dinic(s,inf)) ans += flow;
}
printf("%d
",sum-ans);
return 0;
}