wdnmd,真就全都不会做呗。
(T1) 打了个自认为很对的算法,但和暴力一拍全是问题。
(T2) 题目长得太恶心了,没仔细看。
(T3) 暴力分给的挺多的,但输入和预处理太恶心了,就没想写。
T1 次短路径 pal
题意描述
给出一个 (n) 个点、(m) 条边的无向图,求 (i) 号点((ileq n))在不经过到 (1) 号点的最短路径上的第一条边的情况下,到 (1) 号点的路径长度最小值。
数据保证 (i) 号点((ileq n))到 (1) 号点的最短路径上的第一条边是唯一确定的。
数据范围: (nleq 10^5,mleq 2 imes 10^5,wleq 1000)
solution
最短路径树加线段树合并。bzoj上一道类似的题。
我们先构建出整个图的最小路径生成树。具体怎么构造呢?
我们先用 (DIJ) 求出 (1) 到每个点的距离 (d_i) ,对于无向图中的一条边 ((u,v,w)) 如果 (d_u = d_v + w) 或者 (d_v = d_u+w)
那么这条边就是最小路径树上的边,否则为非树边。
又因为题目中保证了 (1) 号点到第 (i) 号点的最短路径是确定的。
所以可知最小路径树是一棵以 (1) 为根的树。
(u) 号点到 (1) 号点的最短路径上的第一条边就是 (u) 号点和他最短路径树上父亲的那一条边。
那么 一条从 (u) 出发的合法路径就是,从 (u) 走到子树中的一个节点 (v), 再从一条非树边 ((v,w)) 走到 (u) 子树外的一个点 (w) ,在从 (w) 这个点走回根节点。

设 (sum[i]) 表示最短路径树上从根节点到 (i) 号点的边权之和。
那么对于图中的合法路径的长度就可以表示为 (sum[v]+sum[w]+dis(v,w) - sum[u])
我们把 (sum[u]) 提出来,发现其他东西就和 (u) 无关了。
对每个点都建一棵以 (sum[v]+sum[w]+dis(v,w)) 为下标的权值线段树。
对于每一条非树边,当遍历到边的任意一个端点的时候把 (sum[v]+sum[w]+dis(v,w)) 加进去,在遍历到两个端点的 (lca) 的时候把 (sum[v]+sum[w]+dis(v,w)) 删掉。
需要支持合并,查询最小值,删除特定的值。
权值线段树套线段树合并,或左偏树即可。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 2e5+10;
const int inf = 2e8+10;
int n,m,u,v,w,cnt,tot,type;
int head[N],Head[N],dis[N],siz[N],son[N],fa[N],top[N],dep[N],sum[N],rt[N],ans[N];
bool vis[N],tag[N<<1];
vector<int> p1[N],p2[N];
struct node
{
int from,to,net,w;
}e[N<<1],E[N<<1];
struct Tree
{
int lc,rc,siz,id;
}tr[30000010];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
void add(int x,int y,int w)
{
e[++tot].from = x;
e[tot].to = y;
e[tot].w = w;
e[tot].net = head[x];
head[x] = tot;
}
void Add(int x,int y,int w)
{
E[++cnt].to = y;
E[cnt].w = w;
E[cnt].net = Head[x];
Head[x] = cnt;
}
void up(int o)
{
if(tr[tr[o].lc].id) tr[o].id = tr[tr[o].lc].id;
else tr[o].id = tr[tr[o].rc].id;
}
void insert(int &o,int l,int r,int x,int val)
{
if(!o) o = ++type;
if(l == r)
{
tr[o].siz += val;
if(tr[o].siz >= 1) tr[o].id = l;
else tr[o].id = 0;
return;
}
int mid = (l+r)>>1;
if(x <= mid) insert(tr[o].lc,l,mid,x,val);
if(x > mid) insert(tr[o].rc,mid+1,r,x,val);
up(o);
}
void merage(int &x,int y,int l,int r)
{
if(!x){x = y; return;}
if(!y) return;
if(l == r)
{
tr[x].siz += tr[y].siz;
if(tr[x].siz >= 1) tr[x].id = l;
else tr[x].id = 0;
return;
}
int mid = (l+r)>>1;
merage(tr[x].lc,tr[y].lc,l,mid);
merage(tr[x].rc,tr[y].rc,mid+1,r);
up(x);
}
void get_tree(int x,int w)
{
dep[x] = dep[fa[x]] + 1; siz[x] = 1; sum[x] = sum[fa[x]] + w;
for(int i = Head[x]; i; i = E[i].net)
{
int to = E[i].to;
if(to == fa[x]) continue;
fa[to] = x;
get_tree(to,E[i].w);
siz[x] += siz[to];
if(siz[to] > siz[son[x]]) son[x] = to;
}
}
void dfs1(int x,int topp)
{
top[x] = topp;
if(son[x]) dfs1(son[x],topp);
for(int i = Head[x]; i; i = E[i].net)
{
int to = E[i].to;
if(to == fa[x] || to == son[x]) continue;
dfs1(to,to);
}
}
int lca(int x,int y)
{
while(top[x] != top[y])
{
if(dep[top[x]] < dep[top[y]]) swap(x,y);
x = fa[top[x]];
}
return dep[x] <= dep[y] ? x : y;
}
void DIJ()
{
priority_queue<pair<int,int> > q;
for(int i = 1; i <= n; i++) dis[i] = 5e8+10;
dis[1] = 0; q.push(make_pair(0,1));
while(!q.empty())
{
int x = q.top().second; q.pop();
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(dis[to] > dis[x] + e[i].w)
{
dis[to] = dis[x] + e[i].w;
q.push(make_pair(-dis[to],to));
}
}
}
}
void dfs2(int x,int fa)
{
for(int i = 0; i < p1[x].size(); i++) insert(rt[x],1,inf,p1[x][i],1);
for(int i = 0; i < p2[x].size(); i++) insert(rt[x],1,inf,p2[x][i],-2);
for(int i = Head[x]; i; i = E[i].net)
{
int to = E[i].to;
if(to == fa) continue;
dfs2(to,x);
merage(rt[x],rt[to],1,inf);
}
if(tr[rt[x]].id == 0) ans[x] = -1;
else ans[x] = tr[rt[x]].id-dis[x];
}
int main()
{
// freopen("pal.in","r",stdin);
// freopen("pal.out","w",stdout);
n = read(); m = read();
for(int i = 1; i <= m; i++)
{
u = read(); v = read(); w = read();
add(u,v,w); add(v,u,w);
}
DIJ();
for(int i = 1; i <= tot; i++)//建最小路径生成树
{
int x = e[i].from, y = e[i].to;
if(dis[x] == dis[y] + e[i].w || dis[y] == dis[x] + e[i].w)
{
Add(x,y,e[i].w);
tag[i] = 1;
}
}
get_tree(1,0); dfs1(1,1);
for(int i = 1; i <= tot; i++)
{
int x = e[i].from, y = e[i].to;
if(tag[i] == 0)
{
p1[x].push_back(sum[x]+sum[y]+e[i].w);
p1[y].push_back(sum[x]+sum[y]+e[i].w);
p2[lca(x,y)].push_back(sum[x]+sum[y]+e[i].w);
}
}
dfs2(1,0);
for(int i = 2; i <= n; i++) printf("%d
",ans[i]);
fclose(stdin); fclose(stdout);
return 0;
}
T2 带权的图 graph
题意描述
给定一张连通无向图 (G = (V,E)) 与一个素数 (P),其中 (V) 是点集 (E) 是边集。
图中的每条边有三种权值 (A,B,C),但同一条边的两个方向上的权值不一定相等。更具体地,它们满足以下条件:
-
对于任意无向边 ((u,v)in E) 有:
(A(u,v) equiv -A(v,u)pmod P\B(u,v) equiv B(v,u) pmod P\C(u,v)equiv -C(v,u) pmod p)
-
对于任意结点 (vin V) 有:
(displaystylesum_{(v,w)in E} C(v,w) equiv 0 pmod P)
-
对于图中的任意一个环 ((v_0,v_1,.....v_{n-1},v_n)),其中 (v_0=v_n) 且 (v_i,v_{i+1}in E) ,有:
(displaystylesum_{i=0}^{n-1}Bleft(v_{i},v_{i+1} ight)cdot Cleft(v_{i},v_{i+1} ight) equiv sum_{i=0}^{n-1} Aleft(v_{i},v_{i+1} ight)pmod P)
现在给定图中每条边的权值 (A,B) ,请你求出 (C) 的取值。数据保证有唯一解。
数据范围:点数 (nleq 100), 边数 (mleq 2000) 。
solution
高斯消元加构造。
咕咕咕 cy。
T3 木棍问题 trouble
小 A 有一些木球,他把这些木球放置于一个 (n) 行 (m) 列的网格中,其中每一格最多放置了一个木球。
定义每个木球和它上下左右四个木球(如果存在)是相邻的。
小 A 想在网格中插入 (k) 个木棍,每个木棍只能插在相邻的两个木球之间,且任意两个相邻的木球之间最多插入一个木棍。
小 A 为此特意请来一位木匠。但由于木球材质不好,木匠需要高超的技术才能完成。
具体来说,对于任意两个木棍,若它们的某个端点是相同的木球,那么这个木球容易碎裂,此时木匠会向小A收取费用:
- 若两个木棍呈现 L 形,木匠会收取费用 (A);
- 若两个木棍呈现 I 形,由于两个木棍互相挤压,木球更易碎裂,木匠会收取费用 (B(Bgeq A)) 。
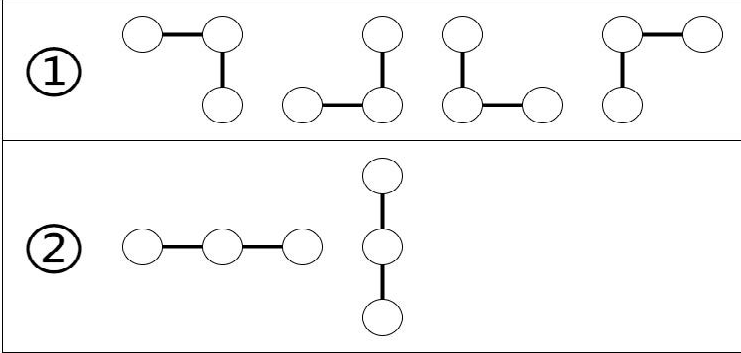
小 A 金钱十分有限,他想要知道:如果可以任意安排 (k) 个木棍的位置,那么为了插入所有木棍,至少要给木匠多少费用。
对于任意的 (1leq kleq q) ,输出答案。其中 (q) 为可插入的木棍总数
数据范围: (nleq 40,mleq 40), (q=) 可插入的木棍总数。
solution
构造费用流
咕咕咕。