省选模拟测试25

考的广西 (2019) 年省选的 (DAY1)。

(T1) 很裸的单调栈，但自己的做法被卡常了，比正解要多个 (4) 倍常数，在机房的老年机上要跑 (5s+) 。

(T2) 自己之前没做过这种麻将题，考试的时候一点思路都没有。

(T3) 不说了，毒瘤计算几何题。

T1 与或和

题意描述

Freda 学习了位运算和矩阵以后，决定对这种简洁而优美的运算，以及蕴含深邃空间的结构进行更加深入的研究。

对于一个由非负整数构成的矩阵，她定义矩阵的 (AND) 值为矩阵中所有数二进制 ( ext{AND(&)}) 的运算结果；定义矩阵的 (OR) 值为矩阵中所有数二进制 (OR(|)) 的运算结果。

给定一个 (N×N) 的矩阵，她希望求出：

1. 该矩阵的所有子矩阵的 (AND) 值之和（所有子矩阵 (AND) 值相加的结果）。
2. 该矩阵的所有子矩阵的 (OR) 值之和（所有子矩阵 (OR) 值相加的结果）。

接下来的剧情你应该已经猜到——Freda 并不想花费时间解决如此简单的问题，所以这个问题就交给你了。由于答案可能非常的大，你只需要输出答案对 (1,000,000,007 (1e9 + 7)) 取模后的结果。

数据范围：(1leq nleq 1000) 。

solution

单调栈。

不难想到按位来进行处理。

考虑有多个子矩阵的值 ( ext{AND}) (( ext{OR})) 值这一位为 (1) 。

不难发现我们其实要统计全为 (0/1) 的子矩阵的个数。

直接用单调栈来维护即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 2010;
const int p = 1e9+7;
int n,ans1,ans2,num1,num2;
int a[N][N],b[N][N],h[N][N],sta[N],ls[N],rs[N];
inline int read()
{
    int s = 0,w = 1; char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
    while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
    return s * w;
}
void work()
{
    for(int j = 1; j <= n; j++)
    {
        int mn = n+1;
        for(int i = n; i >= 1; i--)
        {
            if(b[i][j] == 0) mn = min(mn,i), h[i][j] = 0;
            else h[i][j] = mn-i;
        }
    }
    for(int i = 1; i <= n; i++)
    {
        int top = 0; h[i][0] = 0; sta[++top] = 0;
        for(int j = 1; j <= n; j++)
        {
            while(top && h[i][sta[top]] > h[i][j]) top--;
            ls[j] = sta[top]; sta[++top] = j; 
        }
        top = 0; h[i][n+1] = 0; sta[++top] = n+1;
        for(int j = n; j >= 1; j--)
        {
            while(top && h[i][sta[top]] >= h[i][j]) top--;
            rs[j] = sta[top]; sta[++top] = j;
        }
        for(int j = 1; j <= n; j++) num1 = 1LL * (num1 + 1LL * h[i][j] * (j-ls[j]) % p * (rs[j]-j) % p) % p;
    }
    for(int j = 1; j <= n; j++)
    {
        int mn = n+1;
        for(int i = n; i >= 1; i--)
        {
            if(b[i][j] == 1) mn = min(mn,i), h[i][j] = 0;
            else h[i][j] = mn-i;
        }
    }
    for(int i = 1; i <= n; i++)
    {
        int top = 0; h[i][0] = 0; sta[++top] = 0;
        for(int j = 1; j <= n; j++)
        {
            while(top && h[i][sta[top]] > h[i][j]) top--;
            ls[j] = sta[top]; sta[++top] = j; 
        }
        top = 0; h[i][n+1] = 0; sta[++top] = n+1;
        for(int j = n; j >= 1; j--)
        {
            while(top && h[i][sta[top]] >= h[i][j]) top--;
            rs[j] = sta[top]; sta[++top] = j;
        }
        for(int j = 1; j <= n; j++) num2 = 1LL * (num2 + 1LL * h[i][j] * (j-ls[j]) % p * (rs[j]-j) % p) % p;
    }
}
int main()
{
//	freopen("andorsum.in","r",stdin);
//	freopen("andorsum.out","w",stdout);
    n = read(); int sum = n*(n+1)/2; sum = 1LL * sum * sum % p;
    for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) a[i][j] = read();
    for(int i = 0; i <= 30; i++)
    {
        num1 = num2 = 0;
        for(int j = 1; j <= n; j++)
        {
            for(int k = 1; k <= n; k++)
            {
                b[j][k] = (a[j][k]>>i)&1; 
            }
        }
        work();
        int tmp = 1LL<<i;
        ans1 = 1LL * (ans1 + 1LL * num1 * tmp % p) % p;
        ans2 = 1LL * (ans2 + 1LL * (sum - num2 % p + p) % p * tmp % p) % p;
    }
    printf("%d %d
",ans1,ans2);
    fclose(stdin); fclose(stdout);
    return 0;
}

T2 宝牌一大堆

麻将是一种传统的博弈游戏，由 (4) 名玩家参与，轮流摸牌、打牌。在竞技比赛中主要有国标麻将（中国）和立直麻将（日本）两大规则。本题采用一种特别的规则——「宝牌一大堆」规则。

牌型

一副麻将由 (136) 张牌组成，其中包含 (34) 种不同的牌，每种各有 (4) 张。这 (34) 种牌分别是：
一万到九万、一索到九索、一筒到九筒、东、南、西、北、中、白、发。

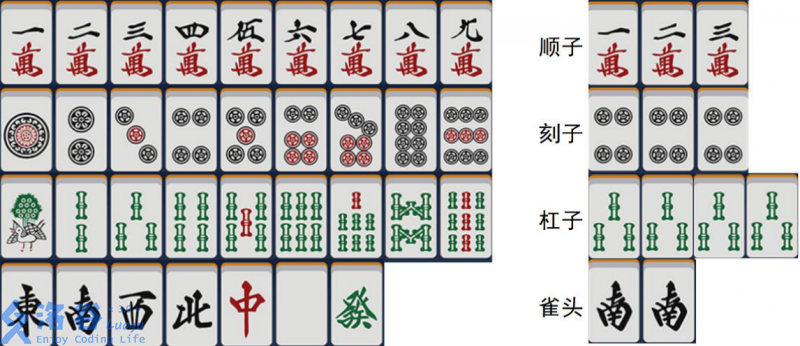
它们可以组合成不同的牌型：

• 顺子：(3) 张数字连续的万，或 (3) 张数字连续的索，或 (3) 张数字连续的筒。
• 刻子：(3) 张完全一样的牌。
• 杠子：(4) 张完全一样的牌。
• 雀头：(2) 张完全一样的牌。

其中顺子和刻子统称为面子。

和牌

手牌（一名玩家持有的牌）宣告胜利的状况称为「和牌」。

• 当玩家持有 (14) 张牌，并且满足以下三个条件之一时，判定为「和牌」：
  1. 存在一种方案，使得这 (14) 张牌可以分成 (4) 组面子、(1) 组雀头，简记为 (「3 imes 4 + 2」)$。
  2. 存在一种方案，使得这 (14) 张牌可以分成 (7) 组不同的雀头，称为「七对子」。
  3. 这 (14) 张牌仅由一万、九万、一索、九索、一筒、九筒、东、南、西、北、中、白、发这 (13) 种牌组成，并且这 (13) 种牌每种至少有 1 张，称为「国士无双」。
• 当玩家持有 (15) 张牌，并且存在一种方案，使得这 (15) 张牌可以分成 (1) 组杠子、(3) 组面子、(1) 组雀头，判定为和牌。
• 当玩家持有 (16) 张牌，并且存在一种方案，使得这 (16) 张牌可以分成 (2) 组杠子、(2) 组面子、(1) 组雀头，判定为和牌。
• 当玩家持有 (17) 张牌，并且存在一种方案，使得这 (17) 张牌可以分成 (3) 组杠子、(1) 组面子、(1) 组雀头，判定为和牌。
• 当玩家持有 (18) 张牌，并且存在一种方案，使得这 (18) 张牌可以分成 (4) 组杠子、(1) 组雀头，判定为和牌。

宝牌

每局游戏还会指定若干张「宝牌」，和牌时，手牌中的每张宝牌会使收益翻一番（会在接下来详细介绍）。

达成分数

由于可以「和牌」的手牌很多，可以给每种判定为「和牌」的手牌定义一个「达成分数」，这个分数等于从所有尚未打出的牌中选出若干张，能够组成该手牌的方法数，再乘上手牌中 (2) 的「宝牌数」次方。
该分数综合考虑了和牌几率与和牌收益，理论上以分数较高的手牌为目标较好。

例如下图手牌显然是可以「和牌」的，如果目前场上还剩 (3) 张一万、(4) 张九万，以及二到八万各 (2) 张没有打出，宝牌为九万，那么下图手牌的「达成分数」就是 (C_3^3 C_4^3 C_2^2 (C_2^1)^6 2^3 = 2048)，其中 (C) 表示组合数。

特别地，「七对子」和牌的手牌，达成分数额外乘 (7)。「国士无双」和牌的手牌，达成分数额外乘 (13)。

有一天，小 L，小 Y，小 I 和小 W 正在打麻将，路过的雪野和看到了所有已经打出的牌，但不知道任何一名玩家的手牌。也许你已经猜到了下面的剧情— —雪野和想知道在所有尚未打出的牌中，「达成分数」最高的可以「和牌」的手牌有多少分，但是她还要观看麻将比赛，所以这个问题就交给你了。

数据范围： (Tleq 2500,宝牌数leq 20) 。

solution

动态规划（传说中的麻将类dp）。

简化题意：给你一些已经使用过的牌，让你从没使用过的牌中选出一组能够胡牌的组合，问这个组合的最大达成分数为多少。

首先考虑一个问题就是杠子是没有刻子要优的。因为 ({4choose 1} < {4choose 3})， 也就是说当你选了杠子的时候，舍弃一张牌让其变成刻子是要更优的。

然后我们的胡牌方式就变成了三种：七对子，国土无双，(3 imes 4+2) 。

分三种情况讨论一下：

第一种情况：七对子胡牌

这种情况很好处理，只需要开个堆，维护每种牌组成雀头的最大价值。取堆中前 (7) 大的即可。

第二种情况：国土无双胡牌

枚举那一种牌出现了两次，算一下每种情况的答案，最后在取个 (min) 即可。

复杂度：(O(13^2)) 。

第三种情况：(3 imes 4+2)

这种情况就比较难处理了，考虑用 (dp) 来解决这个问题。

设 (f(i,j,k,u,v,w) (kin {0,1})) 表示前 (i) 种牌，组成 (j) 对面子，(k) 对雀头，其中第 (i,i+1,i+2) 分别选了 (u,v,w) 张的最大价值。

分 刻子/顺子/雀头/直接转移四种情况考虑。

• 直接转移：

  $ f(i+1,j,k,0,v,w) = f(i,j,k,u,v,w)$

• 雀头：

  $ f(i,j,k+1,u+2,v,w) = f(i,j,k,u,v,w) imes {{num[i]choose u+2}over {num[i]choose u}} imes (good[i])^2$

  中间拿两个组合数相除的意思为先把 (i) 在 (f(i,j,k,u,v,w)) 中的贡献 (num[i]choose u) 除去，在算上其在 (f(i,j,k,u+2,v,w)) 的贡献 (num[i]choose u+2) 。((good[i])^2) 则算的是新加入的两张 (i) 类型的牌的宝牌分数。

• 刻子：

  $ f(i,j+1,k,u+3,v,w) = f(i,j,k,u,v,w) imes {{num[i]choose u+3}over {num[i]choose u}} imes (good[i])^3$

  这个其实和上面雀头的转移是类似的。

• 顺子：
  $ f(i,j+1,k,u+1,v+1,w+1) = f(i,j,k,u,v,w) imes {{num[i]choose u+1}over {num[i]choose u}} imes {{num[i+1]choose v+1}over {num[i+1]choose v}} imes {{num[i+2]choose w+1}over {num[i+2]choose w}} imes good[i] imes good[i+1] imes good[i+2]$

  和上面的刻子的转移时类似的，就是考虑先把 (i,i+1,i+2) 在 (f(i,j,k,u,v,w)) 乘上的组合数除去，在乘上其在 (f(i,j+1,k,u+1,v+1,w+1)) 的组合数，同时在算上选 (i,i+1,i+2) 的宝牌分数即可。

然后这样我们就可以直接暴力 (dp) 了，复杂度：(O(T imes 34 imes 2 imes 4^4)) 。

这样只能得到 (60pts) 的分数。

考虑优化一下，其实当 (f(i,j,k,u,v,w) = 0) 的时候，我们是没必要用它来进行转移的.

用这个优化就可以省去不少无用状态,然后这道题就可以过了。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
#define int long long
int T,ans,c[50][50],num[50],good[50],f[36][5][2][5][5][5];
int a[50] = {0,1,9,10,18,19,27,28,29,30,31,32,33,34};
bool can[50] = {0,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0};
char s[5];
void YYCH()
{
	c[0][0] = 1;
	for(int i = 1; i <= 4; i++)
	{
		c[i][0] = c[i][i] = 1;
		for(int j = 1; j < i; j++)
		{
			c[i][j] = c[i-1][j] + c[i-1][j-1];
		}
	}
}
int bianhao(char s[3])
{
    if(s[1] >= '0' && s[1] <= '9')
    {
        if(s[2] == 'm') return s[1] - '0';
        if(s[2] == 'p') return 9 + s[1] - '0';
        if(s[2] == 's') return 18 + s[1] - '0';
    }   
    if(s[1] == 'E') return 28;
    if(s[1] == 'S') return 29;
    if(s[1] == 'W') return 30;
    if(s[1] == 'N') return 31;
    if(s[1] == 'Z') return 32; 
    if(s[1] == 'B') return 33;
    if(s[1] == 'F') return 34;
}
int C(int x,int y){return c[x][y];}
int Qiduizi()
{
    priority_queue<int> q;
    for(int i = 1; i <= 34; i++)
    {
        if(num[i] >= 2) q.push(C(num[i],2)*good[i]*good[i]);
    }
    if(q.size() < 7) return 0;
    int res = 1, cnt = 0;
    while(cnt < 7) cnt++, res *= q.top(), q.pop();
    return res*7;
}
int Guotuwushuang()
{
    for(int i = 1; i <= 13; i++) if(!num[a[i]]) return 0;
    int ans = 0;
    for(int i = 1; i <= 13; i++)
    {
        int res = 13 * C(num[a[i]],2) * good[a[i]] * good[a[i]];
        for(int j = 1; j <= 13; j++) if(j != i) res = res * C(num[a[j]],1) * good[a[j]];
        ans = max(ans,res);
    }
    return ans;
}
int dp()
{
    memset(f,0,sizeof(f));//前i张牌，j对面子，k对雀头，第i,i+1,i+2 的牌的数量的最大价值。
    f[1][0][0][0][0][0] = 1;
    for(int i = 1; i <= 34; i++)
    {
        for(int j = 0; j <= 4; j++)
        {
            for(int k = 0; k <= 1; k++)
            {
                for(int u = 0; u <= 4; u++)
                {
                    for(int v = 0; v <= 4; v++)
                    {
                        for(int w = 0; w <= 4; w++)
                        {
                        	if(!f[i][j][k][u][v][w]) continue;
                            if(k == 0 && u+2 <= num[i]) f[i][j][1][u+2][v][w] = max(f[i][j][1][u+2][v][w],f[i][j][k][u][v][w]/C(num[i],u)*C(num[i],u+2)*good[i]*good[i]);
                            if(j+1 <= 4 && u+3 <= num[i]) f[i][j+1][k][u+3][v][w] = max(f[i][j+1][k][u+3][v][w],f[i][j][k][u][v][w]/C(num[i],u)*C(num[i],u+3)*good[i]*good[i]*good[i]);
                            if(j+1 <= 4 && can[i] && u+1 <= num[i] && v+1 <= num[i+1] && w+1 <= num[i+2]) f[i][j+1][k][u+1][v+1][w+1] = max(f[i][j+1][k][u+1][v+1][w+1],f[i][j][k][u][v][w]/C(num[i],u)*C(num[i],u+1)/C(num[i+1],v)*C(num[i+1],v+1)/C(num[i+2],w)*C(num[i+2],w+1)*good[i]*good[i+1]*good[i+2]); 
                            if(i <= 34) f[i+1][j][k][v][w][0] = max(f[i+1][j][k][v][w][0],f[i][j][k][u][v][w]);
                        }
                    }
                }
            }
        }
    }
    int ans = 0;
    for(int i = 1; i <= 34; i++)
    {
    	for(int j = 0; j <= 4; j++)
    	{
        	for(int k = 0; k <= 4; k++)
        	{
            	for(int u = 0; u <= 4; u++)
            	{
                	ans = max(ans,f[i][4][0][j][k][u]);
                	ans = max(ans,f[i][4][1][j][k][u]);
            	}
        	}
    	}
    }
    return ans;
}
signed main()
{
    scanf("%d",&T); YYCH();
    while(T--)
    {
        ans = 0;
        for(int i = 1; i <= 34; i++) num[i] = 4, good[i] = 1;
        while(scanf("%s",s+1) != EOF && s[1] != '0') num[bianhao(s)]--;
        while(scanf("%s",s+1) != EOF && s[1] != '0') good[bianhao(s)] = 2;
        ans = max(ans,Guotuwushuang());
        ans = max(ans,Qiduizi());
        ans = max(ans,dp());
        printf("%lld
",ans);
    } 
    return 0;
}

T3 特技飞行

题意描述

公元 90129012 年，Z 市的航空基地计划举行一场特技飞行表演。表演的场地可以看作一个二维平面直角坐标系，其中横坐标代表着水平位置，纵坐标代表着飞行高度。

在最初的计划中，这 (n) 架飞机首先会飞行到起点 (x = x_{st}) 处，其中第 (i) 架飞机在起点处的高度为 (y_{i,0})。它们的目标是终点 (x = x_{ed}) 处，其中第 (i) 架飞机在终点处的高度应为 (y_{i,1})。因此，每架飞机可以看作坐标系中的一个点，它的航线是从 ((x_{st},y_{i,0})) 出发、到 ((x_{ed},y_{i,1})) 结束的一条线段，如下图所示。

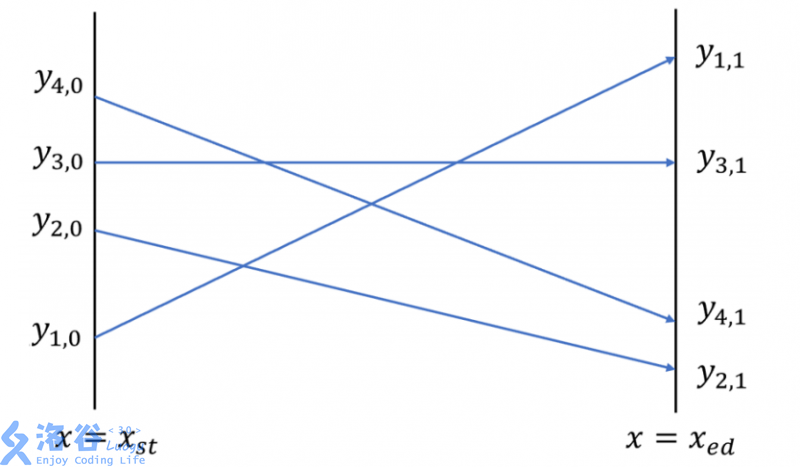
这 (n) 架飞机同时出发且始终保持一定的对地速度。因此，对于任意两条交叉的航线（线段），对应的两架飞机必然会同时到达交点处——这就是它们进行特技表演的时刻。它们将会偏转机翼，展现以极近的距离「擦身而过」特技，然后继续保持各自的航线。

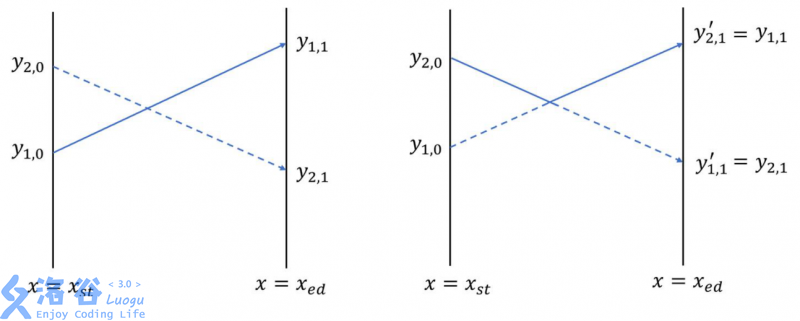
航空基地最近还研究了一种新的特技「对向交换」。当两架飞机到达交点处时，之前正在下降的那架立即转为执行抬升动作，之前正在上升的那架则执行一次空翻，两架飞机一上一下、机腹对机腹，同样以极近的距离经过交点，然后互相交换接下来的航线。

我们不必关心特技动作在物理上究竟是如何实现的，飞机仍然看作一个点，在两种特技动作下，航线的变化如下图所示 ((y_{i,1})) 表示交换航线后第 (i) 架飞机在终点的新高度）。容易发现，「对向交换」会使它们的航线变为折线，并保持它们在纵坐标上的相对顺序；而「擦身而过」会改变它们在纵坐标上的相对顺序。

现在，观看表演的嘉宾团提出了一个苛刻的要求——在终点 (x = x_{ed}) 处，按照高度排序，(n) 架飞机的相对顺序必须与 (x = x_{st}) 处的相对顺序一致。嘉宾团还给「对向交换」特技和「擦身而过」特技分别评定了难度系数 (a) 和 (b)，每次「对向交换」特技可以获得 (a) 的分数，每次「擦身而过」特技可以获得 (b) 的分数。

除此以外，嘉宾团共有 (k) 名成员，第 (i) 名成员会乘热气球停留在位置 ((p_i,q_i)) 处，具有 (r_i) 的观测距离，可以观测到区域 (|x - p_i| + |y - p_i| le r_i)∣ 里的所有特技。
若某个交点处的特技被一名或多名嘉宾观测到，则可以获得 (c) 的额外加分。
注意：特技无论是否被观测到，均可以获得 a 或者 b 的得分。

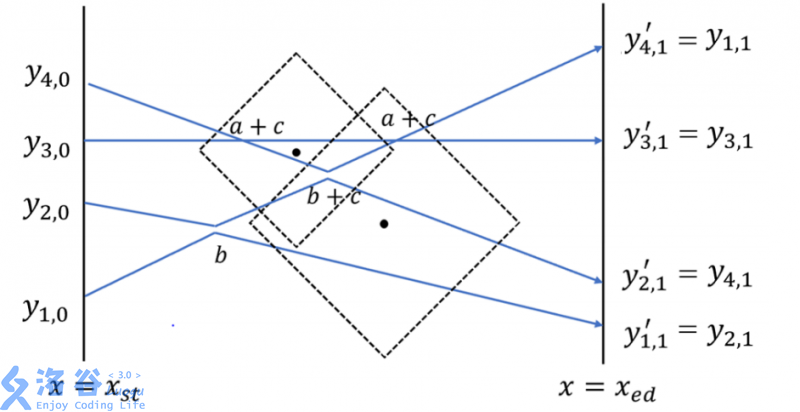
下图是对本题第一幅图 (4) 条航线 (4) 个交点的一种满足要求的安排，包括 (2) 次「对向交换」、(2) 次「擦身而过」，(3) 项特技被观测到，得分 (2a + 2b + 3c)。为了方便观察，图中展现「对向交换」特技的交点稍稍有些分离。

在这次的剧情里，你成为了 Z 市航空基地的规划员，你可以决定在每个交点处是执行「对向交换」还是「擦身而过」。你被要求在保证嘉宾团要求的前提下，计算整个特技表演的可能得到的最低和最高分数。

数据范围：(n,kleq 100000,交点数leq 500000)

solution

计算几何+扫描线。

去看洛谷题解吧，那里写的挺详细的。