一、四大基础理论
1 空间概率
空间概率是一种符合地理学第一定律的联合概率joint probabilities
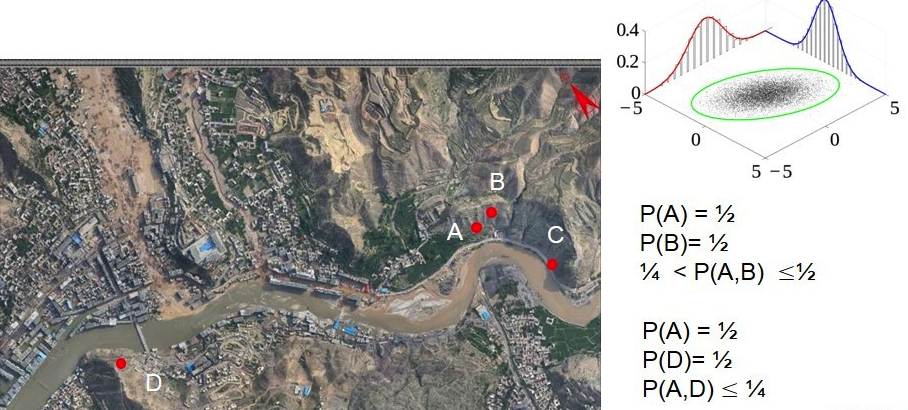
AB同时发生滑坡,比AD同时发生概率要高
2 概率密度(probability density)
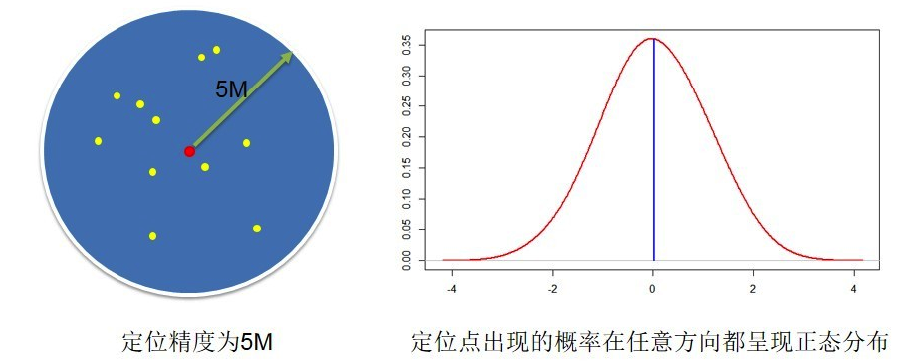
测量值的偏差在任意方向都会出现一定的散布,而散布的概率理论上会形成正态分布的对称曲线。在空间上可以把这个分布想象成一个钟形,那么任何一个事件在任意区域发生的概率,就是这个钟表面在这个区域上的所占的体积。
3 不确定性
不确定性可以传递— 数据的不确定性,最后肯定带来结果的不确定性。
了解数据中不确定性和研究这些不确定性如何影响分析结果是重中之重。
比如地统计学,采用随机过程来模拟插值的变异情况,就是不确定性研究的一项成果。

4 统计推断 (statistical inference)
其通过样本分析推理以求得到关于包括了样本在内的更大群体的结论。

空间统计与经典统计最大的不同点就在于要素之间的相关性,所以我们在做空间分析的时候,通常是在我们能够获得的所有数据上进行操作,因此很少或者更本没有一个用于提取数据并进行推理的总体概念。而且认为每个样本观测值是独立的观点也是不行的,除非相距很远。
所以空间分析很早就有了现在所谓的大数据分析的思路之一:总体分析,局部验证。
二、统计学主要内容
1 聚合- 整体性描述(Aggregation)
细节丰富但要有意识的抽象
常用的有众数、中位数和均值等
在空间统计的领域里面,也有各类概念来表达,比如对于数据分布的整体描述,空间自相关,对于数据之间的差异性,有空间异质性等等。
2 信息- 度量与变化(Information Measurement)
抽样过程中样本数量和对象的选择
但是在空间统计领域,因为空间自相关和空间异质性的存在,如何抽样就成了一个新的大问题——如何保证抽样出来的数据保有了原始数据的空间相关性和异质性,是一个大问题
3 似然- 概率尺度上的校准
似然度指的是在特定分布下出现的概率。具体指某件事在在限定的大背景下发生的概率。(贝叶斯概率?)
“传统世界观是决定论的、逻辑的,但统计世界观是概率的,不可知的或可更新的”
4 相互比较- 样本内的变异
有了面向背景目标的似然度,统计学可以解决外部比对问题,也就是跟预设分布去比较。然而,现实问题更多是数据内部的异质性所要求的内部比较,很多耳熟能详的统计方法例如 t 检验、方差分析、Bootstrap 等都是用来解决内部比较问题的。
5 回归- 多元分析、贝叶斯因果
事都会回归到本来的样子,规律性是松弛有度的。
空间统计里面,加入了地理加权回归。但实际中,更多是用来做方法比较,或是回归系数检验
6 设计- 实验方案与随机
7 残差- 科学逻辑与模型比较
本质上科学就是通过解释剩余现象进步,但是大家伙都在当前的噪音里探索未知信号的模式。具体到统计模型就是对模型解释不了的部分与模型诊断的思想
三、空间统计学
空间分布模式:通常指的是带有位置属性的数据在一定的空间范围内的分布规律
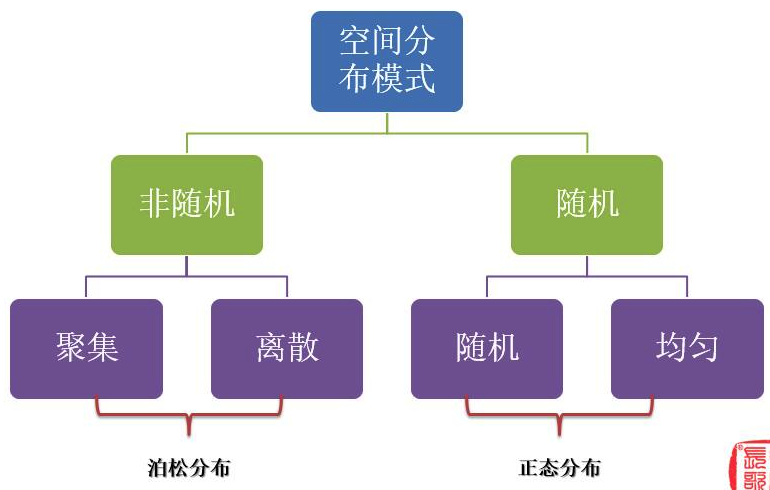
最开始采用样方分析,后来出现了很多空间自相关的指数,如莫兰指数,join count,Geary's C等。总之都是对一份数据进行全局性描述。
参考: