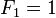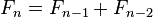最近在研究算法,遇到了斐波纳契函数,即1,2,3,5,8,13,21,34,55,89,...,通用式为:f(n)=f(n-1)+f(n-2).
在数学上,费波那西数列是以递归的方法来定义:
用文字来说,就是费波那西数列由 0 和 1 开始,之后的费波那西系数就由之前的两数相加。首几个费波那西系数是(OEIS A000045):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,………………
特别指出:0不是第一项,而是第零项。
摘自维基百科,斐波纳契数列
好了,题目来了:请用程序实现斐波纳契函数.
菜鸟的程序员想了想,画了个圈--不会.
一般的程序员想了想,撸起袖子,开工.
1 public static int fib(int n){ 2 if(n<=2){ 3 return 1; 4 }else{ 5 return fib(n-1)+fib(n-2); 6 } 7 }
高手的程序员想了又想,慎重的写下了:
1 public static int fibonacci(int n) { 2 3 if (n <= 2) { 4 return 1; 5 } 6 7 int result = 0; 8 int first = 0, second = 1; 9 10 for (int i = 1; i < n; i++) { 11 result = first + second; 12 first = second; 13 second = result; 14 } 15 16 return result; 17 }
前者使用的是递归,后者使用的是简单的循环.《数据结构与问题求解(Java语言版)(第4版)》中指出:
永远不要用递归代替简单的循环.
当然二者的实现都是正确的,不过我们现在所要关注的问题是:效率
假设C(N)是在计算fib(n)时fib函数总共被调用的次数,而C(0)=C(1)=1,那么:
C(N)=C(N-1)+C(N-2)+1,其中1是调用fib(n)的次数.
对于N≧3,C(N)=F(N+2)+F(N-1)-1.(该公式是归纳法推导得出,具体推导方式本人也不会,有知道的可以告诉在下).
根据公式,当N=40时,F(40)=102334155,而总递归次数为F(42)+F(39)-1=331160281,超过了3亿.
递归调用会导致冗余计算.例如,计算f(n)时,需要计算,f(n-1)和f(n-2),而计算f(n-1)时需要计算f(n-2)和f(n-3),重复计算了f(n-2),而这种重复计算会随着n的增加爆炸性的增长.故而,不推荐使用递归解决斐波纳契函数.
另,看到一篇好文章,引用过来.斐波那契数列算法分析