层次遍历
使用 BFS 进行层次遍历。不需要使用两个队列来分别存储当前层的节点和下一层的节点,因为在开始遍历一层的节点时,当前队列中的节点数就是当前层的节点数,只要控制遍历这么多节点数,就能保证这次遍历的都是当前层的节点。
BFS用队列和循环,没有用递归。
关于树的bfs和dfs看下面这篇文章,但是后面习题答案有不正确的比如111求最小深度一眼错,因为我之前也是这么错的
https://developer.51cto.com/art/202004/614590.htm
还有一篇博客可以看看
https://www.cnblogs.com/xiaolovewei/p/7763867.html
1. 一棵树每层节点的平均数
637. Average of Levels in Binary Tree (Easy)
没想法没思路。。
new队列又一次让我发晕。。。:(顶级接口)Collection-->Queue-->Deque-->LinkedList(实现类,但是同时也是List接口的实现类)或PriorityQueue(实现类)
https://www.cnblogs.com/cs-lcy/p/7392633.html
之前栈和队列专题怎么刷完就忘记。。。
解法一:BFS
最直观的思路,广度优先搜索,即层序遍历。
以层为单元,逐层循环,一次处理整层的顶点。
根结点入队后,只要队列不空,就记录队列中顶点的数量,此后仅对该数量的顶点出列,并将它们的子结点入列。
这样,每轮循环,队列中顶点的数量表示的就是当前层顶点的数量,计算层平均值即可。
class Solution { public List<Double> averageOfLevels(TreeNode root) { List<Double> res = new ArrayList<>(); Queue<TreeNode> q = new LinkedList<>(); q.add(root); while(!q.isEmpty())//判断每一层 { int sz = q.size();//充当了计数的作用 double sum = 0;
for(int i = 0; i < sz; i++)//队列内循环 拿出这一层父节点,每拿一个取一下值累加。加入下一层孩子们 { TreeNode cur = q.poll(); sum += cur.val; if(cur.left != null) q.add(cur.left); if(cur.right != null) q.add(cur.right); }
res.add(sum / sz); } return res; } }
解法二:DFS
递归的时候多使用一个参数记录当前层号。
同时,使用两个实例变量List,一个记录每层结点数,一个记录每层结点值之和。
每访问一个结点,就更新该层结点数与结点值之和。
递归结束后,通过结点值之和与结点数计算层平均值。

class Solution { private List<Double> ans; private List<Integer> sz; public List<Double> averageOfLevels(TreeNode root) { ans = new LinkedList<>(); sz = new LinkedList<>(); dfs(root, 1);//层号从1开始 for(int i = 0; i < ans.size(); i++) ans.set(i, ans.get(i) / sz.get(i)); return ans; } private void dfs(TreeNode root, int layer) { if(root == null) return; if(sz. size() < layer)//意味着第一次到达该层 { sz.add(1); ans.add((double)root.val); } else { sz.set(layer-1, sz.get(layer-1) + 1); ans.set(layer-1, 1.0 * ans.get(layer-1) + root.val); } dfs(root.left, layer + 1); dfs(root.right, layer + 1); } } 作者:tyanyonecancode 链接:https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/solution/marveljian-dan-de-xue-xi-bi-ji-637-by-tyanyonecanc/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2. 得到左下角的节点
513. Find Bottom Left Tree Value (Easy)
给定一个二叉树,在树的最后一行找到最左边的值。
Input:
1
/
2 3
/ /
4 5 6
/
7
Output:
7
思路:最下一层第1个出队的结点的值
每层用不同队列?或者是非最后一层则清空队列?哦哦哦上一题就是!for循环清空队列!再加入!但最后一层也清空了才出while循环。
如何保证最后一行不被清空呢?
看答案。。
答案其实很简单,我的思路复杂了。。
答案根本没考虑每层要清多少这个问题,所以循环根本不需要,而是只要保证最下层左边第一个是最后一个加入队列的,那么while循环结束之前那个最后出来的,就是他了。
如何保证最后一个poll的是最下层最左,即再加入的时候,都先加右子树就好了嘛。。左右镜像思维一下。。
使用 BFS (广度优先搜索)进行层次遍历。创建一个队列来存放TreeNode。首先放入root节点。如果该队列不为空,则将最先放进去的节点设置为root并弹出,并且在队列中加入它的两个孩子节点。
先放右孩子节点,再放左孩子节点,这样就可以保证左边的节点永远在最后遍历,最后得到的就是最下面一层最左边的节点。
class Solution { public int findBottomLeftValue(TreeNode root) {
}
}
前中后序遍历
1
/
2 3
/
4 5 6
- 层次遍历顺序:[1 2 3 4 5 6]
- 前序遍历顺序:[1 2 4 5 3 6]
- 中序遍历顺序:[4 2 5 1 3 6]
- 后序遍历顺序:[4 5 2 6 3 1]
层次遍历使用 BFS 实现,利用的就是 BFS 一层一层遍历的特性;而前序、中序、后序遍历利用了 DFS 实现。
前序、中序、后序遍只是在对节点访问的顺序有一点不同,其它都相同。
① 前序 根左右
void dfs(TreeNode root) {
visit(root);
dfs(root.left);
dfs(root.right);
}
② 中序 左根右
void dfs(TreeNode root) {
dfs(root.left);
visit(root);
dfs(root.right);
}
③ 后序 左右根 (昨天的题好像挺多后序遍历最后才输出
void dfs(TreeNode root) {
dfs(root.left);
dfs(root.right);
visit(root);
}
1. 非递归实现二叉树的前序遍历
144. Binary Tree Preorder Traversal (Medium)
给定一个二叉树,返回它的 前序 遍历。
递归实现:
class Solution { public List<Integer> res = new ArrayList<>(); public List<Integer> preorderTraversal(TreeNode root) { if(root==null) return res; res.add(root.val); preorderTraversal(root.left); preorderTraversal(root.right); return res; } }
非递归,迭代实现需要用栈:
首先将根节点push入栈。
在循环体中,我们首先将栈顶元素pop出来存起来作为当前节点,将其值输出。然后先push它的右节点,再push它的左节点入栈,再进行下一轮循环。由于栈是后进先出,这样就保证先输出它的左节点。(有点像前面的513)
class Solution { public List<Integer> preorderTraversal(TreeNode root) { List <Integer> list = new ArrayList<>(); Stack <TreeNode> stack = new Stack<>(); stack.push(root); while(!stack.isEmpty()){ TreeNode node = stack.pop(); if(node==null) continue;//为null时跳过本次循环剩下的部分直接进入下一次循环 list.add(node.val); stack.push(node.right); stack.push(node.left); } return list; } }
2. 非递归实现二叉树的后序遍历
145. Binary Tree Postorder Traversal (Medium)
前序遍历为 root -> left -> right,后序遍历为 left -> right -> root。可以修改前序遍历成为 root -> right -> left,那么这个顺序就和后序遍历正好相反。
递归:
class Solution { public List<Integer> res = new ArrayList<>(); public List<Integer> postorderTraversal(TreeNode root) { if(root==null) return res; postorderTraversal(root.left); postorderTraversal(root.right); res.add(root.val); return res; } }
非递归,迭代:
前序遍历为:根左右,将其代码中左右push位置交换,变为根右左。然后最后倒序一下,即为左右根,就完成了后序遍历。
emmmm妙啊 根本没想到。。
class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> list = new ArrayList<>(); Stack<TreeNode> stack = new Stack<>(); stack.add(root); while(!stack.isEmpty()){ TreeNode node = stack.pop(); if (node == null) continue; list.add(node.val); stack.push(node.left); stack.push(node.right);//后进后出 } Collections.reverse(list); return list; } }
3. 非递归实现二叉树的中序遍历
94. Binary Tree Inorder Traversal (Medium)
递归:
class Solution { public List<Integer> res = new ArrayList<>(); public List<Integer> inorderTraversal(TreeNode root) { if(root==null) return res; inorderTraversal(root.left); res.add(root.val); inorderTraversal(root.right); return res; } }
非递归:
不能在循环中首先出栈root了。
不会啊。。。看答案。。
定义一个当前节点cur。先把root赋值给cur为初始值。
如果当前节点不为null,就将其push入栈,然后将cur移动到他的左子节点。再重新判断是否为null。
当前节点已经为null,则将栈顶元素push出来(null的父节点)输出,这样子输出的总是刚放进去的左子们,最后是root第一个放进去的(先左再根)。然后转向null的父节点的右子节点。(最后右)
public class Solution { public List < Integer > inorderTraversal(TreeNode root) { List < Integer > res = new ArrayList < > (); Stack < TreeNode > stack = new Stack < > (); TreeNode cur = root; while (cur != null || !stack.isEmpty()) { while (curr != null) { stack.push(curr); cur = cur.left; } cur = stack.pop(); res.add(cur.val); cur = cur.right; } return res; } }
中序遍历就是这样,有点难理解,看答案动图演示:

首先curr一路入栈左移到4,4没有左子,4出栈值被list加入,4没有右子此时cur=null了。由于栈不为空还是可以进入循环,由于cur此时为null,所以跳到下面把2出栈,cur变为2的右子5了。

又开始内循环栈中加入5,cur变为5的左子null,出了内循环往下5出栈进入res,此时5拿了刚刚4的剧本,cur为5的右子右为null了。由于栈中还有1所以可以进入外循环,1拿了2的剧本,跳过内循环被逼出来了。cur现在传到了3,3传给6 ,6先出再3出。。。
理解都很难了代码咋写的出来。。
我先跳了。。。
---------------------------------------------------------------------------------------------------------------
BST
二叉查找树(BST):根节点大于等于左子树所有节点,小于等于右子树所有节点。(若只有3个结点则左小于根,根小于右
二叉查找树中序遍历有序:用中序遍历来遍历二叉查找树,得到的数字是升序的(做题十分有用!)
(二叉查找树) 题6-题15
BST是满足如下3个条件的二叉树:
1. 节点的左子树包含的节点的值小于该节点的值
2. 节点的右子树包含的节点的值大于等于该节点的值
3. 节点的左子树和右子树也都是BST
BST的初始构建可以利用插入操作完成。BST最常使用的操作是查找和遍历,还有删除操作但相对较少使用。
1. 修剪二叉查找树
669. Trim a Binary Search Tree (Easy)
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
Input:
3
/
0 4
2
/
1
L = 1
R = 3
Output:
3
/
2
/
1
题目描述:只保留值在 L ~ R 之间的节点
需要遍历,然后剔除多余的,怎么写呢。。?
答案:应该用递归,多余的写到条件里。
题目要求返回BST被修剪后的根结点,那么我们从根结点开始修剪。
如果根结点太小,根结点的左子树的所有结点只会更小,说明根结点及其左子树都应该剪掉,因此直接返回右子树的修剪结果。
如果根结点太大,根结点的右子树的所有结点只会更大,说明根结点及其右子树都应该剪掉,因此直接返回左子树的修剪结果。
如果根结点没问题,则递归地修剪左子结点和右子结点。
如果结点为空,说明无需修剪,直接返回空即可。
左右子结点都修剪完后,返回自身。
class Solution { public TreeNode trimBST(TreeNode root, int L, int R) { if(root == null) return null; if(root.val < L) return trimBST(root.right, L, R); if(root.val > R) return trimBST(root.left, L, R);
//上面只是条件 下面才是真正的方法内容 内容就是递归 root.left = trimBST(root.left, L, R); root.right = trimBST(root.right, L, R); return root; } } 作者:tyanyonecancode 链接:https://leetcode-cn.com/problems/trim-a-binary-search-tree/solution/marveljian-dan-de-xue-xi-bi-ji-669-by-tyanyonecanc/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
为什么想不到这样做。。。
2. 寻找二叉查找树的第 k 个元素
230. Kth Smallest Element in a BST (Medium)
这里是二叉查找树,用中序遍历可以从小到大排序取出值。把中序遍历中间那个打印步骤改为计数,也就是没有左子的就返回记个数,再去看他的右子。
中序遍历解法:
private int cnt = 0; private int val; public int kthSmallest(TreeNode root, int k) { inOrder(root, k); return val; } private void inOrder(TreeNode node, int k) { if (node == null) return; inOrder(node.left, k);//左 cnt++; if (cnt == k) { val = node.val; return; } inOrder(node.right, k);//右 }
671可不可以也这样做?671就是前序遍历可以从小到大打印出来。。用递归然后我晕掉了。
emmmm我天真了,671是要求值为第二位,而不是排在第二位的元素的值。比如最小的有2个2,第二小的是排在第3位的5。。。
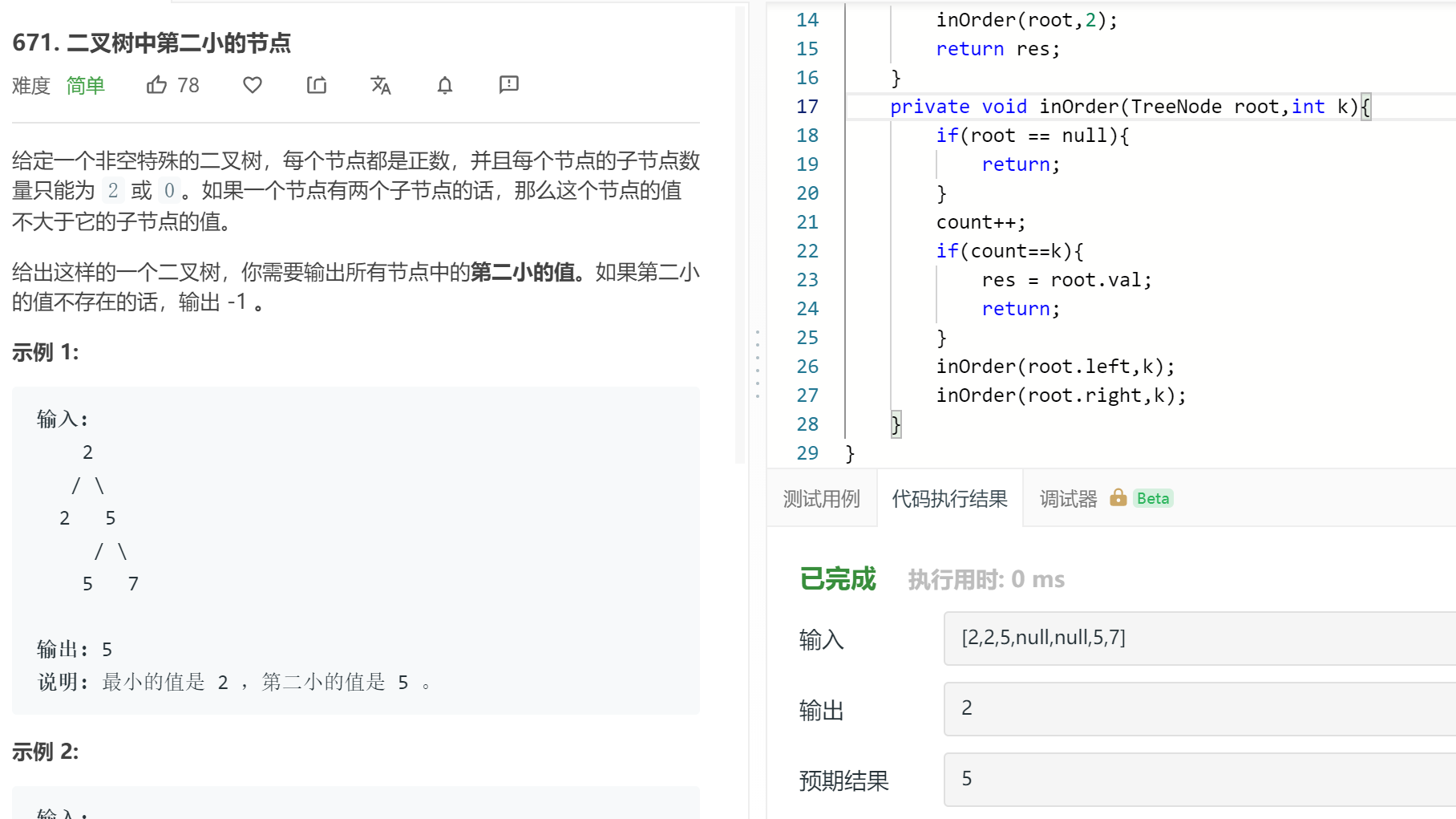
671正确解法见上一篇博客。。。
好吧我们回到这一题的迭代解法:
先写一个count()方法用来计算已当前节点为root的树的节点数。
在主方法中,我们定义一个leftcount变量来计算该树左子树的节点数。然后分3种情况讨论:
1.因为左子树所有节点的值都小于root节点,所以如果leftcount==k-1,说明root就是第k小的那个节点。
2.如果leftcount>k-1,说明第k小的节点在左子树中,递归返回左子树的第k小的节点(不用管原来的root了和root.right了。此时root.left就是root,找第k小没变,所以可以用递归)。
3.如果leftcount<k-1,说明第k小的节点在右子树中,递归返回右子树的第k-leftcount-1小的节点(同上)。
class Solution {
public int kthSmallest(TreeNode root, int k) { int leftcount = count(root.left); if(leftcount==k-1) return root.val; if(leftcount>k-1) return kthSmallest(root.left,k); return kthSmallest(root.right,k - leftcount - 1); } private int count(TreeNode root){ if(root==null) return 0;
return 1+count(root.left)+count(root.right); } }
3. 把二叉查找树每个节点的值都加上比它大的节点的值
538:Convert BST to Greater Tree (Easy)
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
Input: The root of a Binary Search Tree like this:
5
/
2 13
Output: The root of a Greater Tree like this:
18
/
20 13
先遍历右子树。
其实和230差不多,就左和右顺序互换一下,然后230是计数,这里是累加:
class Solution { private int sum = 0; public TreeNode convertBST(TreeNode root) { if(root == null){ return null; } inOrder(root); return root; } private void inOrder(TreeNode node){ if(node == null){ return; } inOrder(node.right);//先右 sum+=node.val; node.val = sum; inOrder(node.left);//后左 } }
中序遍历的镜像
4. 二叉查找树的最近公共祖先
235. Lowest Common Ancestor of a Binary Search Tree (Easy)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
这是简单题??感觉好难。。没有想法。。
答案竟然三行代码解决。。。充分利用了二叉查找树的性质
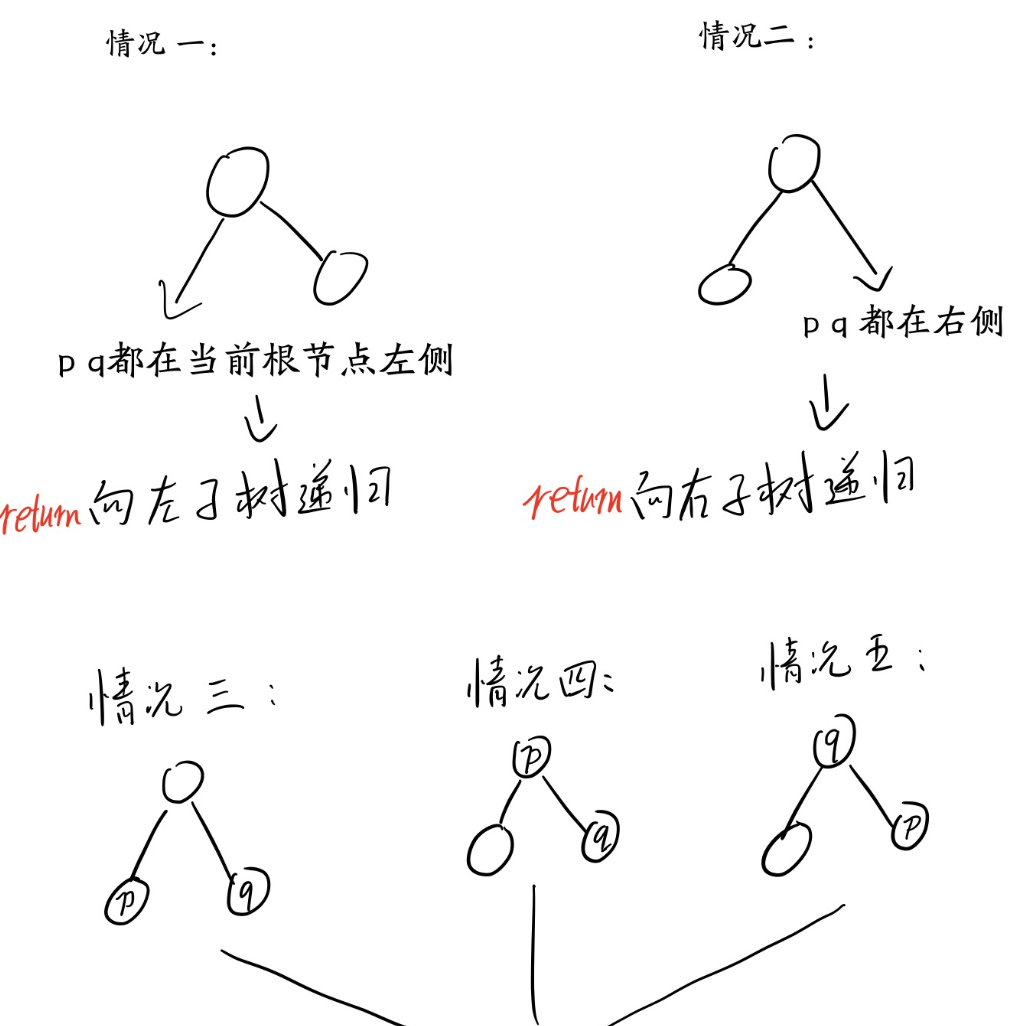
情况三,四,五 都是直接 return root 就是
情况1(情况2同理):

情况3,4,5:
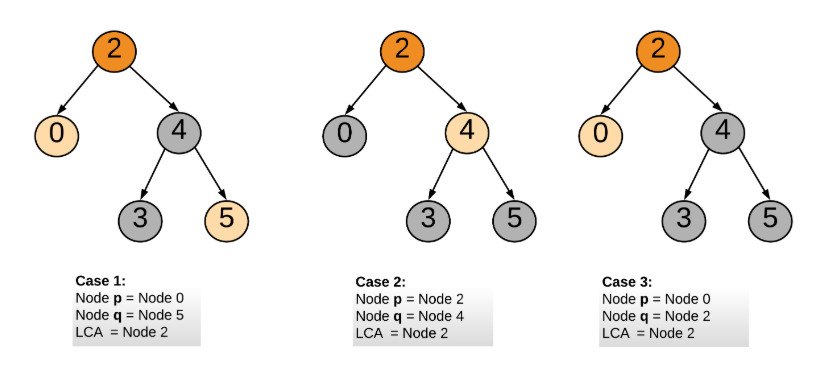
所以:
class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if(root.val>p.val && root.val>q.val) return lowestCommonAncestor(root.left, p, q);//p,q都在左子树,root.left视为新root if(root.val<p.val && root.val<q.val) return lowestCommonAncestor(root.right,p,q);//p,q都在右子树,root.right视为新root return root; } } 作者:get996 链接:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/solution/javadi-gui-san-xing-dai-ma-by-get996/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
5. 二叉树的最近公共祖先
236. Lowest Common Ancestor of a Binary Tree (Medium)
情况还是一样。。但是没有二叉查找树那么方便写判断条件。。
想不出来。。。
看答案:
啊 就是普通的分情况递归,有递归终点和递归体,根据不同情况各有各的返回值。
看了半个多小时终于明白了,我纠结的最底层或底层的return 了东西,程序为啥没结束这个问题。。。因为!!底层的return 只返回给上一层!!根本还没出那一行代码呢!要到最外层,才是真正的return!!!!!!!(把这里的return跟之前的打印搞混了。。。)
过程就是类似后序遍历
终止条件:当越过叶节点,或当 root等于 p或q,则直接返回 root;(底层只返回给上一层。。。就是当前递归方法返回值。。)
递归体:
开启递归左子节点,返回值记为 left;
开启递归右子节点,返回值记为 right;
根据 left 和 right ,可展开为四种情况;
1.当 left和 right同时为空 :说明 root的左 / 右子树中都不包含 p,q,返回 null;
2.当 left和 right同时不为空 :说明 p, q分列在 root 的 异侧 ,因此 root 为最近公共祖先,返回 root ;
3.当 left为空 ,right不为空 :p,q 都不在 root的左子树中,直接返回 right。具体可分为两种情况:
p,q 其中一个在 root的 右子树 中,此时 right指向 p(假设为 p );(q可能在右子树的上一层也是在右边还没找到??)
p,q 两节点都在 root的 右子树 中,此时的 right指向 最近公共祖先节点 ;
4.当 left不为空 ,right为空 :与情况3同理;
看解析动图理解过程
class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if(root==null||root==p||root==q) return root;
//然后是分别对左子树 和 右子树 去找返回值去了 找到以后递归出到根下面那一层 就能拿到之前他们业作为根时拿到的返回值 此时可以返回给主方法了 TreeNode left = lowestCommonAncestor(root.left,p,q); TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left==null && right==null) return null; if(left == null) return right; if(right == null) return left; return root; } }
虽然但是。。。好难啊。。。这能想到咩
6. 从有序数组中构造二叉查找树
108. Convert Sorted Array to Binary Search Tree (Easy)
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
emmmm依然没有想法。。高度差有一题DFS做过,就是dfs左-右?递归树110题判断是否是平衡树。
看答案:
解法一 递归
如果做了 98 题 和 99 题,那么又看到这里的升序数组,然后应该会想到一个点,二叉搜索树的中序遍历刚好可以输出一个升序数组。
所以题目给出的升序数组就是二叉搜索树的中序遍历。
根据中序遍历还原一颗树,又想到了 105 题 和 106 题,通过中序遍历加前序遍历或者中序遍历加后序遍历来还原一棵树。前序(后序)遍历的作用呢?提供根节点!然后根据根节点,就可以递归的生成左右子树。
这里的话怎么知道根节点呢?平衡二叉树,既然要做到平衡,我们只要把根节点选为数组的中点即可。(因为前后都是排好序的)
综上,和之前一样,找到了根节点,然后把数组一分为二,进入递归即可。注意这里的边界情况,包括左边界,不包括右边界。
class Solution { int[] nums; public TreeNode helper(int left, int right) { if (left > right) return null;//递归终点 // always choose left middle node as a root int p = (left + right) / 2;//中点是每个递归自己更新的 // inorder traversal: left -> node -> right TreeNode root = new TreeNode(nums[p]);//这是根结点选为数组中点的意思 (为什么IDEA上这样不行啊? root.left = helper(left, p - 1);//左节点为左边一半的中心 (把它当作root递归)(这是赋值,因为helper方法会return root) root.right = helper(p + 1, right);//右节点为右边一半的中心 (同上 return root;//最外层返回的root才是传到主方法的 } public TreeNode sortedArrayToBST(int[] nums) { this.nums = nums; return helper(0, nums.length - 1); } } 作者:LeetCode 链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-15/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
啊啊啊啊好难啊
这题答案不是唯一的,与预期不同也能AC
7. 根据有序链表构造平衡的二叉查找树
109. Convert Sorted List to Binary Search Tree (Medium)
Given the sorted linked list: [-10,-3,0,5,9],
One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:
0
/
-3 9
/ /
-10 5
这哪里会啊 把不符合的指针都打断吗。。
答案:
和上一题一样,当前方法和下一个方法的主要思路是:
给定列表中的中间元素将会作为二叉搜索树的根,该点左侧的所有元素递归的去构造左子树,同理右侧的元素构造右子树。这必然能够保证最后构造出的二叉搜索树是平衡的。
算法
- 由于我们得到的是一个有序链表而不是数组,我们不能直接使用下标来访问元素。我们需要知道链表中的中间元素。(对,我没想到要怎么解决啊)
-
我们可以利用两个指针来访问链表中的中间元素。假设我们有两个指针 slow_ptr 和 fast_ptr。slow_ptr 每次向后移动一个节点而 fast_ptr 每次移动两个节点。当 fast_ptr 到链表的末尾时 slow_ptr 就访问到链表的中间元素。对于一个偶数长度的数组,中间两个元素都可用来作二叉搜索树的根。(原来如此,关于链表找中间元素是使用快慢指针!)
-
当找到链表中的中间元素后,我们将链表从中间元素的左侧断开(因为中间元素不用参与,是根结点的赋值),做法是使用一个 prev_ptr 的指针记录 slow_ptr 之前的元素,也就是满足 prev_ptr.next = slow_ptr。断开左侧部分就是让 prev_ptr.next = None。
-
我们只需要将链表的头指针传递给转换函数,进行高度平衡二叉搜索树的转换。所以递归调用的时候,左半部分我们传递原始的头指针;右半部分传递 slow_ptr.next 作为头指针。
class Solution { private ListNode findMiddleElement(ListNode head) { // The pointer used to disconnect the left half from the mid node. ListNode prevPtr = null; ListNode slowPtr = head; ListNode fastPtr = head; // Iterate until fastPr doesn't reach the end of the linked list. while (fastPtr != null && fastPtr.next != null) {//循环给3个指针赋值 prevPtr = slowPtr; slowPtr = slowPtr.next; fastPtr = fastPtr.next.next; } // Handling the case when slowPtr was equal to head. if (prevPtr != null) {//赋值结束后pre已经是slow即中间元素的上一步 prevPtr.next = null;//从中间元素左侧断开,此时初始链表head已经只剩一半了,另一半是slowPtr.next开头的链表 } return slowPtr;//最后返回中间元素结点 } public TreeNode sortedListToBST(ListNode head) { // If the head doesn't exist, then the linked list is empty if (head == null) { return null; } // Find the middle element for the list. ListNode mid = this.findMiddleElement(head); // The mid becomes the root of the BST. TreeNode node = new TreeNode(mid.val); // Base case when there is just one element in the linked list if (head == mid) { return node; } // Recursively form balanced BSTs using the left and right halves of the original list. node.left = this.sortedListToBST(head); node.right = this.sortedListToBST(mid.next); return node;//最终是拿到最外层返回的Treenode } } 作者:LeetCode 链接:https://leetcode-cn.com/problems/convert-sorted-list-to-binary-search-tree/solution/you-xu-lian-biao-zhuan-huan-er-cha-sou-suo-shu-by-/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
It's too hard for me...
8. 在二叉查找树中寻找两个节点,使它们的和为一个给定值
653. Two Sum IV - Input is a BST (Easy)
Input:
5
/
3 6
/
2 4 7
Target = 9
Output: True
使用中序遍历得到有序数组之后,再利用双指针对数组进行查找。
应该注意到,这一题不能用分别在左右子树两部分来处理这种思想,因为两个待求的节点可能分别在左右子树中。
public boolean findTarget(TreeNode root, int k) { List<Integer> nums = new ArrayList<>(); inOrder(root, nums); int i = 0, j = nums.size() - 1; while (i < j) { int sum = nums.get(i) + nums.get(j); if (sum == k) return true; if (sum < k) i++; else j--; } return false; } private void inOrder(TreeNode root, List<Integer> nums) { if (root == null) return; inOrder(root.left, nums); nums.add(root.val);//这里如果是数组的话就不方便添加元素了,因为数组不可变长度,是初始化就定义好的 inOrder(root.right, nums); }
数组res也必须是new ArrayList才行。不可以只声明不新建。(卡半天不知道哪里错。。。
class Solution { List<Integer> res = new ArrayList<>(); public boolean findTarget(TreeNode root, int k) { List<Integer> list = new ArrayList<>(); list = inOrder(root); int i = 0, j = list.size() - 1; while (i < j) { int sum = list.get(i) + list.get(j);//天呐我用成list[i]+list[j]...这不是数组注意!!!! if (sum == k) return true; if (sum < k) i++; else j--; } return false; } private List<Integer> inOrder(TreeNode root){ if(root==null){ return null; } inOrder(root.left); res.add(root.val);//这里如果是数组的话就不方便添加元素了,因为数组不可变长度,是初始化就定义好的
inOrder(root.right);
return res; }
}
不一定非要返回值也可以取到的,比如前面答案作为参数,后面一题直接设为全局变量就可以直接取了。
感觉我还没搞明白全局变量局部变量,参数和返回值到底该怎么设置。。。
9. 在二叉查找树中查找两个节点之差的最小绝对值
530. Minimum Absolute Difference in BST (Easy)
Input:
1
3
/
2
Output:
1
利用二叉查找树的中序遍历为有序的性质,计算中序遍历中临近的两个节点之差的绝对值,取最小值。
不是list里面的前两个,而是所有相邻的差值比较一下。min=Math.min(res,min)
我的想法是和上面一题一样先搞个list存,然后嵌套着比。错了呜呜呜也不知道哪里错了。。。
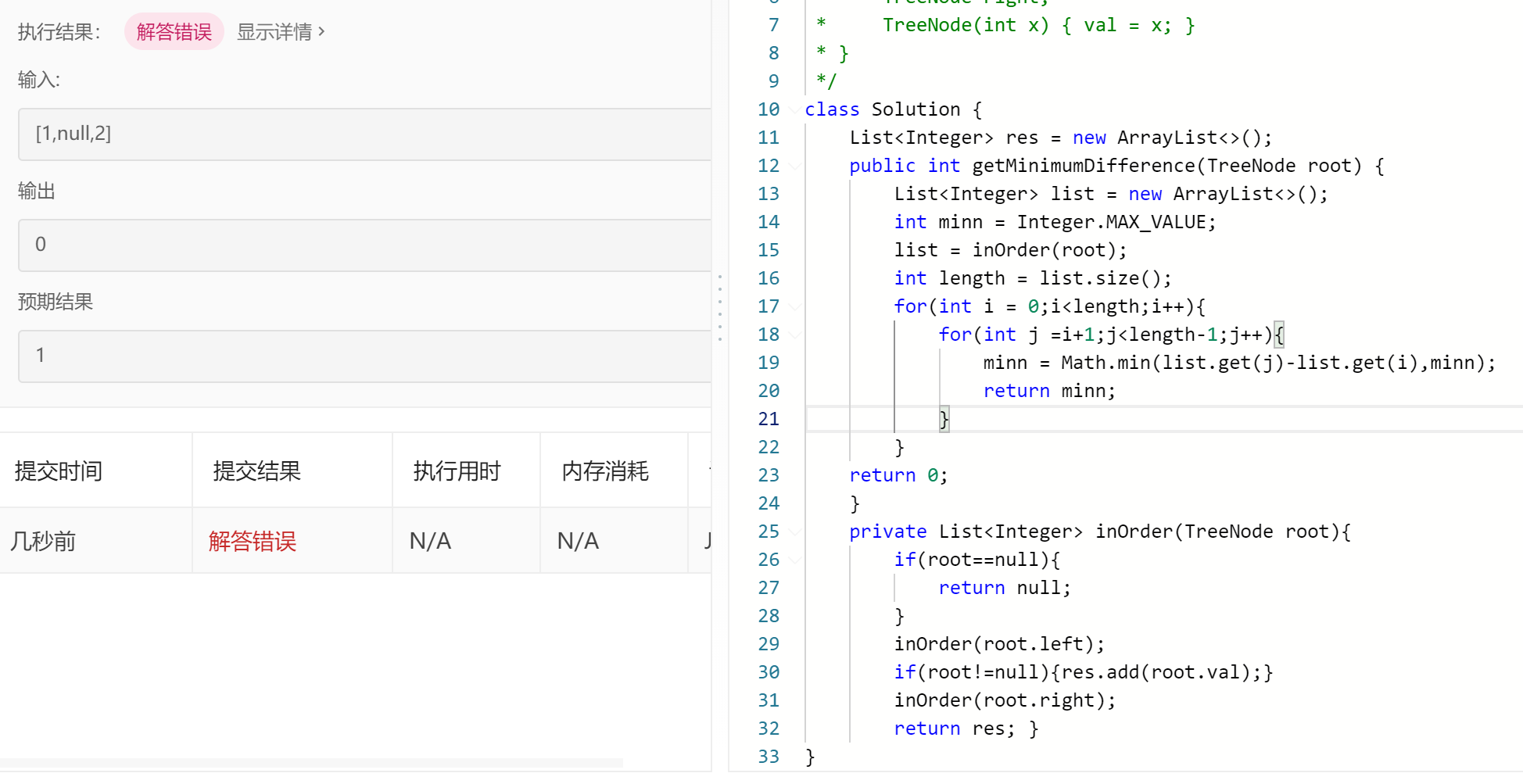
怎么debug啊呜呜呜
答案:在中序遍历时就找到minn了,我上面思路异于常人多此一举。。。
在中序遍历的过程中,在遍历右节点之前,保存好上次的当前节点。在遍历了左节点后,将当前节点与上一个当前节点作差,并更新最小差值minDiff。
注意:初始化minDiff时,要将其初值设置为一个非常大的数,MAX.VALUE。否则,万一最小差值比设定的初值还要大,那么midDiff就恒为初值了。
private int minDiff = Integer.MAX_VALUE; private TreeNode preNode = null; public int getMinimumDifference(TreeNode root) { inOrder(root); return minDiff; } private void inOrder(TreeNode node) { if (node == null) return; inOrder(node.left); if (preNode != null) minDiff = Math.min(minDiff, node.val - preNode.val);//不断更新最小绝对值minDiff
preNode = node; //上面这个减法 这里node和pre就是相邻的结点 但是node比pre大因为到这里node是右边的了 pre是根(对吗?)
inOrder(node.right);
}
10. 寻找二叉查找树中出现次数最多的值
501. Find Mode in Binary Search Tree (Easy)
1
2
/
2
return [2].
答案可能不止一个,也就是有多个值出现的次数一样多。
这个应该用map装值和次数吧我记得。(但是这样做差点超时了。。。。)
class Solution { public int[] findMode(TreeNode root) { if (root == null) return new int[0];//这个没写导致一直没通过 List<Integer> nums = new ArrayList<>(); inOrder(root, nums); Map < Integer, Integer > map = new HashMap<>(); List<Integer> help = new ArrayList<>(); for(int n:nums){ map.put(n, map.getOrDefault(n, 0) + 1); } int degree = Collections.max(map.values());//某个出现最多的元素的出现次数 for (int x: map.keySet()) {//遍历键们(键是存的数组的元素,所以这里遍历数组也一样 但这个比数组元素少因为重复的元素作为键只能存一次 if (map.get(x) == degree) {//找到x为度对应的元素值!!! help.add(x);//存的得是元素值而不是出现次数!!!!!!!!!!!!!!!!!! } } //把help中的数放到list中去(题目返回格式要求)list转数组 int[] list = new int[help.size()]; int idx=0; for(int num:help){ list[idx++]= num; } return list; } private void inOrder(TreeNode root, List<Integer> nums) { if (root == null) return; inOrder(root.left, nums); nums.add(root.val);//这里如果是数组的话就不方便添加元素了,因为数组不可变长度,是初始化就定义好的 inOrder(root.right, nums); } }
答案有更好的解法:
思路分析:
找众数,说明要统计出现次数,一般会直接想到搞个哈希表来计数(就像后面的方法二)。但是如果一个有序数组中统计出现次数,使用双指针就能很好解决,类似的这里给我们的树不是一般的树,而是BST,中序遍历相当于遍历有序数组。
利用BST这个特性,我们不需要使用哈希表来计数。如同双指针的做法,这里也需要记录上一个结点TreeNode pre;这样才能知道当前结点值与谁比较;另外还需要记录某个值的出现次数curCount,以及出现次数的最大值maxCount(否则你咋知道谁出现最多次)。并且这里遍历过程中的众数信息需要记录(List存放众数)及更新。
在中序遍历中:(在中序遍历中就要开始处理了!!)
如果pre == null,说明这是遍历的第一个结点,不需要处理(第一个结点的初条件在主函数中设定)。
如果当前结点值与上一个结点值相等,那么这个数字的出现次数+1。
否则,我们先去判断,上一个数字的出现次数curCount与之前的最大出现次数maxCount谁更大:
如果上一个数字出现次数最大,需要更新众数信息。首先更新最大出现次数maxCount = curCount;。然后将之前记录的众数清空,再将上一个数字放入items.clear(); items.add(pre.val);
如果一个数字出现次数等于最大出现次数,那么目前来看,它也是可能的众数,加入列表items.add(pre.val);
否则,上一个数字一定不是众数,不管它,继续保留List中的数字。
最后,重置计数curCount = 1;,表示当前数字出现一次了。
然后更新pre = x;
回到主函数:
特殊情况处理,root == null直接返回new int[0]。
然后上文提到的初始化,因为最左边结点在中序的递归中不处理,所以,我们要首先将maxCount = 1,因为树非空总会有数字出现一次,然后curCount = 1,代表最左边结点被我们在主函数计数了。
调用辅助函数后,还需要处理最后一个结点的值,因为在递归中不会有再下一个结点值与之不相等然后来判断它的值是否为众数。
所以如果curCount > maxCount,说明最后一个结点才是唯一众数,return new int[]{pre.val};
如果curCount == maxCount,说明最后一个结点也是众数,items.add(pre.val);
最后,将List转成数组返回。
这个题要注意边界的考虑!
private List<Integer> items; private int maxCount; private int curCount; private TreeNode pre; public int[] findMode(TreeNode root) { if (root == null) return new int[0]; items = new ArrayList<>(); // 这里设置为1是因为 在递归中 BST中最左边的结点被跳过了,作为初状态 该结点值出现一次,记录的出现最多次数一开始也为1 maxCount = 1; curCount = 1; midTraversal(root); // 最右端结点的处理,从递归中看,最后一个结点与前一个结点相等只更新了curCount的值;不相等则只考虑到倒数第二个结点。 if(curCount > maxCount) return new int[]{pre.val}; if(curCount == maxCount) items.add(pre.val); int[] res = new int[items.size()]; for (int i = 0; i < res.length; i++) res[i] = items.get(i); return res; } private void midTraversal(TreeNode x) { if (x == null) return; midTraversal(x.left); if(pre != null){ if(x.val != pre.val){ // 说明上一个值的结点数量已经统计完成 要看出现次数的情况 if(curCount > maxCount){ // 出现次数更多,清空之前的出现少的数,更新最大出现次数 maxCount = curCount; items.clear(); items.add(pre.val); } else if(curCount == maxCount){ // 不止一个众数 items.add(pre.val); } curCount = 1; // 当前值与上一个结点值不同,重置计数 } else curCount++; // 当前值与上一个结点值相同,当前值的出现次数增加。 } pre = x; midTraversal(x.right); }
作者:ustcyyw
链接:https://leetcode-cn.com/problems/find-mode-in-binary-search-tree/solution/501javazhong-xu-bian-li-chang-shu-kong-jian-xiang-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
心累。。。有空再来研究这个方法的代码吧先跳了。。。
Trie(发音为try)
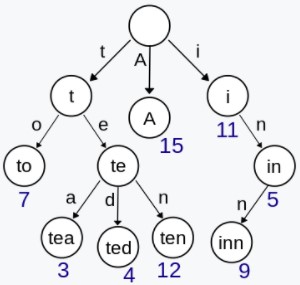
Trie,又称前缀树或字典树,用于判断字符串是否存在或者是否具有某种字符串前缀。
又称单词查找树,Trie树,是一种树形结构。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
1. 实现一个 Trie
208. Implement Trie (Prefix Tree) (Medium)
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true
-----------------------------------------------------------------------------------------------------------------------------------
介绍 Trie
Trie 是一颗非典型的多叉树模型,多叉好理解,即每个结点的分支数量可能为多个。
为什么说非典型呢?因为它和一般的多叉树不一样,尤其在结点的数据结构设计上,比如一般的多叉树的结点是这样的:
struct TreeNode {
VALUETYPE value; //结点值
TreeNode* children[NUM]; //指向孩子结点
};
而 Trie 的结点是这样的(假设只包含'a'~'z'中的字符):
struct TrieNode {
boolean isEnd; //该结点是否是一个串的结束
TrieNode* next[26]; //字母映射表
};
要想学会 Trie 就得先明白它的结点设计。我们可以看到TrieNode结点中并没有直接保存字符值的数据成员,那它是怎么保存字符的呢?
用于敏感词过滤。。。
看不懂。。头晕。。。
https://blog.csdn.net/u013309870/article/details/71081393
2. 实现一个 Trie,用来求前缀和
677. Map Sum Pairs (Medium)