欧拉函数:
就是对于一个正整数n,小于n且和n互质的正整数(包括1)的个数,记作φ(n) 。欧拉函数的通式:φ(n)=n*(1-1/p1)(1-1/p2)(1-1/p3)*(1-1/p4)……(1-1/pn),其中p1, p2……pn为n的所有质因数,n是不为0的整数。φ(1)=1(唯一和1互质的数就是1本身)。
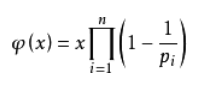
关于欧拉函数有如下几点性质:
1、phi(1) = 1
2、若n是质数,那么phi(n) = n-1
3、若n是质数x的k次幂,phi(n) = (x-1)*x^(k-1)
4、若m,n互质,那么phi(m*n) = phi(m)*phi(n)
5、若n是奇数,那么phi(2*n) = phi(n)
6、若x,y是质数,且n = x*y,那么phi(n) = (x-1)*(y-1)
6、小于n且与n互质的数的和为:n/2 * phi(n)
7、b mod a = 0, phi[a*b]=phi[b]*a
可以得到一个在分解质因数时同时求解单个欧拉函数的方法

1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 int main() { 5 int n, ans; 6 cin >> n; 7 ans = n; 8 for (int i = 2; i * i <= n; ++i) 9 if (n % i == 0) 10 { 11 ans = ans / i * (i - 1); 12 while (n % i == 0) 13 n /= i; 14 } 15 if (n > 1) 16 ans = ans / n * (n - 1); 17 cout << ans << endl; 18 return 0; 19 }
筛法求欧拉函数:
φ(n)=n*(1-1/p1)(1-1/p2)....(1-1/pk),其中p1、p2…pk为n的所有素因子。
比如:φ(12)=12*(1-1/2)(1-1/3)=4。
利用这个就比较好求了,可以用类似求素数的筛法。
先筛出N以内的所有素数,再以素数筛每个数的φ值。
比如求10以内所有数的φ值:
设一数组phi[11],赋初值phi[1]=1,phi[2]=2...phi[10]=10;
然后从2开始循环,把2的倍数的φ值*(1-1/2),则phi[2]=2*1/2=1,phi[4]=4*1/2=2,phi[6]=6*1/2=3....;
再是3,3的倍数的φ值*(1-1/3),则phi[3]=3*2/3=2,phi[6]=3*2/3=2,phi[9]=.....;
再5,再7...因为对每个素数都进行如此操作,因此任何一个n都得到了φ(n)=n*(1-1/p1)(1-1/p2)....(1-1/pk)的运算
觉得这个“筛”还是比较好用的,也好理解!

1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 5 typedef long long ll; 6 typedef unsigned long long ull; 7 8 #define MAX 10 9 ll phi[MAX]; 10 11 int main() { 12 phi[1] = 1; 13 for (int i = 2; i < MAX; i++) { 14 phi[i] = i; 15 } 16 for (int i = 2; i < MAX; i++) { 17 if (phi[i] == i) { //说明此时的i是素数 18 for (int j = i; j < MAX; j += i) { 19 phi[j] = phi[j] / i * (i - 1); //每个素数倍数的欧拉值乘(1-1/i) 20 } 21 } 22 } 23 for (int i = 1; i < MAX; i++) 24 cout << "phi[" << i << "]=" << phi[i] << endl; 25 return 0; 26 }
