因为武汉的肺炎,导致医院的重要性剧增.虽然已经过了维保也没用续约.但是商务关系还在这里.公司还是安排我们从1号开始继续给之前的合作医院做每天的巡检.
2020年2月7日,检查数据库messages日志.由于之前实施的同志做了切割.服务器一直有日志被切割的提醒.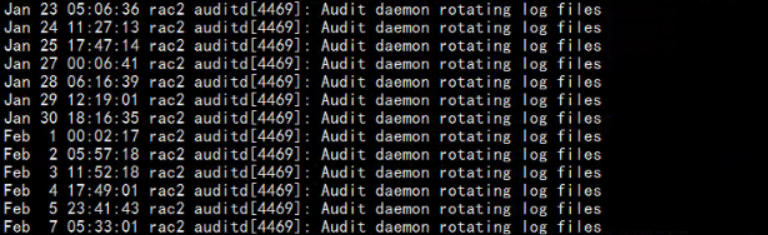
由于当时对日志被切割机制不了解.一直认为被切割后的message-20201119文件为正常的.

所以巡检中仅仅查看了message文件与message-20201119文件.
直到今天2月7号.想对日志切割的机制做下了解.搜索后检查配置文件,发现日志切割的周期为7天,切割的结果是创建一个以切割当天日期为结尾的新文件

至此才发现从19号开始,所有的日志全部丢失了.
通过logrotate -d -v /etc/logrotate.conf 调试.
运行的结果是正常创建messages-20200202的日志文件和删除messages-20201119文件.
但是去掉-d 关闭debug模式执行logrotate,依然没用创建新的日志文件,
怀疑是否是磁盘问题导致写入或者删除失败.于是df -h
结果就hang住了.
我滴天,啥情况.磁盘挂了么.
也不对啊,19号到现在业务都是正常的,如果磁盘挂了,不应该不停业务啊.
打电话给之前实施的同事儿,同事儿说当时存储不够,额外挂了一块nfs磁盘做rman备份用.
检查/etc/fstab 确实有,nfs磁盘/back 目录无法访问.
但是showmount -e 10.20.10.17
能够显示nfs服务器提供的目录.
手动仅仅mount -t nfs 10.20.10.17/back /back成功.
但是使用原先/etc/fstab里面的rw,bg,wsize,rsize,timeo等参数挂载失败.
然后想起检查crontab -l里面执行的备份计划.是rman备份.
ps aux| grep rman |wc -l 结果显示65个备份的进程hang住.
挨个kill掉rman的进程
突然感到后怕.1月22到现在2月7号10多天,rman一直是失败的.是不是归档文件一直没有删除.到时候占满空间数据库会拒绝服务.
赶紧进入sql里面
select * from v$flash_recovery_area_usage
100g空间已经使用了76G.再过一周就会爆掉.
这个时间点,医院停业务估计会被狠狠的屌一顿.真的后怕
回头想想,自己有以下问题.
1) 22号医院重启了rac2服务器,导致日志文件里面产生了大量的信息.所以第一天巡检的时候,我忽略是22号的所有日志.包括当天最后一条nfs故障的告警