梯度下降法与牛顿下降法速度的比较

“牛顿下降法和梯度下降法在机器学习和自适应滤波中都很重要，本质上是为了寻找极值点的位置。但是收敛的速度不同。适当的学习速度，有利于机器学习模型的快速收敛。而过大或者过小的学习速度，都不合适。 下图比较了较小与过大学习速度示意图比较。

较小的学习速度示意图。

• 过大的学习速度示意图。
  

梯度下降算法中，最合适即每次跟着参数θ变化的时候，J(θ)的值都应该下降 到目前为止，我们还没有介绍如何选择学历速率α，梯度下降算法每次迭代，都会受到学习速率α的影响

1. 如果α较小，则达到收敛所需要迭代的次数就会非常高；
2. 如果α较大，则每次迭代可能不会减小代价函数的结果，甚至会超过局部最小值导致无法收敛。如下图所示情况

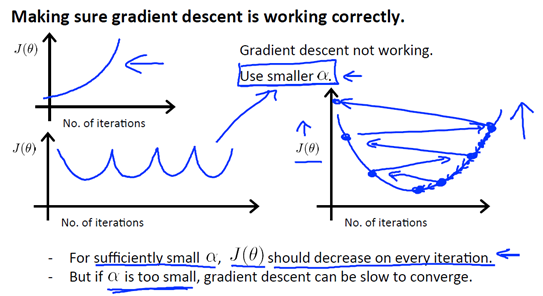
观察下图，可以发现这2种情况下代价函数 J(θ)的迭代都不是正确的

1. 第一个图，曲线在上升，明显J(θ)的值变得越来越大，说明应该选择较小的α
2. 第二个图，J(θ)的曲线，先下降，然后上升，接着又下降，然后又上升，如此往复。通常解决这个问题，还是选取较小的α

根据经验，可以从以下几个数值开始试验α的值，0.001 ,0.003, 0.01, 0.03, 0.1, 0.3, 1, …

α初始值位0.001, 不符合预期乘以3倍用0.003代替，不符合预期再用0.01替代，如此循环直至找到最合适的α

然后对于这些不同的 α 值，绘制 J(θ)随迭代步数变化的曲线，然后选择看上去使得 J(θ)快速下降的一个 α 值。

所以，在为梯度下降算法选择合适的学习速率 α 时，可以大致按3的倍数再按10的倍数来选取一系列α值，直到我们找到一个值它不能再小了，同时找到另一个值，它不能再大了。其中最大的那个 α 值，或者一个比最大值略小一些的α 值 就是我们期望的最终α 值。

感谢博客   http://blog.csdn.net/chenguolinblog/article/details/52138510

 

本文中就牛顿下降法和梯度下降法，哪种收敛方法速度快进行探究“

---

牛顿下降法的递推公式：

xn+1=xn−f′(xn)/f′′(xn)

梯度下降算法的递推公式：

xn+1=xn−μ∗f′(xn)

 

解释一

下图是两种方法的图示表示，红色为牛顿下降法，绿色为梯度下降法，从图中直观的感觉是，红色线短，下降速度快。因为牛顿下降法是用二次曲面去拟合当前的局部曲面，而梯度下降法是用平面去拟合当前的局部曲面，一般用二次曲面拟合的更好，所以一般牛顿算法收敛快。

关于以上的说法中，梯度下降法是用平面去拟合当前的局部曲面。梯度 f’(x)的方向是函数变大的方向。这里需要解释一下，对于一维情况而言，梯度方向只有正方向和负方向。至于为什么梯度下降算法就是用平面去拟合了，大多数情况下，没有讲的详细。接下来就聊一下为什么。

首先考虑一下这个公式，这是一阶泰勒展式，其实就是用平面去拟合函数的局部曲面。

f(x+Δx)=f(x)+f′(x)∗Δx

我们的目的是使得左边的值变小，那是不是应该使得下面的式子变为负值。

f′(x)∗Δx

这样不就会使得左边的式子变小吗。
但是如何使得上式一定为负值，简单的方法就是：

Δx=−f′(x)

这样上式就变为

f(x+Δx)=f(x)−f′(x)∗f′(x)

现在满足使得下式变小了

f(x+Δx)

---

但是不要忘了以上所有的一切只有在局部成立，也就是说在小范围才成立，那么下式就有很能太大

Δx=−f′(x)

所以加个小的修正的因子，上式就变为：

Δx=−μ∗f′(x)

最终得到公式：

xn+1=xn−μ∗f′(xn)

这就是为什么说梯度下降算法是用平面拟合函数的局部曲面。

---

---

至于说牛顿下降法是用二次曲面去拟合当前的局部曲面，首先考虑一下下式：

f(x+Δx)=f(x)+f′(x)Δx+1/2∗f′′(x)∗Δx2

同样我们希望左式最小，那么将左式看成是△x的函数，当取合适的△x值时，左边的式子达到极小值，此时导数为0。因此对上式进行求导数，得到一下公式：

0=f′(x)+f′′(x)∗Δx

此时可得到公式：

xn+1=xn−f′(xn)/f′′(xn)

所以说牛顿下降法是用二次曲面来拟合函数的局部曲面。

---

综上而言，牛顿下降法利用了函数的更多的信息，能够更好的拟合局部曲面，所以收敛的速度也会加快。

解释二

关于梯度下降算法，其中最重要的就是要确定步长μ，它的值严重的影响了梯度下降算法的表现。

接下来考虑如下公式：

f′(x+Δx)=f′(x)+f′′(x)∗Δx

和

Δx=−μ∗f′(x)

结合两个式子，得到：

f′(x+Δx)=f′(x)−μ∗f′′(x)∗f′(x)

令左边的式子为0，得到：

μ=1/f′′(x)

由此可见牛顿下降法是梯度下降法的最优情况，因此牛顿下降法的收敛的速度必然更快。

本文转自以下博客内容，在此表示感谢

http://blog.csdn.net/njucp/article/details/50488869