2021牛客暑期多校训练营9 Cells

题意：有n个人，第i个人站在第((0,a_i))，要走到((0,i))，每次只能往右或者往下走，问所有人路径不相交的方案数

学习了LGV引理，类似容斥的思想，这样的问题转化为求一个行列式

该行列式第i行第j列的元素表示，没有限制，从i走到j的方案数，本题即为( m C_{a_i+j}^j)

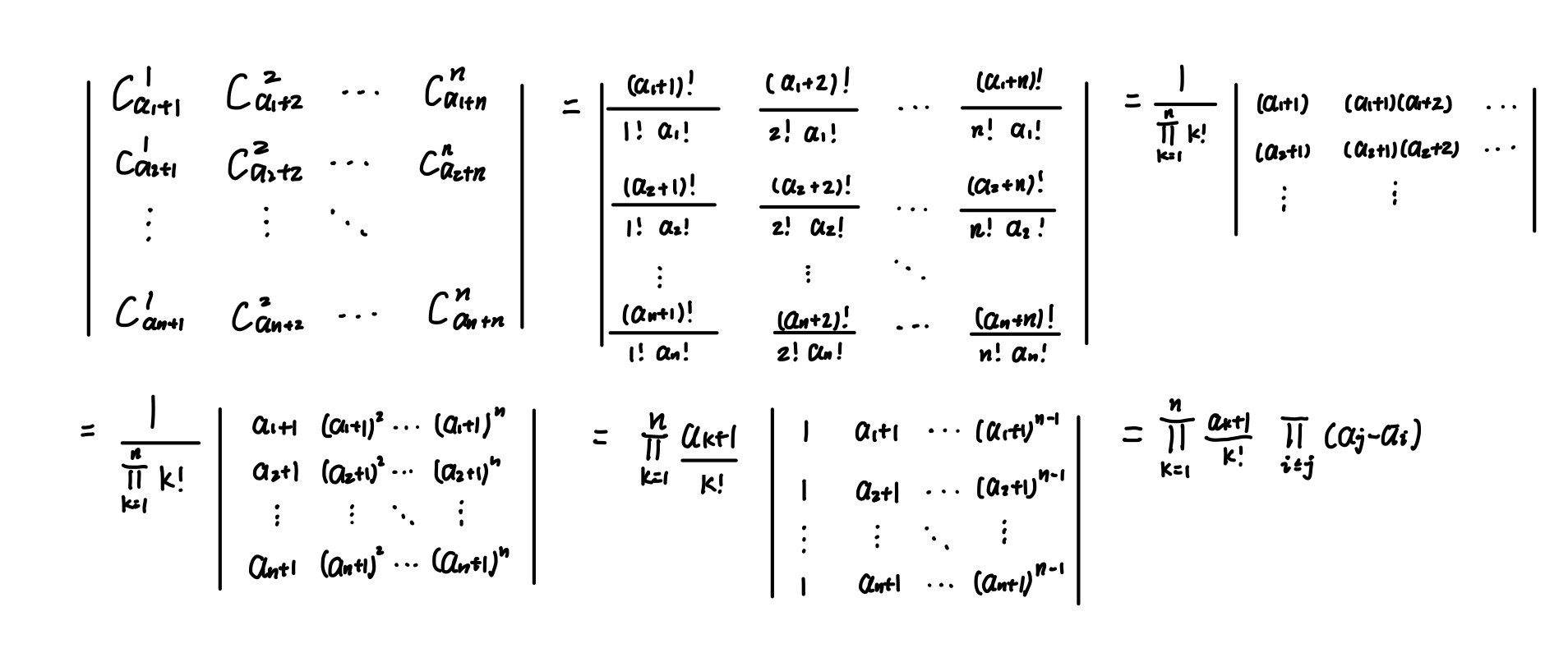
做线代的化简，得到一个范德蒙德行列式，最终要计算的是(prodlimits_{k=1}^ndfrac{a_k+1}{k!}prodlimits_{1le i < jle n}(a_j-a_i))

后面这个东西套路地化为(prod x^{cnt[x]})，即枚举((a_j-a_i))的值，算它出现了几次

这就是{a[i]}和{-a[i]}值域上卷积的形式，加一个偏移量1e6，即可用NTT算出

#include <bits/stdc++.h>
#define int long long
using namespace std;

int rd() {
	int ret = 0, f = 1;
	char c;
	while (c = getchar(), !isdigit(c))
		f = c == '-' ? -1 : 1;
	while (isdigit(c))
		ret = ret * 10 + c - '0', c = getchar();
	return ret * f;
}

typedef long long ll;
typedef unsigned long long ull;

const int MAXN = 5000005;
const int MOD = 998244353, _G = 3;

int limit, r[MAXN << 2];

ll qpow(ll a, ll b = MOD - 2) {
	if(a%MOD==0&&b==0) return 1;
	ll ans = 1;
	while (b) {
		if (b & 1) {
			ans = ans * a % MOD;
		}
		a = a * a % MOD;
		b >>= 1;
	}
	return ans;
}
int bec;
const int invG = qpow(_G);

void NTT(int *g, bool op) {
	int n = limit;
	static unsigned long long f[MAXN << 1], w[MAXN << 1];
	for (int i = 0; i < n; i++)
		w[i] = 1;
	for (int i = 0; i < n; i++)
		f[i] = g[r[i]];

	for (int l = 1; l < n; l <<= 1) {
		ull tG = qpow(op ? _G : invG, (MOD - 1) / (l + l));
		for (int i = 1; i < l; i++)
			w[i] = w[i - 1] * tG % MOD;
		for (int k = 0; k < n; k += l + l) {
			for (int p = 0; p < l; p++) {
				int tt = w[p] * f[k | l | p] % MOD;
				f[k | l | p] = f[k | p] + MOD - tt;
				f[k | p] += tt;
			}
		}

		if (l == (1 << 17))
			for (int i = 0; i < n; i++)
				f[i] %= MOD;
	}
	if (!op) {
		ull invn = qpow(n);
		for (int i = 0; i < n; i++)
			g[i] = f[i] % MOD * invn % MOD;
	} else {
		for (int i = 0; i < n; i++)
			g[i] = f[i] % MOD;
	}
}

void init(int n) {
	limit = 1;
	while (limit <= n)
		limit <<= 1;
	for (int i = 1; i < limit; i++)
		r[i] = r[i >> 1] >> 1 | ((i & 1) ? limit >> 1 : 0);
}


int MTT(int *a, int *b, int n, int m, int *res) {
	static int tmpa[MAXN], tmpb[MAXN];
	for (int i = 0; i < n; i++)
		tmpa[i] = a[i];
	for (int i = 0; i < m; i++)//less
		tmpb[i] = b[i];
	init(n + m);
	NTT(tmpa, 1);
	NTT(tmpb, 1);
	for (int i = 0; i < limit; i++)
		res[i] = 1ll * tmpa[i] * tmpb[i] % MOD;
	NTT(res, 0);

	return n + m - 1;
}

int B[MAXN * 4], tot;

struct P {
	int *a, len, len2;
	void init(int _len, int* src) {
		len = _len;
		a = B + tot;
		for (int i = 0; i < _len; i++)
			a[i]=src[i];
		tot += len;
	}
	void init0(int _len) {
		len = _len;
		a = B + tot;
		tot += len;
	}
};

P mul(const P &lhs, const P &rhs) {
	P ret;
	ret.init0(lhs.len + rhs.len - 1);
	MTT(lhs.a, rhs.a, lhs.len, rhs.len, ret.a);
	return ret;
}

int n;
int a[MAXN];

int fac[MAXN],inv[MAXN];
int AA[MAXN],BB[MAXN];
const int OFFSET = 1e6;

void work() {
	cin >> n;
	fac[0]=1;
	for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
	inv[n]=qpow(fac[n]);
	for(int i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%MOD;
	for(int i=1;i<=n;i++) cin>>a[i];
	int ans=1;
	for(int i=1;i<=n;i++){
		ans=(ans*(a[i]+1)%MOD*inv[i]%MOD);	
	}
	for(int i=1;i<=n;i++){
		AA[OFFSET+a[i]]=BB[OFFSET-a[i]]=1;
	}
	P x,y;
	x.init(OFFSET*2,AA);
	y.init(OFFSET*2,BB);
	P ret=mul(x,y);
	
	for(int i=0;i<OFFSET*2;i++){
		if(ret.a[i]==0) continue;
		ans=(ans*qpow((2*OFFSET-i),ret.a[i])%MOD);	
	}
	if(ans<0) ans+=MOD;
	cout<<ans;
}

signed main() {
	work();
}