2019中山大学程序设计竞赛（重现赛）斐波那契/

2019中山大学程序设计竞赛（重现赛）

1002 三角形（斐波那契）

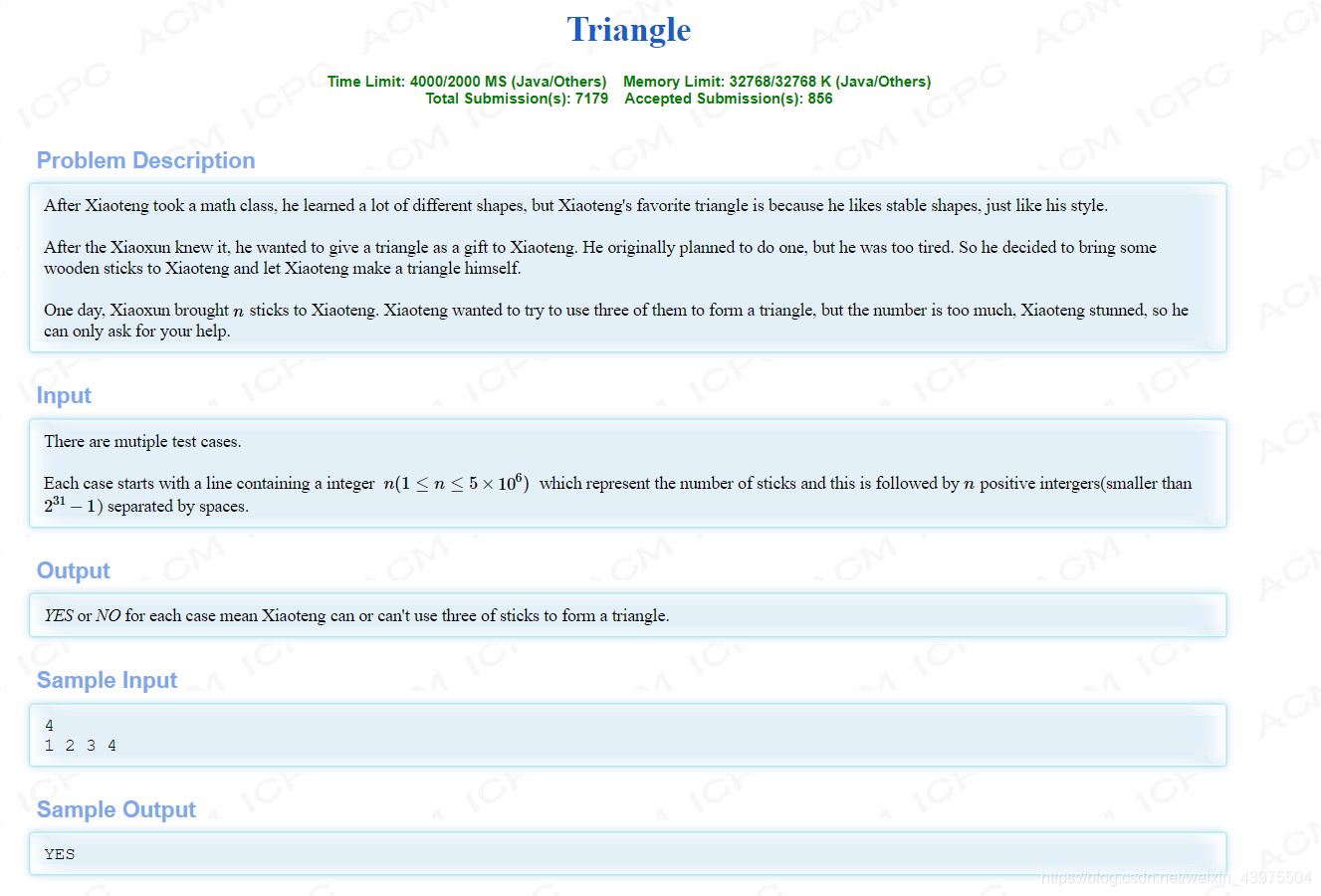
题意：给你n个木棒，判断其能否组成三角形。
这道题当时没做出来，后来看了题解，感觉acm的水还是很深的。

思路：判断能否组成三角形的情况比较多，故判断不能组成三角形的，那就是a[i]+a[i+1]=a[i+2],仔细一看这不是斐波那契数列吗？
因为这个数据量很大5*e6，而且众所周知，斐波那契数列上升速度(指数)还是十分快的。
F(100)=35422484179261915075>2的68次方，远远大于最长的棍子长度。
所以我们可以得出当n>100(50也行)时必能组成三角形。
1.n<100 先排序再进行比较,判断 ai+ai+1>ai+2;
2.n>=100,直接判断"YES";

代码待补完：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<string>
#include<bitset>
#include<utility>
#include<functional>
#include<iomanip>
#include<sstream>
#include<ctime>
#define ll long long
using namespace std;

int k[5000005];

int main()
{
	//ios::sync_with_stdio(false);
	int n;
	while (scanf("%d", &n) != EOF)
	{
		if (n < 50)
		{
			for (int i = 0; i < n; i++)
				scanf("%d", &k[i]);
			sort(k, k + n);
			int flag = 0;
			for (int i = 0; i < n - 2; i++)
			{
				if (k[i] + k[i + 1] > k[i + 2])
				{
					flag = 1;
					break;
				}
			}
			if (flag)
				printf("YES
");
			else printf("NO
");
		}
		else
			cout << "YES" << endl;
	}
	return 0;
}