最近一段时间,看完了项亮大佬的《推荐系统实践》,然后开始看和实践王喆老师的新书《深度学习推荐系统》,整篇博客对自己的代码整理和知识点的回顾。在初次接触后,我对推荐系统的初印象是并不仅仅是算法的学习,还有架构和其他数据处理的知识需要掌握。
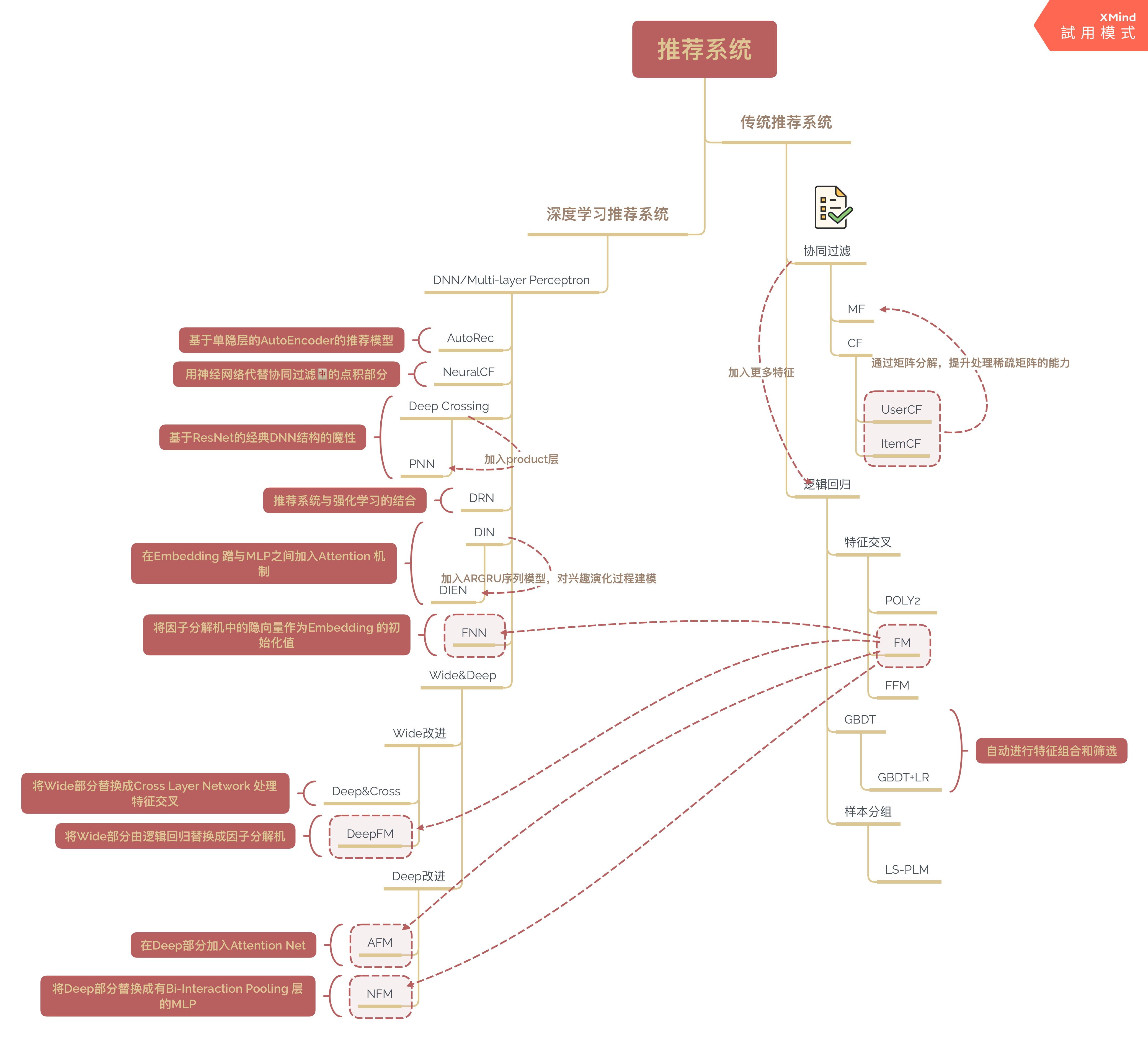
推荐系统前沿 之 协同过滤
初次接触推荐系统,看到最多的字眼便是协同过滤,这也是最基本的推荐系统模型,重在理解推荐系统的基本概念。
《深度学习推荐系统》中对协同过滤的定义是:协同大家的反馈、评价和意见一起对海量信息进行过滤,从中筛选出目标用户可能感兴趣的信息的推荐过程。我对此的理解是一个用户或者物品的属性来源于所有的用户和物品,集体的信息,利用集体的智慧编程找出最合适的结果(灵感来源于《集体智慧编程》)。
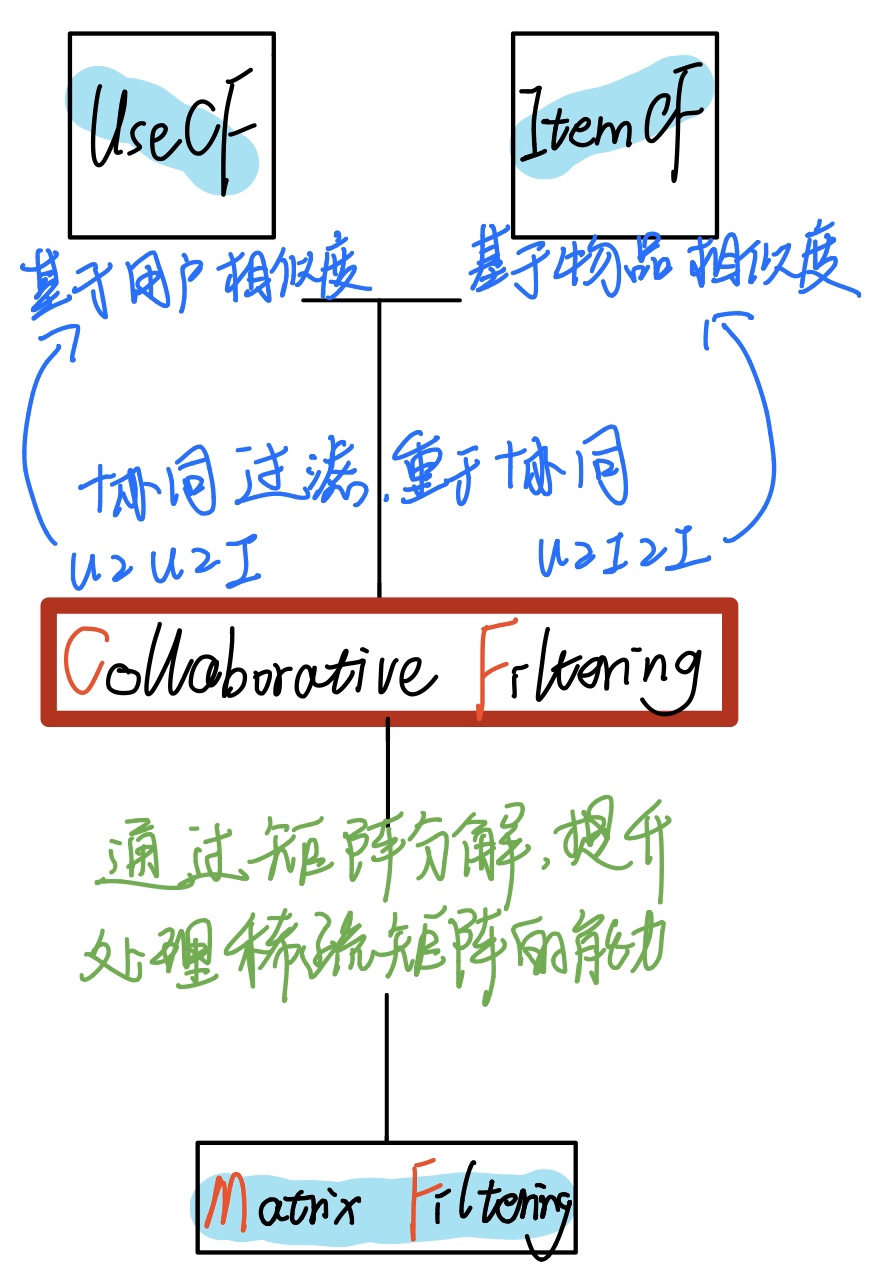
协同过滤主要包括基于用户相似度的推荐(UserCF)和基于物品相似度推荐(ItemCF)。因为在生活实际中,一个用户一般来说只与少部分物品和少部分用户有关联,所以共现矩阵是稀疏的。利用矩阵分解可以加强处理稀疏矩阵的能力。
基本概念
| 名称 | 介绍 |
|---|---|
| 共现矩阵 | 所有用户和所有物品之间关系的矩阵。 |
| 相似度矩阵 | 利用共现矩阵中的用户向量和物品向量以及余弦相似度,皮尔逊相关系数公式求出两两之间的相似度,准确地说是方阵。 |
下图为共现矩阵,行向量为用户向量,列向量为物品向量。
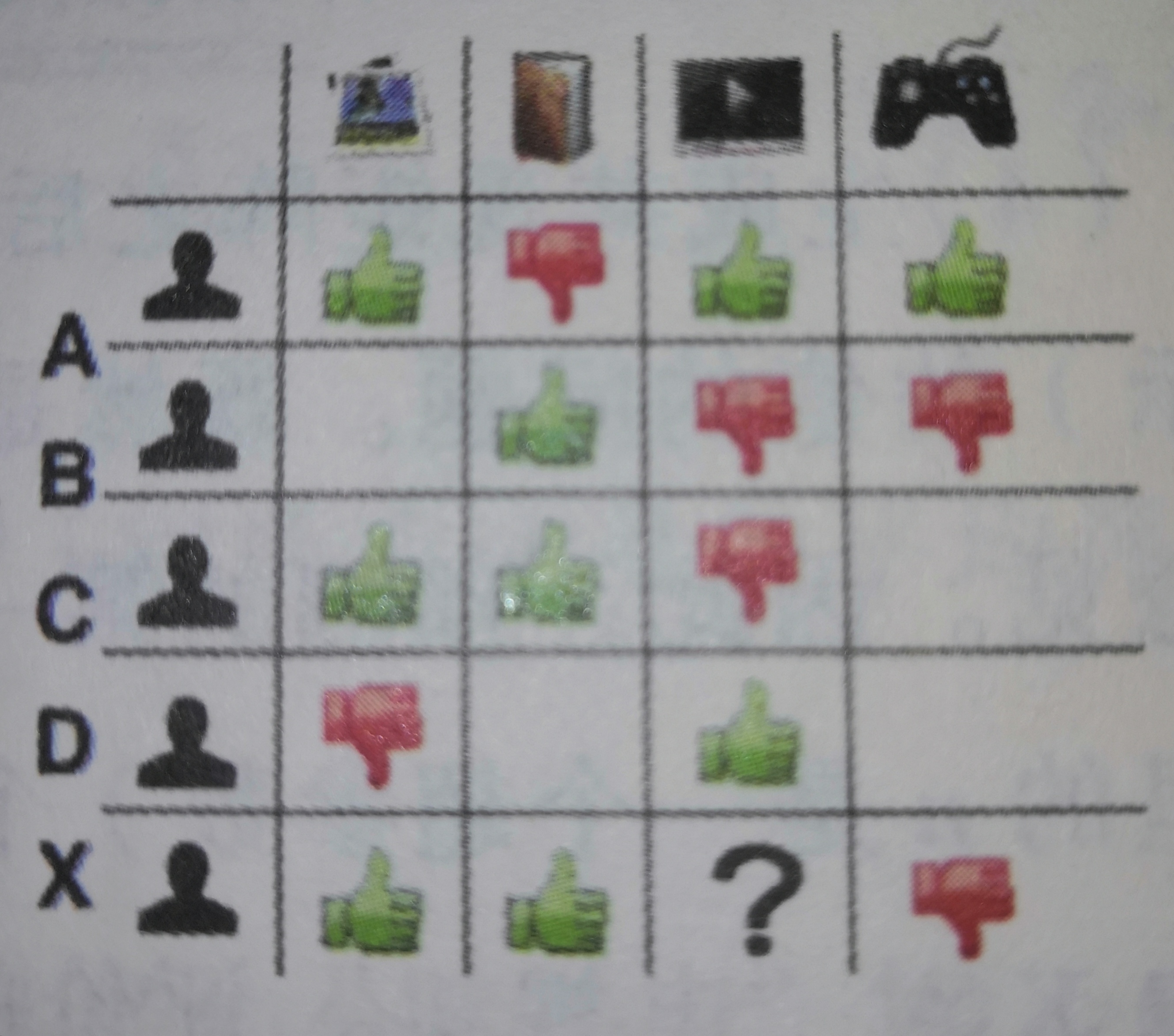
UserCF & ItemCF
协同过滤步骤总体上分为两步,一是计算用户(物品)相似度矩阵,二是利用相似度矩阵给用户推荐物品。
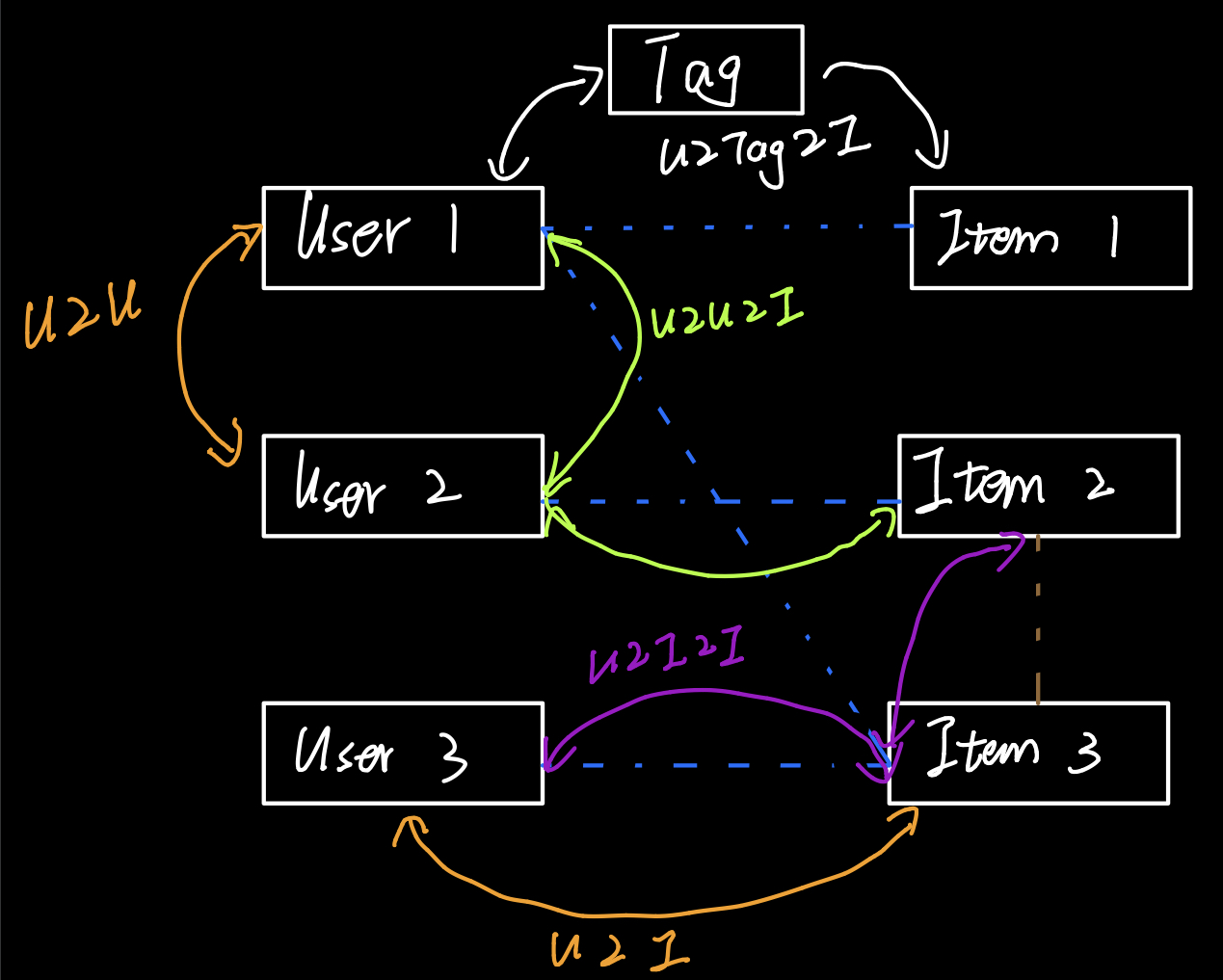
上面图片中对于协同过滤的介绍来自于蚂蚁学python
原理其实就是这么多,主要是实现上的细节问题。我利用Movielens中的100k的数据集进行了验证,代码是能跑通的。利用代码和添加注释来回顾我的实现过程。
| 最后推荐的公式 | 详细 | 参数 |
|---|---|---|
| UserCF | (R_{u,p}=frac{sum_{sin S}(w_{u,s}cdot R_{x,p})}{sum_{sin S}w_{u,s}}) | (w_{u,s})是用户u对用户s的相似度,(R_{s.p}是用户s对物品p的评分) |
| ItemCF | (R_{u,p}=sum_{hin H}(w_{p,h}cdot R_{u,h})) | (w_{p,h})是物品p与物品h的物品相似度,(R_{u,h}是用户u对物品h的已有评分) |
这里的用户相似度、物品相似度公式是比较简单的,一些为了防止热门物品和充分挖掘数据长尾能力的协同过滤方法就会修改相似度公式。
用户相似度的计算使用的是用户对各种物品的评分或者购买情况而不是用户明显的兴趣向量,同理物品相似度使用的是各种用户的对该物品的购买情况而不是物品的内容向量。由此可见是协同过滤,使用的是交互信息。
import pandas as pd
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
import fire
import ipdb
# 没有任何歧义时,u表示某一用户,i表示某一电影,v表示除u以外的另一用户
def Get_data(file,need_cols=['user_id','item_id'],ratings=False):
'''
读取相应的文件
@params
file: 需要打开的文件
need_cols: 需要的列名称,不考虑上下文信息,默认只需要用户和电影名
@return
train:用于训练的共现矩阵
test:用于验证的共现矩阵
'''
print('成功打开{}号文件'.format(file))
train_file,test_file='./ml-100k/u{}.base'.format(file),'./ml-100k/u{}.test'.format(file)
train,test=pd.read_csv(train_file,delimiter=' ',header=None),pd.read_csv(test_file,delimiter=' ',header=None)
train.columns=['user_id','item_id','ratings','timestap']
test.columns=['user_id','item_id','ratings','timestap']
if ratings:
train=pd.crosstab(train['user_id'],train['item_id'],values=train['ratings'],aggfunc=sum)
else:
train=pd.crosstab(train['user_id'],train['item_id']) # 交叉表表示u是否看过了i
test=pd.crosstab(test['user_id'],test['item_id'])
return train,test
def Precision_and_Recall(pred_dict,test):
'''
计算预测率和召回率
@parmas
pred_dict:为用户推荐的电影
test:用于测试的共现矩阵
@return
pre:准确率
rec:召回率
'''
all_pre=0
all_rec=sum(test==1) # 所有应该被预测出来的数,即用户真实看了的电影数
shot=0
for user in pred_dict.keys():
if user not in list(test.index):
continue
for info in pred_dict[user]:
all_pre+=1
if info not in list(test.columns):
continue
if test.loc[user,info]==1:
shot+=1 # 程序运行到这里,表示推荐的电影i,u是将会看的,即推荐成功
return 1.0*shot/all_pre,1.0*shot/all_rec
def Cal_similarty(matrix,categorical='user',method='cosine'):
'''
计算相似度矩阵
@params
matrix:用于训练的共现矩阵
categorical:计算用户相似度矩阵还是物品相似度矩阵,即UseCF还是ItemCF
method:计算相似度的方法,cosine表示利用余弦相似度方法计算相似度
@return
sim_matrix:相似度方阵
'''
print('开始计算相似度矩阵...',end="")
sim_matrix=None
if categorical=='user':
if method=='cosine':
sim_matrix=pd.DataFrame(np.zeros((matrix.shape[0],matrix.shape[0])),index=list(matrix.index),columns=list(matrix.index)) # 初始化用户相似度矩阵
for u in tqdm(list(matrix.index)):
for v in list(matrix.index):
if u==v: # 保持对角线上的元素为0,因为接下来要选择最相似的几个用户,不能包括自己
continue
vector_u,vector_v=sim_matrix.loc[u,:].values,sim_matrix.loc[v,:].values # 用户u,v的用户向量
sim_matrix.loc[u,v]=1.0*np.dot(vector_u,vector_v)/(np.linalg.norm(vector_u,ord=2)*np.linalg.norm(vector_v,ord=2)) # 余弦相似度公式
else:
if method=='cosine':
sim_matrix=pd.DataFrame(np.zeros((matrix.shape[1],matrix.shape[1])),index=list(matrix.columns),columns=list(matrix.columns))
for u in tqdm(list(matrix.columns)):
for v in list(matrix.columns):
if u==v:
continue
vector_u,vector_v=sim_matrix.loc[:,u].values,sim_matrix.loc[:,v].values
sim_matrix.loc[u,v]=1.0*np.dot(vector_u,vector_v)/(np.linalg.norm(vector_u,ord=2)*np.linalg.norm(vector_v,ord=2))
print('DONE')
return sim_matrix
def Recommend(matrix,sim_matrix,N,k=100):
'''
向用户推荐
@params
matrix:用于训练的共现矩阵
sim_matrix:相似度矩阵,现在为指明是何种相似度矩阵
N:每个用户推荐的个数
k:在推荐钱需要选择k个最相似的用户或者物品
@return
rec_dict:为用户推荐的电影
'''
print('开始推荐内容...',end="")
rec=matrix.copy()
rec.loc[:,:]=0 # 保持最好的表示用户行为的方式,共现矩阵
if matrix.shape[0]==sim_matrix.shape[0]: # 指明为UserCF
m_values=matrix.values
for user in rec.index:
sim_values=sim_matrix.loc[user,:].values.reshape(sim_matrix.shape[0],1) # 用户u的相似度向量
val=sorted(sim_values)[-k]
sim_values[sim_values<val]=0 # 选择k个最相似的用户,其他的用户在推荐物品的时候置为0
rec.loc[user,:]=np.sum(sim_values*m_values,axis=0)/np.sum(sim_values) # 利用用户相似度和相似用户评价的加权平均获得目标用户u对物品i的得分,w_u,s和R_s,p为0的进行了计算也不会影响结果
rec.loc[user,(matrix.loc[user,:]>0).tolist()]=0 # 不推荐user已经看过了的
else: # 指明为ItemCF
sim_values=sim_matrix.values
temp_val=np.sort(sim_values,axis=1)[:,-k]
sim_values[sim_values<temp_val]=0 # 选择相似度矩阵中分别和每个物品最相似的前k个物品
for user in rec.index:
m_values=matrix.loc[user,:].values.reshape(matrix.shape[1],1) # 利用用户对物品的兴趣程度R_u,h和该物品对其他物品的相似度w_p,h的乘积,然后对物品维度进行求和表示用户对其他物品的兴趣程度
rec.loc[user,:]=np.sum(m_values*sim_values,axis=0)
rec.loc[user,(matrix.loc[user,:]>0).tolist()]=0 # 不推荐user已经看过了的
# 排序,取前N个推荐结果
rec_dict={}
for user in matrix.index:
rec_dict[user]=list(rec.loc[user,].sort_values(ascending=False).index)[:N]
print('DONE')
return rec_dict
def User_and_Item_CF(need_cols=['user_id','item_id'],categorcial='user',method='cosine',N=50,k=100):
'''
综合成程序
'''
for i in range(1,6):
train,test=Get_data(i)
sim_matrix=Cal_similarty(train,categorcial,method)
pred_dict=Recommend(train,sim_matrix,N,k)
pre,rec=Precision_and_Recall(pred_dict,test)
pd.DataFrame(pred_dict).to_csv('./CF_Recommend/{}_recommend_res{}.csv'.format(categorcial,i))
print('第{}th折:
准确率:{},召回率:{}'.format(i,pre,rec))
Matrix Fatorization
矩阵分解也是来自于协同过滤,矩阵分解中的矩阵是指共现矩阵,传统的方法有特征值分解,奇异值分解和梯度下降。这里主要是实现了梯度下降方法。
矩阵分解是《深度学习推荐系统》中的说法,而在《推荐系统实践》中LFM(latent fator model,隐语义模型)与其十分相似。模型主要是为了每个用户和每个物品找到自己的隐向量(来源于矩阵分解),用户u与物品i的隐向量內积便是u对i的兴趣程度。同时矩阵分解是全局拟合的过程,隐向量是利用全局信息生成。而不像协同过滤,如果两个用户没有相同的历史行为或者两个物品没有相同的人购买,那么两个用户或者两个物品之间的相似度为0,这是很片面的。举个例子,老王购买了联想鼠标和Macbook,李华购买了惠普鼠标和Ipad,那么老王和李华的相似度为0,但是他们的相似度应该很高才对,在隐向量中就可以发现他们对于同一类(电子产品)的兴趣相似,因为隐向量类似于Embedding,对于这个四件物品来说他们相似度很高。
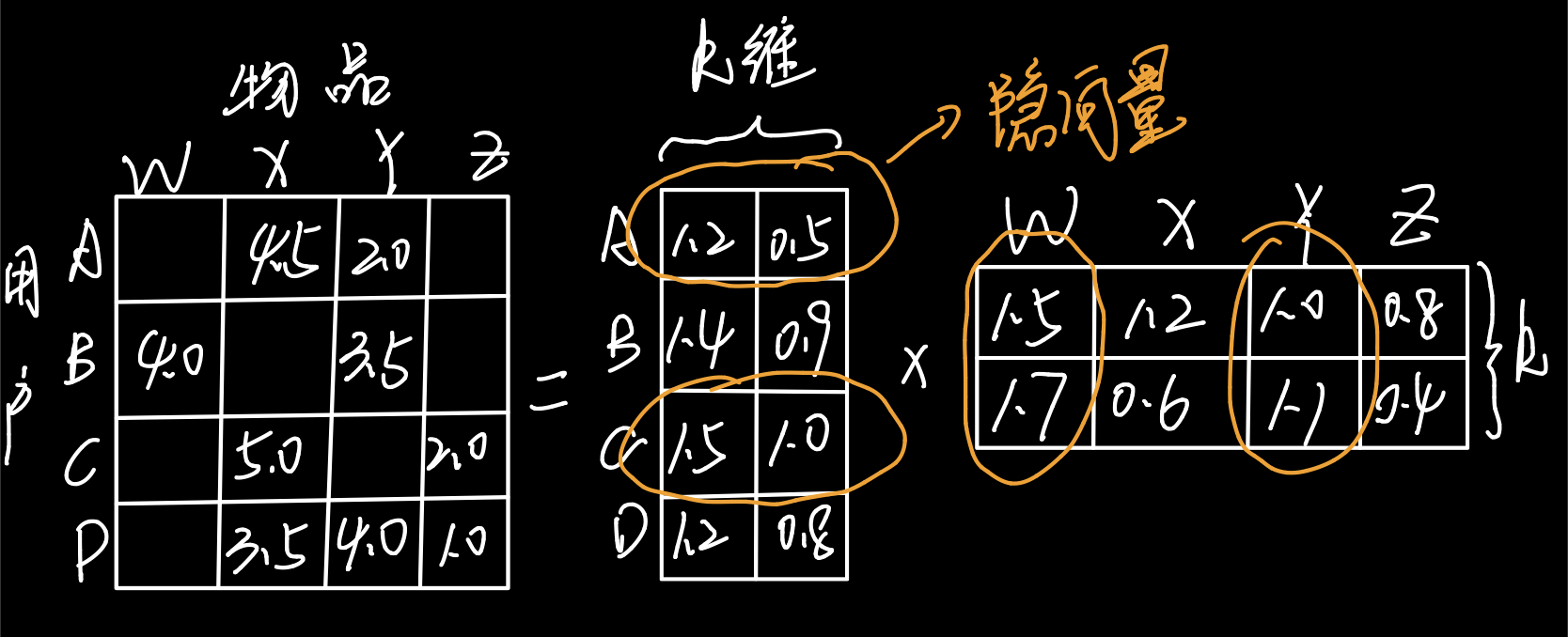
如上图所示。不过还有在隐语义模型中还有一种理解,对于k维(人工决定的)可以视作对所有物品和用户的分成k个维度来描述,用户隐向量是用户分别对k个维度兴趣程度,物品隐向量是物品分别在k个维度的权重,比如对于电影就是科幻,玄幻,爱情等,对于音乐就是电音,轻音乐,R&B等(注意真正学习到的不能保证是这么清楚的分类,有可能是第一类是0.7的电音加上0.3的轻音乐,但是能保证如果两个物品的隐向量相似度大则他们的类型一定相似)
| 参数 | 解释 |
|---|---|
| (hat{r}_{ui}) | 用户u对物品i的(预测)兴趣程度 |
| (q_i) | 物品i的隐向量 |
| (p_u) | 用户u的隐向量 |
| (K) | 用户评分样本集合 |
| (mu) | 全局偏差系数 |
| (b_u) | 用户偏差系数 |
| (b_i) | 物品偏差系数 |
| (lambda) | 正则化系数 |
| (alpha) | 学习速率 |
目标是训练数据集中(r_{ui})和(hat{r}_{ui})的差距最小,即(min sum_ limits{(u,i)in K}(r_{ui}-hat{r}_{ui})^2)
| 公式 | 解释 |
|---|---|
| (min_ limits{q^*,p^*}sum_ limits{(u,i)in K}(r_{ui}-hat{r}_{ui})^2) | 基本的目标公式 |
| (min_ limits{q^*,p^*}sum_ limits{(u,iin K)}(r_{ui}-q_i^Tp_u)^2+lambda(|q_i|+|p_u|)^2) | 基本的目标梯度下降公式 |
| (min_ limits{q^*,p^*,b^*}sum_ limits{(u,iin K)}(r_{ui}-mu-b_u-b_i-q_i^Tp_u)^2+lambda({|q_i|}^2+{|p_u|}^2+b_u^2+b_i^2)) | 加上偏置的目标梯度下降公式 |
| ...梯度公式不怎么好描述... | 我一般靠画图和矩阵维度对称(狗头) |
代码注释
def Initial_Vector(train,latent_dim):
'''
初始化隐向量
@params
train:共现矩阵
latent_dim:隐向量的维度
@return
user_matrix:用户隐向量
item_matrix:物品隐向量
mu:全局偏差系数
bias_user:用户偏差系数
bias_item:物品偏差系数
'''
user_dim,item_dim=train.shape
user_matrix=np.random.randn(user_dim,latent_dim)
item_matrix=np.random.randn(latent_dim,item_dim)
mu=train.mean()
bias_user=np.mean(train,axis=1).reshape((user_dim,1))
bias_item=np.mean(train,axis=0).reshape((1,item_dim))
return user_matrix,item_matrix,mu,bias_user,bias_item
def Cal_loss(train,u_matrix,i_matrix,mu,bias_user,bias_item,lambd):
'''
计算损失
@param
lambd:正则化系数
@return
punish:计算公式造成的损失
regula:正则化造成的损失
'''
pq=train-u_matrix@i_matrix-mu-bias_user-bias_item # 这里将train==0的位置,也就是train集中用户并没有看到的电影无法打分,
pq[train==0]=0 # 在训练集中标识为0,那么在这个计算出来的评分中也要标识为0,避免造成多余的损失
punish=np.sum(np.power(pq,2)) # 注意不能将ratings=0而不做上述操作进行运算(偷换了概念,用户没有看计算出来的损失不能用于梯度下降)
regula=lambd*(np.sum(np.power(bias_user,2))+np.sum(np.power(bias_item,2))+np.sum(np.power(u_matrix,2))+np.sum(np.power(i_matrix,2)))
return punish+regula
def Cal_gradient(train,u_matrix,i_matrix,mu,bias_user,bias_item,lambd):
'''
计算梯度
'''
pq=train-u_matrix@i_matrix-mu-bias_user-bias_item
pq[train==0]=0
bu_num=np.sum((train!=0),axis=1) # 对用户和物品偏差系数进行求梯度时,要注意用户并没有进行评价的信息(空白信息)
bi_num=np.sum((train!=0),axis=0) # 上面两行剔除了空白信息的梯度附加
dera_u=-2*pq@i_matrix.T+2*lambd*u_matrix
dera_i=-2*u_matrix.T@pq+2*lambd*i_matrix
dera_bu=np.sum((-2*pq),axis=1)+2*lambd*np.multiply(bu_num,bias_user.squeeze())
dera_bi=np.sum((-2*pq),axis=0)+2*lambd*np.multiply(bi_num,bias_item.squeeze())
return dera_u,dera_i,dera_bu.reshape((dera_bu.shape[0],1)),dera_bi.reshape((1,dera_bi.shape[0]))
def Re_train(train,latent_dim=5,epoches=50,lr=0.1):
'''
训练,进行梯度下降
@params
epoches:迭代次数
lr:学习速率
@return
res_dict:矩阵分解的参数,用户物品隐向量和各种偏差系数
'''
u_matrix,i_matrix,mu,bu,bi=Initial_Vector(train,latent_dim)
loss=[]
for i in tqdm(range(1,epoches+1)):
loss.append(Cal_loss(train,u_matrix,i_matrix,mu,bu,bi,lr))
dera_u,dera_i,dera_bu,dera_bi=Cal_gradient(train,u_matrix,i_matrix,mu,bu,bi,lr)
u_matrix=u_matrix-lr*dera_u
i_matrix=i_matrix-lr*dera_i
bu=bu-lr*dera_bu
bi=bi-lr*dera_bi
if i%10==0:
print('{}th Epoch Loss is {}'.format(i,loss[-1]))
plt.figure()
plt.plot(np.arange(1,len(loss)+1),loss,'go-')
plt.xlabel('EPOCH')
plt.ylabel("LOSS")
plt.title("Training Loss")
plt.show()
res_dict={'u_matrix':u_matrix,'i_matrix':i_matrix,'bu':bu,'bi':bi,'mu':mu}
return res_dict
def Predict(train_df,res_dict,N=40):
'''
为所有用户推荐物品
@param
train_df:共现矩阵,此时是DataFrame格式
res_dict:矩阵分解的参数
N:每个用户推荐的个数
@return
result:为所有用户推荐的电影
'''
u_matrix,i_matrix,bu,bi,mu=res_dict['u_matrix'],res_dict['i_matrix'],res_dict['bu'],res_dict['bi'],res_dict['mu']
pred=pd.DataFrame((u_matrix@i_matrix+bu+bi+mu),index=train_df.index,columns=train_df.columns)
pred[train_df>0]=0
result=dict()
for user in list(pred.index):
result[user]=list(pred.loc[user,:].sort_values(ascending=False).index)[:N]
return result
def Matrix_seperate(lr=0.0000001,latent_dim=5,epoches=50,N=40):
# ipdb.set_trace()
for i in range(1,6):
print("开始读取数据...",end="")
train_df,test=Get_data(i,ratings=True)
train_df=train_df.fillna(0)
print('DONE')
train=train_df.values
print("开始第{}次训练...".format(i))
res_dict=Re_train(train,latent_dim,epoches,lr)
result=Predict(train_df,res_dict,N)
pd.DataFrame(result).to_csv('./CF_Recommend/Matrix_seperate_{}.csv'.format(i))
pre,rec=Precision_and_Recall(result,test)
print("{}th 交叉验证
准确率:{},召回率:{}".format(i,pre,rec))
总结一下:这个矩阵分解中就是数学上的运算转换成代码有点难度,注意理解和分析(我是在写这篇博客才发现之前的代码错了,如果还是错了,请指正)
数据集
这里将我的数据打包放在百度网盘了,需要自取。密码: gwoa
人生此处,绝对乐观