正态分布

正态分布

正态分布代表了宇宙中大多数情况的运转状态。大量的随机变量被证明是正态分布的。

若随机变量X服从一个数学期望为μ、方差为$sigma ^{2}$的正态分布，记为$N=left( mu ,sigma ^{2} ight) $。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0，σ=1时的正态分布是标准正态分布。

公式$$fleft( x| mu ,sigma ight) =dfrac {1}{sqrt {2pi sigma ^{2}}}e^{-dfrac {left( x-mu ight) ^{2}}{2sigma ^{2}}}$$

μ是均值，σ是标准差。

---

正态分布相关python代码

导入库

#导入库
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

概率密度函数

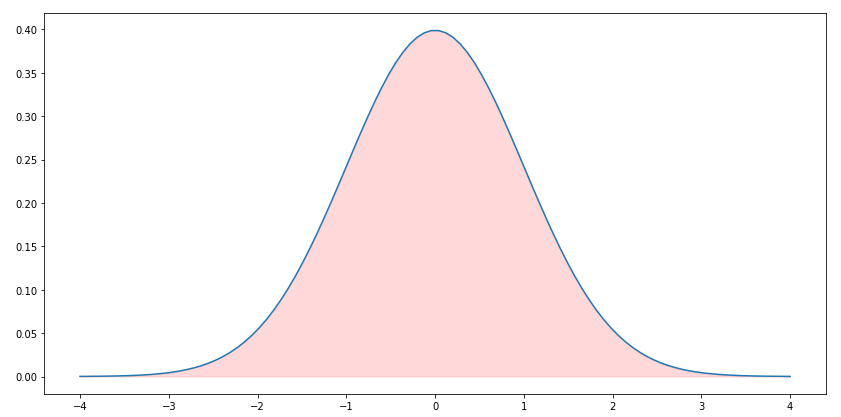
显示一个标准PDF图。

#PDF概率密度函数
plt.figure(figsize=(14,7))

plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100)),
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100)),
                 alpha=0.15,
                 color='red',
                )

plt.show()

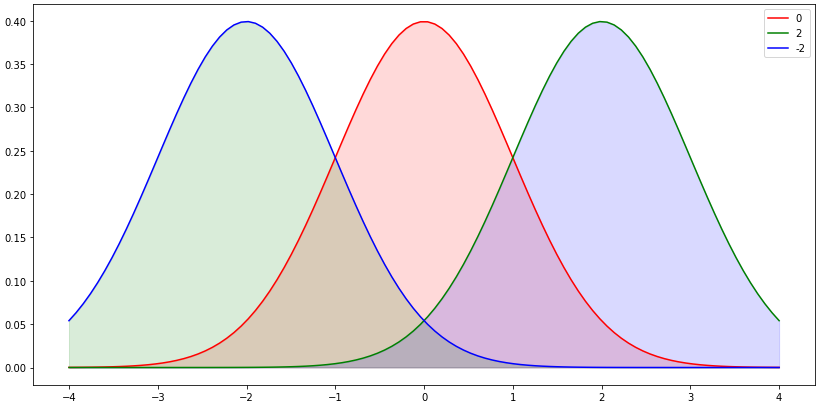
 均值

不同均值影响的是PDF图像的位置。

#均值的影响
plt.figure(figsize=(14,7))

plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100),loc=0),
         color='r',
         label='0'
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100),loc=0),
                 alpha=0.15,
                 color='r',
                )

#均值是2
plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100),loc=2),
         color='g',
         label='2'
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100),loc=2),
                 alpha=0.15,
                 color='b',
                )

#均值是-2
plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100),loc=-2),
         color='b',
         label='-2'
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100),loc=-2),
                 alpha=0.15,
                 color='g',
                )

plt.legend()
plt.show()

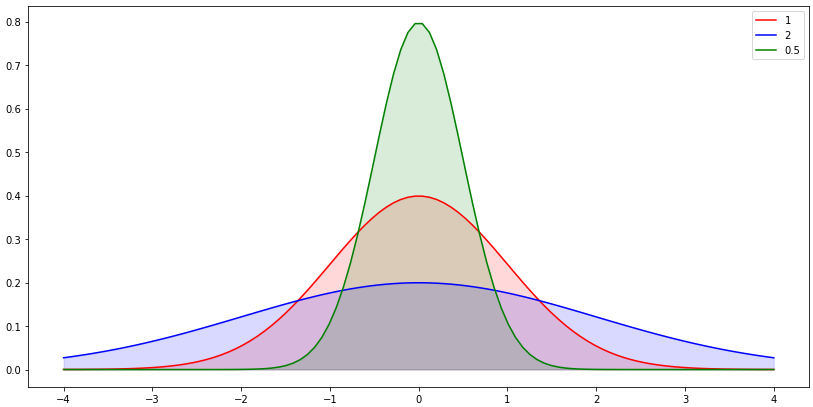
 标准差

标准差影响的是PDF图像的分布幅度。

#标准差的影响
plt.figure(figsize=(14,7))

#标准差是1
plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100),scale=1),
         color='r',
         label='1',
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100),scale=1),
                 alpha=0.15,
                 color='r',
                )

#标准差是2
plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100),scale=2),
         color='b',
         label='2',
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100),scale=2),
                 alpha=0.15,
                 color='b',
                )

#标准差是0.5
plt.plot(np.linspace(-4,4,100),
         stats.norm.pdf(np.linspace(-4,4,100),scale=0.5),
         color='g',
         label='0.5',
        )
plt.fill_between(np.linspace(-4,4,100),
                 stats.norm.pdf(np.linspace(-4,4,100),scale=0.5),
                 alpha=0.15,
                 color='g',
                )

plt.legend()
plt.show()

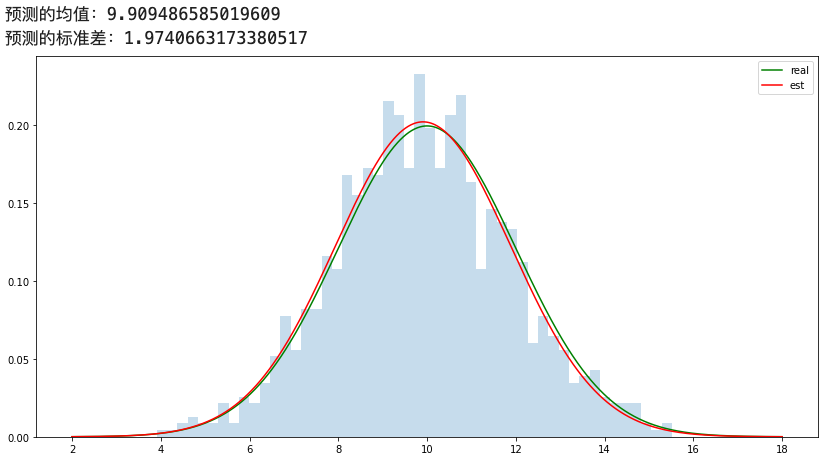
 随机样本分布

#真实的均值和标准差
plt.figure(figsize=(14,7))

mu_real=10
sigma_real=2

#随机样本
np.random.seed(0)
sample=stats.norm.rvs(loc=mu_real,scale=sigma_real,size=1000)

#样本的均值和标准差
mu_est=np.mean(sample)
sigma_est=np.std(sample)
print('预测的均值：{}
预测的标准差：{}'.format(mu_est,sigma_est))

#绘制样本的直方图
plt.hist(sample,bins=50,density=True,alpha=0.25)

#真实的PDF
plt.plot(np.linspace(2,18,1000),stats.norm.pdf(np.linspace(2,18,1000),loc=mu_real,scale=sigma_real),color='g',label='real')

#样本的PDF
plt.plot(np.linspace(2,18,1000),stats.norm.pdf(np.linspace(2,18,1000),loc=mu_est,scale=sigma_est),color='r',label='est')

plt.legend()
plt.show()

 累积概率密度函数

#CDF累积概率密度函数
plt.figure(figsize=(14,7))

plt.plot(np.linspace(-4,4,100),
         stats.norm.cdf(np.linspace(-4,4,100)),
        )

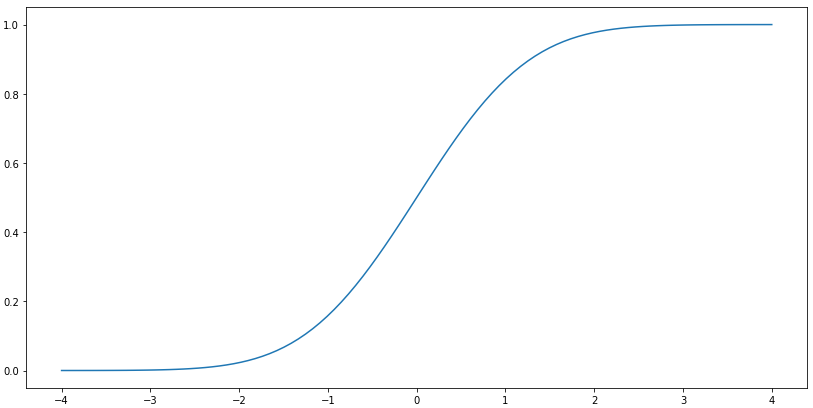
 区间概率

print('P(X<0.3)={}'.format(stats.norm.cdf(0.3)))
print('P(-0.2<X<0.2)={}'.format(stats.norm.cdf(0.2)-stats.norm.cdf(-0.2)))