卡方分布
通过小数量的样本容量去预估计总体容量的分布情况。卡方检验是统计样本的实际观测值与理论推断值之间的偏离程度,基本思想是根据样本数据推断总体的频次与期望频次是否有显著性差异。
如果n个相互独立的随机变量均服从标准正态分布,则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布。
自由度:假设随机取n个样本,但又要求这n个样本均值固定,那么就有一些样本不能随意的取值,剩下可以随意取值的样本个数就是自由度。
卡方分布的概率密度函数为:
当x>0时,$fleft( x|k ight) =dfrac {x^{dfrac {k}{2}-1}e^{-dfrac {x}{2}}}{2^{dfrac {k}{2}}Gamma left( dfrac {k}{2} ight) }$
当$xleq 0$时,$fleft( x|k ight) =0$
k是自由度。
卡方分布相关代码
#导入库 import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats
#PDF plt.figure(figsize=(14,7)) x=np.linspace(0,20,100) y=stats.chi2.pdf(x,df=4) plt.plot(x,y,color='b',label='PDF') plt.fill_between(x,y,color='b',alpha=0.25) plt.legend() plt.show()
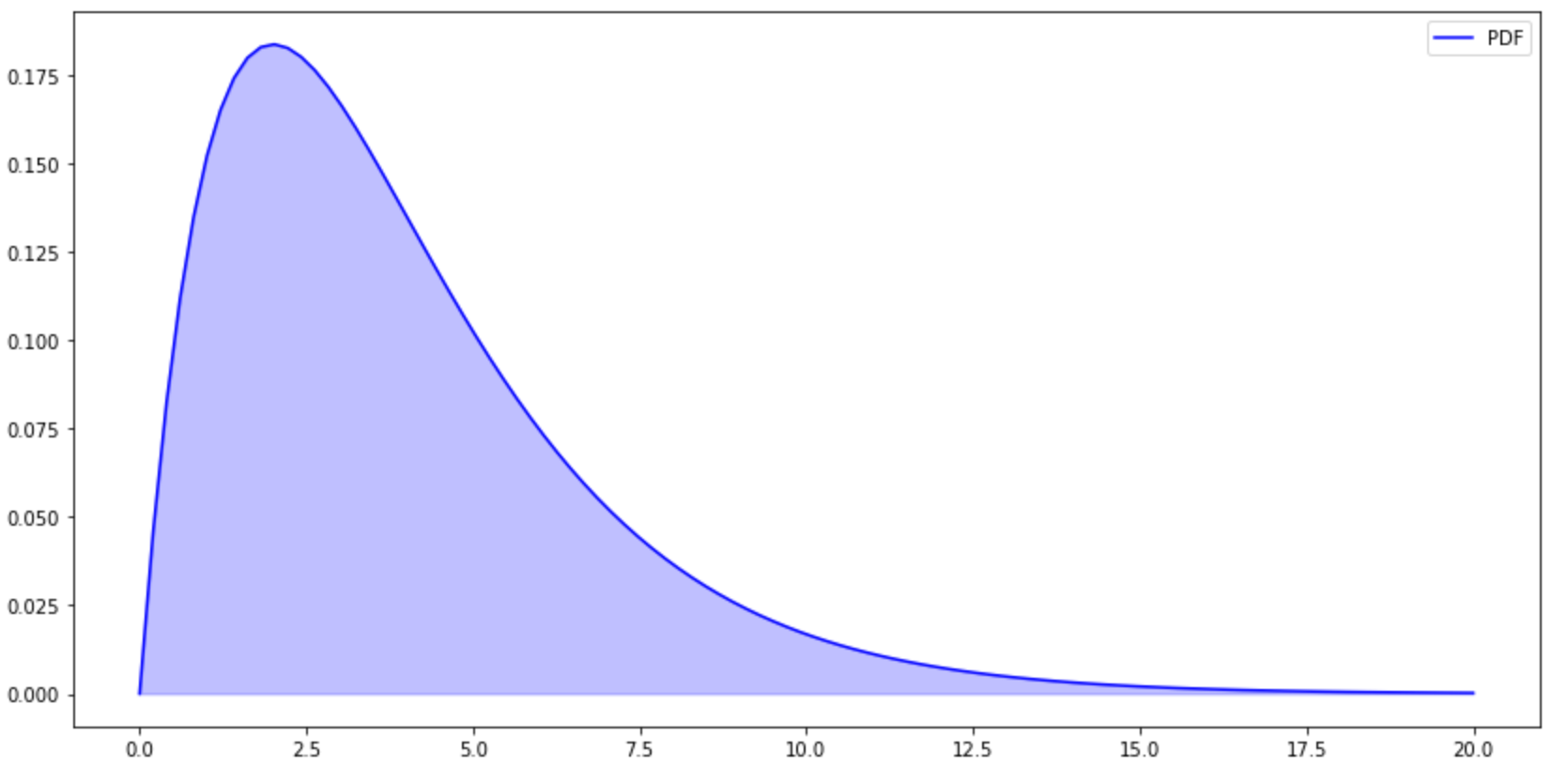
自由度
#自由度的影响 plt.figure(figsize=(14,7)) x=np.linspace(0,20,100) y1=stats.chi2.pdf(x,df=1) y2=stats.chi2.pdf(x,df=3) y3=stats.chi2.pdf(x,df=6) plt.plot(x,y1,color='r',label='k=1') plt.fill_between(x,y1,color='r',alpha=0.25) plt.plot(x,y2,color='g',label='k=3') plt.fill_between(x,y2,color='g',alpha=0.25) plt.plot(x,y3,color='b',label='k=6') plt.fill_between(x,y3,color='b',alpha=0.25) plt.legend() plt.show()
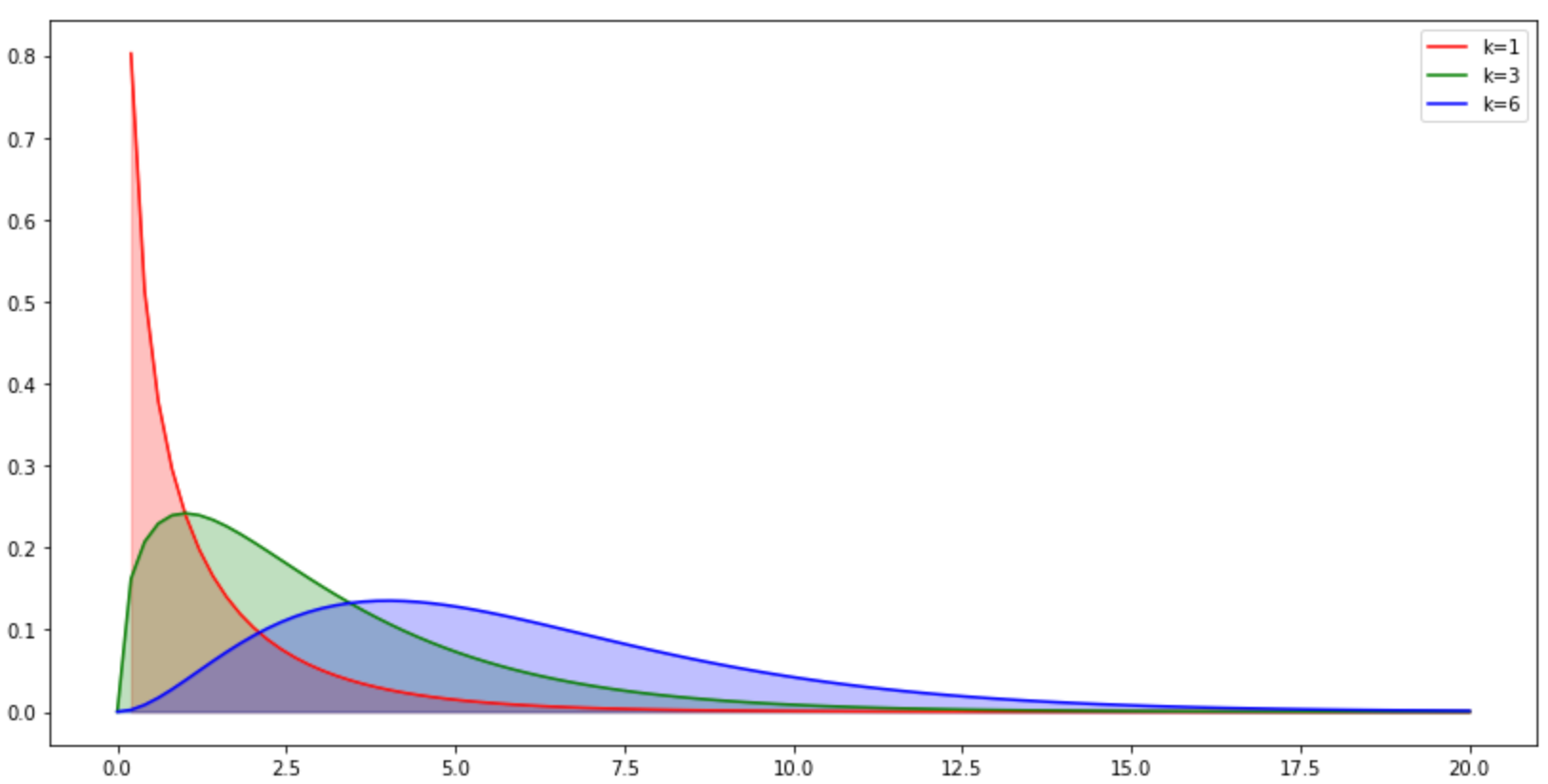
随机样本
np.random.seed(0) print(stats.chi2.rvs(df=4),end=' ') print(stats.chi2.rvs(df=4,size=10),end=' ')
![]()
CDF
#CDF plt.figure(figsize=(14,7)) x=np.linspace(0,20,100) y=stats.chi2.cdf(x,df=4) plt.plot(x,y,color='b',label='CDF') plt.legend() plt.show()
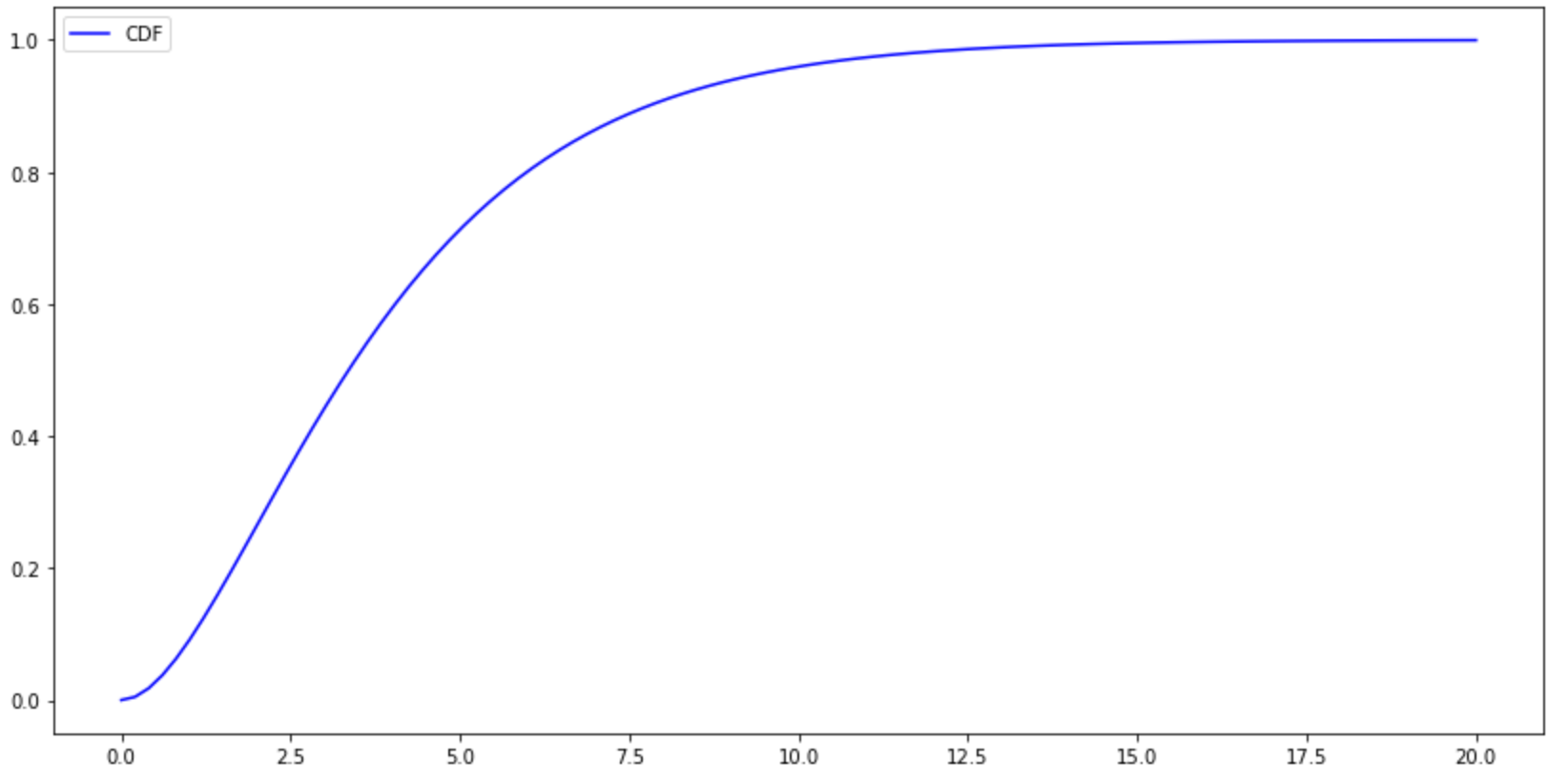
区间概率
print(' P(X<=3)={} '.format(stats.chi2.cdf(x=3,df=4))) print('P(2<X<=8)={} '.format(stats.chi2.cdf(x=8,df=4)-stats.chi2.cdf(x=2,df=4)))
