Delta-wave
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 4684 Accepted Submission(s): 1777
Problem Description
A triangle field is numbered with successive integers in the way shown on the picture below.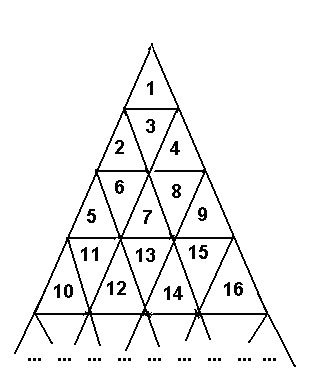 
Write the program to determine the length of the shortest route connecting cells with numbers N and M.
Write the program to determine the length of the shortest route connecting cells with numbers N and M.
Input
Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).
Output
Output should contain the length of the shortest route.
Sample Input
6 12
Sample Output
3
Source
思路：
比如6 16 向右移一格..经过两条边即可...然后将其分层，确定他们的行列来计算相应的值即可。。哎呀，说不清了..来看代码ba!。。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 using namespace std; 7 int sum(int m,int &cc) 8 { 9 10 int rr=(int)sqrt(1.0*m); //确定她所在第几行..一右边为参数 11 if(rr*rr!=m) rr++; 12 cc=rr*rr-m; 13 if(cc&1) 14 return 2*(rr-1); 15 else 16 return 2*rr-1; 17 } 18 19 int main() 20 { 21 int n,m,ncc,mcc,add; 22 while(cin>>m>>n) 23 { 24 int rankn=sum(n,ncc); //得到n的所在第几行 25 int rankm=sum(m,mcc); //得到m的所在第几行 26 ncc>>=1; //得到n所在第几列，以右边为参数 27 mcc>>=1; //得到m所在第几列，以右边为参数 28 //此处可以进一步优化...现在就不优化了.. 29 if(rankn==rankm) 30 cout<<abs(n-m)<<endl; 31 else 32 if(rankn<rankm) 33 { 34 35 if(mcc>=ncc&&mcc<=(rankm-rankn)/2+ncc) 36 cout<<(rankm-rankn)<<endl; 37 else 38 { 39 40 if(2*mcc<(rankm-rankn)/2+2*ncc) 41 { 42 add=ncc-mcc; 43 cout<<2*add+(rankm-rankn)<<endl; 44 } 45 else 46 { 47 add=mcc-((rankm-rankn)/2+ncc); 48 cout<<2*add+(rankm-rankn)<<endl; 49 } 50 51 } 52 } 53 else 54 { 55 //rankn>rankm 56 if(ncc>=mcc&&ncc<=(rankn-rankm)/2+mcc) 57 cout<<(rankn-rankm)<<endl; 58 else 59 { 60 if(2*ncc<(rankn-rankm)/2+2*mcc) 61 { 62 add=mcc-ncc; 63 cout<<2*add+(rankn-rankm)<<endl; 64 } 65 else 66 { 67 add=ncc-((rankn-rankm)/2+mcc); 68 cout<<2*add+rankn-rankm<<endl; 69 } 70 } 71 } 72 /* cout<<0&1<<endl;*/ 73 } 74 75 return 0; 76 }