Dreamoon loves summing up something for no reason. One day he obtains two integers a and b occasionally. He wants to calculate the sum of all nice integers. Positive integer x is called nice if 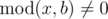 and
and 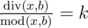 , where k is some integer number in range [1, a].
, where k is some integer number in range [1, a].
By 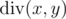 we denote the quotient of integer division of x and y. By
we denote the quotient of integer division of x and y. By 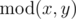 we denote the remainder of integer division of x and y. You can read more about these operations here: http://goo.gl/AcsXhT.
we denote the remainder of integer division of x and y. You can read more about these operations here: http://goo.gl/AcsXhT.
The answer may be large, so please print its remainder modulo 1 000 000 007 (109 + 7). Can you compute it faster than Dreamoon?
The single line of the input contains two integers a, b (1 ≤ a, b ≤ 107).
Print a single integer representing the answer modulo 1 000 000 007 (109 + 7).
1 1
0
2 2
8
For the first sample, there are no nice integers because 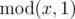 is always zero.
is always zero.
For the second sample, the set of nice integers is {3, 5}.
题意:
给你两个整数a,b ,定义这样一个数为漂亮数:
(1) x>0 ; (2)x%b!=0 ; (3) (x/b)/(x%b)=k; (4)k属于[1,a];
求这样的漂亮数的所有之和。
对于这样题,分析起来其实还是很简单的, 对于求和(sum),我们需要做的第一件事就是确定漂亮数的边界(上限和下限)、由于(3) (x/b)/(x%b)=k
可以得出: x/b = k*(x%b); x%b的剩余系即{1,2,3,4,5,......b-1}里的最大系;我们不放设定y={1,2,3,4,5,........b-1};
不难得出: x=k*y*b+y; -->x=(k*b+1)*y 所以可以推断公式: x=Σ1a (k*b+1)*Σ1b-1 (y);
进一步简化后部分: x=Σ1a (k*b+1)*(b-1)*(b)/2;
所以代码为:

1 #include<cstdio> 2 #include<cstring> 3 #define LL __int64 4 #define mod 1000000007 5 int main() 6 { 7 LL a,b; 8 LL sum; 9 while(scanf("%I64d%I64d",&a,&b)!=EOF) 10 { 11 sum=0; 12 for(LL j=1;j<=a;j++) 13 { 14 sum+=((j*b)%mod+1)%mod; 15 sum%=mod; 16 } 17 LL ans=(((b-1)*b)/2)%mod; 18 printf("%I64d ",(sum*ans)%mod); 19 } 20 return 0; 21 }
