扔鸡蛋

887. 鸡蛋掉落

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

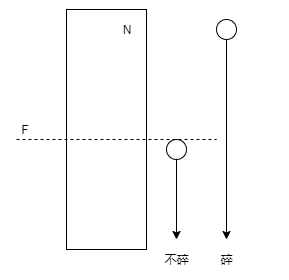
你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

本题是谷歌用于面试的一道经典面试题之一。由于本题过于经典，谷歌公司已经不再将这题作为面试的候选题目了。

思路

假设(N=100)

• 如果只有一个蛋 (K=1)

  只能从第一层开始，一层一层往上试，最差情况就要扔100次

• 无限个蛋 (K=infty)

  使用二分查找

​ 第一个蛋从50楼开始扔，如果碎了，那么临界楼层就在0-50之间，否则就在50-100；

​ 第二个蛋在25层扔，碎了，在0-25之间，否则在25-50

​ 所以要扔的次数(M)满足 $2^M >= 100 , M>=6.64 $, 至少需要7次

• 两个蛋(K=2)

  试想一下，如果第一个蛋在某些情况下碎了，那就只剩下一个蛋，退化为第一种问题，只能一层一层往上试，所以第一个蛋的作用应该在与缩小范围，然后用第二个蛋试

  两个蛋(A,B)

  A：先在第10层扔，没碎就在20层扔，没碎在30层扔……。也就是依次在10,20，……，100层扔，A最多可以扔10次

  B：假如A已经确定了范围，在10层没碎，在20层碎了，那么就用B在10-20依次尝试。

  最坏情况下A在100层碎了，B在99层碎了，需要10+9次

在刚才的情况中，每次扔鸡蛋的楼层都是等间隔的，B每次要扔的次数都是一样的，如果临界楼层比较靠后，A扔的次数就多了，如果让间隔变得不等，A每多扔一次，B的范围就缩小一次，这样总次数就可以平均下，也许会更好，我们尝试下

第一次在第n层扔，第二次加n-1层，第三次加n-2层……，也就是A每次扔的间隔都会缩小一，(n,n-1,n-2,...) ，(1+2+3+……+n=n(n+1)/2>=100 ，n>=13.65)，取n=14

A： 14, 27，39， 50， 60， 69 ，77， 84， 90， 95， 99, 100

这种方法扔鸡蛋次数在12-14之间，最坏情况14次

• (K)个蛋，(N)层，最小移动次数(M(K,N))

先从最简单情况说起，画一个表，3层楼，4个蛋

	1	2	3	4
1	1	1	1	1
2	2
3	3

第一行，只有一层楼

第一列，只有一个蛋

假如第一个蛋在(T)层扔，碎，临界楼层在前面，不碎，在后面

最坏情况下要扔多少层：(max{M(K-1,T-1),M(K,N-T)}+1 = M_T(K,N))

表示在第一个蛋扔到(T)层时，需要扔鸡蛋的个数，不要忘了加1（扔到第(T)层的一次操作）

问题来了，第一个(T)怎么确定？

最直接的方法就是遍历，以每层作为起始的第一个(T)

T	1	2	……	N
(M_T)	(M_1)	(M_2)	……	(M_N)

第一个蛋可以扔在任意一层，在所有扔法中选最小值

(M(K,N) = min{M_1,M_2,……,M_N})

利用动态规划填表就可以求解上述问题

代码

#动态规划
def eggdrop(K,N):
    #建表 n行 k列  
    dp = [[float('inf')]*(K+1) for _ in range(N+1)]
    
    #初始化 楼层为1 蛋为1
    for i in range(1,K+1):#0层 和 1层
        dp[0][i] = 0
        dp[1][i] = 1
    for i in range(1,N+1):#0个蛋 和 1个蛋
        dp[i][0] = 0
        dp[i][1] = i
        
    #填表 下面代码表示先填列
    for k in range(2,K+1):#不同蛋总数
        for n in range(2,N+1):#不同楼层总数
            for t in range(1,n):
                dp[n][k] = min(dp[n][k],max(dp[t-1][k-1],dp[n-t][k])+1)
    return dp[N][K]

复杂度

时间复杂度：(O(N^2K))，三层循环

空间复杂度：(O(NK)),表的大小

注意到上述选取(T)的过程：遍历每一个楼层，计算对应的值

(M(K-1,T-1))：随T增加而增加

(M(K,N-T))：随T减小而减小

使用二分查找

#二分查找
#动态规划
def eggdrop(K,N):
    #建表 n行 k列  
    dp = [[float('inf')]*(K+1) for _ in range(N+1)]
    
    #初始化 楼层为1 蛋为1
    for i in range(1,K+1):#0层 和 1层
        dp[0][i] = 0
        dp[1][i] = 1
    for i in range(1,N+1):#0个蛋 和 1个蛋
        dp[i][0] = 0
        dp[i][1] = i
        
    #求解
    for k in range(2,K+1):#不同蛋数结果
        for n in range(2,N+1):#不同楼层数
            left = 1;
            right = n;
            while (left < right):
                mid = left + (right - left+1) // 2;
                breakCount = dp[mid - 1][k - 1]
                notBreakCount = dp[n - mid][k]
                if (breakCount > notBreakCount):
                    right = mid - 1
                else:
                    left = mid;
                dp[n][k] = min(dp[n][k],max(dp[left-1][k-1],dp[n-left][k])+1)
    return dp[N][K]

复杂度

时间复杂度：(O(KNlogN))

空间复杂度：(O(NK)),表的大小