牛客小白月赛30题解（7/10）

牛客小白月赛30题解（部分）

A.黑白边

A.黑白边

考点：并查集、最小生成树

根据题可以看出，就是一道最小生成树的裸模板题

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 2e5+10, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;
    
    bool operator < (const Edge &t) const
    {
        return w < t.w;
    }
}edges[N];
    
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
    
int kruskal()
{
    sort(edges, edges + m);
    
    for(int i = 1; i <= n; i++) p[i] = i;
    
    int res = 0, cnt = 0;
    for(int i = 0; i < m; i++)
    {
        int a = edges[i].a, b = edges[i].b, c = edges[i].w;
        
        a = find(a), b = find(b);
        if(a != b)
        {
            res += c;
            cnt++;
            p[a] = b;
        }
    }
    
    if(cnt < n-1) return INF;
    else return res;
}

int main()
{
    cin >> n >> m;
    for(int i = 0; i < m; i++) scanf("%d%d%d", &edges[i].a, &edges[i].b, &edges[i].w);
    
    int t = kruskal();
    
    if(t == INF) cout << -1 << endl;
    else cout << t << endl;
    
    return 0;
}

B.最好的宝石

B.最好的宝石

待补。。。。。。

C.滑板上楼梯

C.滑板上楼梯
考点：贪心、数学

根据题意：要使次数最少，就要尽可能多走3步；3+1为一组，除一下，然后特判最后剩余步数是否为3即可

代码：

#include <iostream>

using namespace std;

int main()
{
    long long n;
    cin >> n;

    cout << n / 4 * 2 + ((n % 4) == 3 ? 1 : n % 4) << endl;
    
    return 0;
}

D.GCD

D.GCD

考点：筛法求质数

分析题目可得：如果我们把1~n所有的质数和1全部放入子集，则任意两个数的 gcd(x, y)均等于1
故要使题意成立，需满足两个条件：
1、1~n必须有合数
2、满足1的条件下，k的最小值为 质数+2（包含1和1个合数）
解法：求出1~n所有的质数cnt，如果不等于n-1，则k = cnt+2;否则不存在输出-1

代码：

#include <iostream>

using namespace std;

const int N = 1e5+10;

int cnt, primes[N];
bool st[N];

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int main()
{
    int n;
    cin >> n;
    
    get_primes(n);
    
    if(cnt + 1 == n) cout << -1 << endl;
    else cout << cnt + 2 << endl;
    
    return 0;
}

E.牛牛的加法

E.牛牛的加法

考点：高精度加法（大数加法）、模拟

高精度加法模板题

代码：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> A, B;

vector<int> add(vector<int> A, vector<int> B)
{
	vector<int> C;
	for(int i = 0; i < A.size() || i < B.size(); i++)
	{
		int t = 0;
		if(i < A.size()) t += A[i];
		if(i < B.size()) t += B[i];
		C.push_back(t % 10);
	}
	
	return C;
}

int main()
{
	string a, b;
	cin >> a >> b;
	
	for(int i = a.size() - 1; ~i; i--) A.push_back(a[i] - '0');
	for(int i = b.size() - 1; ~i; i--) B.push_back(b[i] - '0');
	
	vector<int> C = add(A, B);
	while(C.size() > 1 && C.back() == 0) C.pop_back();
	
	for(int i = C.size() - 1; ~i; i--) cout << C[i];
 
	return 0;
 } 

F.石子合并

F.石子合并

考点：贪心

贪心，每次选最大的和其相邻的某一个，记录总和，最后加上max*(n-2)即可

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

int n;
ll ans, m;

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++) 
    {
        ll a;
        scanf("%lld", &a);
        ans += a;
        m = max(m, a);
    }
    
    cout << ans + m * (n - 2) << endl;
    
    return 0;
}

G.滑板比赛

G.滑板比赛

待补。。。。。。

H.第k小

H.第k小
考点：小根堆（优先队列）

直接用STL的优先队列priority_queue<int> q;来维护k个数即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>

using namespace std;

int n, m, k;
priority_queue<int> q;

int main()
{
    cin >> n >> m >> k;
    for(int i = 0; i < n; i++) 
    {
        int a;
        scanf("%d", &a);
        q.push(a);
    }
    
     while(m--)
     {
         int i;
         cin >> i;
         //输入一个数，直接放入优先队列
         if(i == 1)
         {
             int x;
             scanf("%d", &x);
             q.push(x);
         }
         else
         {
             //如果优先队列的大小小于k个，则输出-1
             //如果大于k个，就把优先队列开头的数弹出，直到大小为k，输出队头即可
             if(q.size() < k) printf("-1
");
             else
             {
                 while(q.size() > k) q.pop();
                 printf("%d
", q.top());
             }
         }
     }
    
    return 0;
}

I.区间异或

I.区间异或

待补。。。。。。

J.小游戏

J.小游戏

考点：动态规划

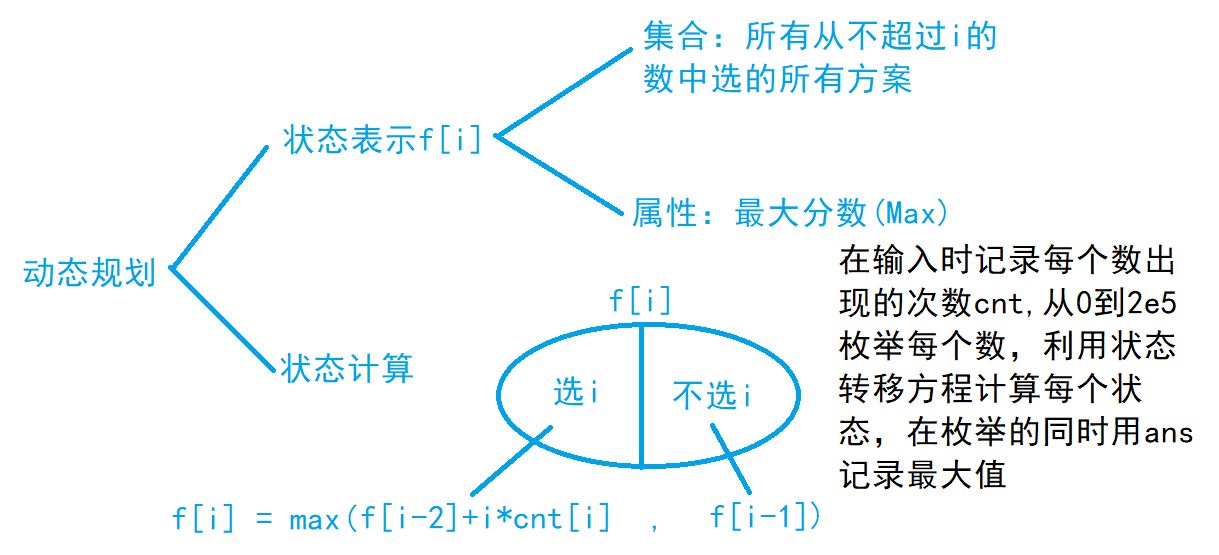
代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 2e5+10;

int n, cnt[N];
long long f[N];

int main()
{
    cin >> n;
    
    for(int i = 1; i <= n; i++)
    {
        int a;
        scanf("%d", &a);
        cnt[a]++;
    }
    
    long long ans = 0;
    for(int i = 0; i <= 2e5; i++)
    {
        f[i] = max(f[max(0,i - 1)], f[max(0, i - 2)] + i * cnt[i]);
        ans = max(ans, f[i]);
    }
    
    cout << ans << endl;
        
    return 0;
}