Given the root of a binary tree, find the maximum value V for which there exist different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.
A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.
Example 1:
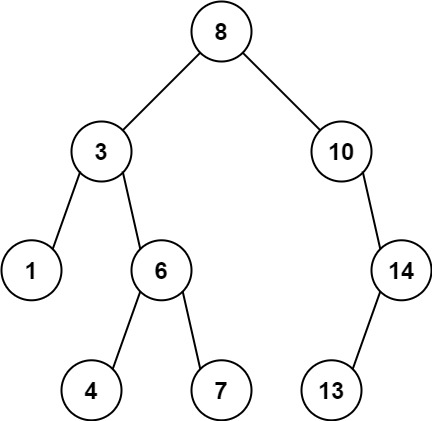
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Example 2:
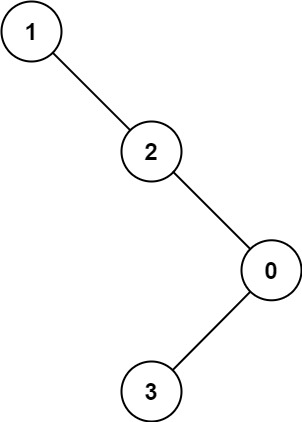
Input: root = [1,null,2,null,0,3]
Output: 3
Constraints:
- The number of nodes in the tree is in the range
[2, 5000]. 0 <= Node.val <= 105
这道题给了一棵二叉树,让找某个结点和其祖先结点最大的差的绝对值,题目中给了图很好的说明了两个结点之间的关系。注意这里并不是任意两个结点都可以做差取绝对值,必须一个要是另一个的祖先结点,这刚好符合二叉树的先序遍历的顺序,当遍历到某个结点的时候,该结点的祖先结点都已经遍历过了,但是为了找出最大的差绝对值,我们需要记录当前遍历过的祖先结点中的最大值和最小值,用它们和当前结点值做差并取绝对值,并分别更新结果 res,所以整个操作就可以直接在递归函数中进行了,参见代码如下:
解法一:
class Solution {
public:
int maxAncestorDiff(TreeNode* root) {
int res = 0;
helper(root, root->val, root->val, res);
return res;
}
void helper(TreeNode* node, int mn, int mx, int& res) {
if (!node) return;
res = max(res, abs(node->val - mn));
res = max(res, abs(mx - node->val));
mn = min(mn, node->val);
mx = max(mx, node->val);
helper(node->left, mn, mx, res);
helper(node->right, mn, mx, res);
}
};
我们也可以写的更简洁一下,用子函数的返回值当作结果 res,这样就少了一个参数了,参见代码如下:
解法二:
class Solution {
public:
int maxAncestorDiff(TreeNode* root) {
return helper(root, root->val, root->val);
}
int helper(TreeNode* node, int mn, int mx) {
if (!node) return mx - mn;
mn = min(mn, node->val);
mx = max(mx, node->val);
return max(helper(node->left, mn, mx), helper(node->right, mn, mx));
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1026
参考资料:
https://leetcode.com/problems/maximum-difference-between-node-and-ancestor/