[LeetCode] Largest Triangle Area 最大的三角区域

You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation: 
The five points are show in the figure below. The red triangle is the largest.

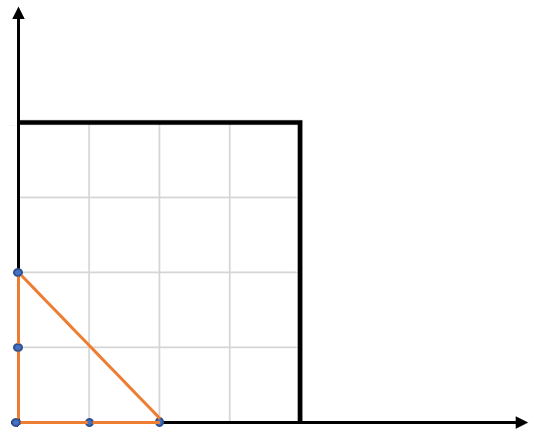
Notes:

• 3 <= points.length <= 50.
• No points will be duplicated.
•  -50 <= points[i][j] <= 50.
• Answers within 10^-6 of the true value will be accepted as correct.

这道题给了我们一系列的二维平面上的点，让我们找出任意三个点能组成的最大三角形的面积。那么我们只能遍历所有的三角形面积，然后找出最大的那个。貌似这道题也没有啥特别简便的方法，不遍历不行啊。遍历任意三个点简单，问题来了，如何通过三个顶点的坐标求出三角形面积，这个可就是初中几何题了，博主也不记得，只能上网搜一波。就是用下面这个公式即可：

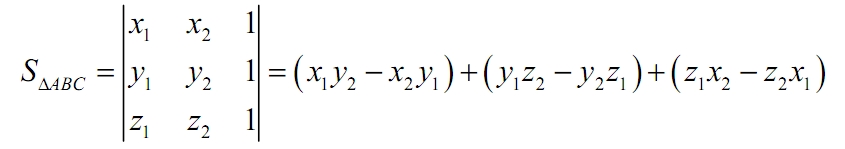
这里面三个顶点分别是(x1, y1)，(x2, y2)，(x3, y3)，有了公式后，本题就没有什么难点了，参见代码如下：

解法一：

class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        double res = 0;
        for (int i = 0; i < points.size(); ++i) {
            for (int j = i + 1; j < points.size(); ++j) {
                for (int k = j + 1; k < points.size(); ++k) {
                    int x1 = points[i][0], y1 = points[i][1];
                    int x2 = points[j][0], y2 = points[j][1];
                    int x3 = points[k][0], y3 = points[k][1];
                    double area = abs(0.5 * (x2 * y3 + x1 * y2 + x3 * y1 - x3 * y2 - x2 * y1 - x1 * y3));
                    res = max(res, area);
                }
            }
        }
        return res;
    }
};

我们也可以稍稍简化一下上面的写法，但是解题思路没有任何区别，参见代码如下：

解法二：

class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        double res = 0;
        for (auto &i : points) {
            for (auto &j : points) {
                for (auto &k : points) {
                    res = max(res, 0.5 * abs(i[0] * j[1] + j[0] * k[1] + k[0] * i[1]- j[0] * i[1] - k[0] * j[1] - i[0] * k[1]));
                }
            }
        }
        return res;
    }
};

参考资料：

https://leetcode.com/problems/largest-triangle-area/discuss/122711/C++JavaPython-Solution-with-Explanation-and-Prove

LeetCode All in One 题目讲解汇总(持续更新中...)