读《An Adaptable and Extensible Geometry Kernel》
利用Curiously Recurring Template Pattern替代虚函数
详细内容可以参考[1]。这里单纯列举出相关的代码示例:
// 使用继承的方式实现不同图形的绘制
class Shape
{
public:
Shape() {}
virtual ~Shape() {}
virtual void Draw() = 0;
};
class Triangle : public Shape
{
public:
Triangle() {}
~Triangle() {}
void Draw() { cout << "Draw a Triangle" << endl; }
};
class Rectangle : public Shape
{
public:
Rectangle() {}
~Rectangle() {}
void Draw() { cout << "Draw a Rectangle" << endl; }
};
// 利用Curiously Recurring Template Pattern
template <typename Derived>
class Shape
{
public:
void Draw()
{
return static_cast<Derived*>(this)->Draw();
}
};
class Triangle : public Shape<Triangle>
{
public:
void Draw() { cout << "Draw a Triangle" << endl; }
};
class Rectangle : public Shape<Rectangle>
{
public:
void Draw() { cout << "Draw a Rectangle" << endl; }
};
为什么需要Kernel
通过Kernel需要解决的主要问题是代码的适配性和可扩展性。那为什么可以提高适配性和可扩展性可以在后续的内容中得到答案。
Kernel的概念和架构
常见的数据结构和算法的设计,数据结构为独立的类,算法为全局或类的成员函数。示例如下:
K::Point_2 p(0,1), q(1,-4); // 数据结构
K::Line_2 line(p,q);
if (less_xy_2(p, q)) { ... } // 算法成员函数
几何Kernel包含需要操作的类型,以及针对这些类型的操作。Kernel会将上述相关的内容进行打包处理。示例如下:
K k;
K::Construct_line_2 c_line = k.construct_line_2_object();
K::Less_xy_2 less_xy = k.less_xy_2_object();
K::Point_2 p(0,1), q(1,-4);
K::Line_2 line = c_line(p, q);
if (less_xy(p, q)) { ... }
Kernel将数据结构和算法相关的细节放到了内部。整体的架构可以分为三层,Kernel, Geometric Primitives,Numeric Primitives,具体如下:
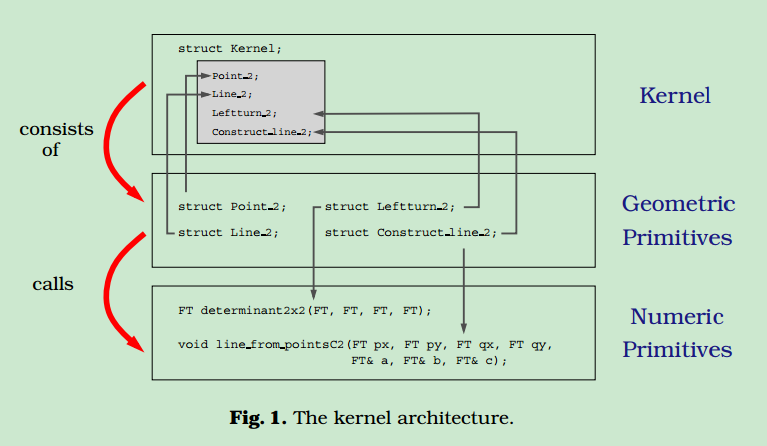
Kernel的实现
第一版本
template <class K> struct MyPoint { };
template <class K> struct MyLine { };
template <class K> struct MyConstruct { };
template <class K> struct MyLess { };
struct Kernel {
typedef MyPoint<Kernel> Point_2;
typedef MyLine<Kernel> Line_2;
typedef MyConstruct<Kernel> Construct_line_2;
typedef MyLess<Kernel> Less_xy_2;
};
// Generate new Kernel
template <class K> struct NewPoint { };
template <class K> struct MyLeftTurn { };
struct New_kernel : public Kernel {
typedef NewPoint<New_kernel> Point_2;
typedef MyLeftTurn<New_kernel> Left_turn_2;
};
int main()
{
New_kernel::Point_2 p, q;
New_kernel::Construct_line_2 construct_line_2;
New_kernel::Line_2 l = construct_line_2(p, q);
return 0;
}
测试环境可以见: https://ideone.com/MrXCDD
编译错误为:
prog.cpp: In function ‘int main()’:
prog.cpp:28:49: error: no match for call to ‘(Kernel::Construct_line_2 {aka MyConstruct<Kernel>}) (New_kernel::Point_2&, New_kernel::Point_2&)’
New_kernel::Line_2 l = construct_line_2(p, q);
从编译错误中可见,New_kernel::Construct_line_2其实调用的是MyConstruct<Kernel>的实现,而我们想要的调用是MyConstruct<New_kernel>。依赖关系见下图:
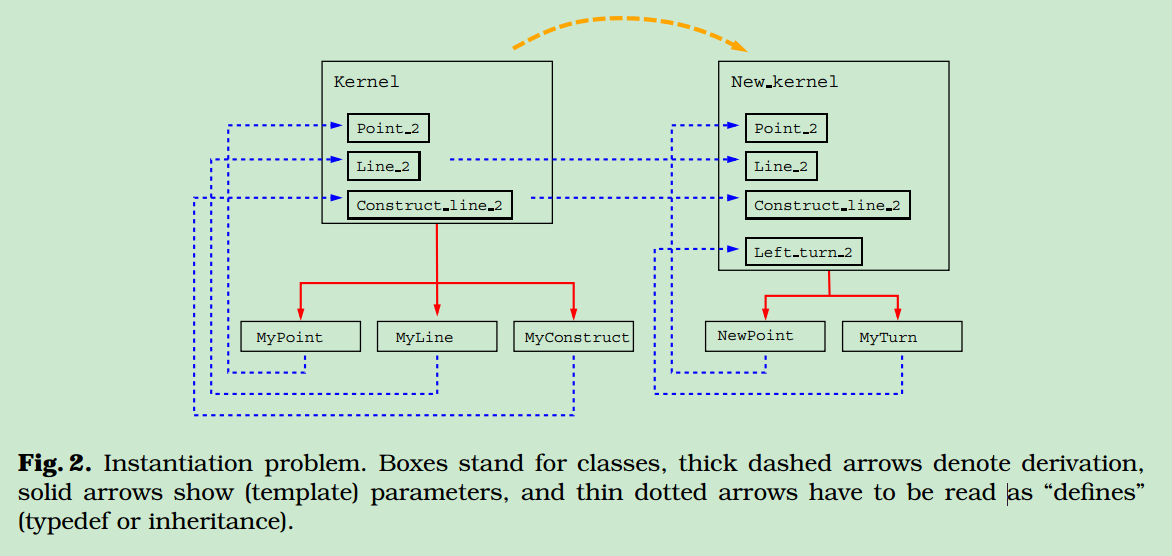
这个版本中另一个隐含的问题是,循环引用的问题,具体如下:
template <class K> struct P {
typedef K::A B;
};
struct Kernel {
typedef P<Kernel>::B B;
typedef int A;
};
为了解决上面的问题,进行了第二版本的改进。
第二版本
为了降低不同Kernel之间的关联性,引入Kernel_base,具体如下:
template <class K> struct MyPoint { };
template <class K> struct MyLine { };
template <class K> struct MyConstruct { };
template <class K> struct MyLess { };
template <class K>
struct Kernel_base {
typedef MyPoint<K> Point_2;
typedef MyLine<K> Line_2;
typedef MyConstruct<K> Construct_line_2;
typedef MyLess<K> Less_xy_2;
};
struct Kernel : public Kernel_base<Kernel> { };
// Generate new Kernel
template <class K> struct NewPoint { };
template <class K> struct MyLeftTurn { };
template<class K>
struct New_kernel_base : public Kernel_base<K> {
typedef NewPoint<K> Point_2;
typedef MyLeftTurn<K> Left_turn_2;
};
struct New_kernel : public New_kernel_base<New_kernel> {};
int main()
{
New_kernel::Point_2 p, q;
New_kernel::Construct_line_2 construct_line_2;
New_kernel::Line_2 l = construct_line_2(p, q);
return 0;
}
测试环境可以见:https://ideone.com/40wOCa
编译错误如下:
prog.cpp: In function ‘int main()’:
prog.cpp:35:49: error: no match for call to ‘(Kernel_base<New_kernel>::Construct_line_2 {aka MyConstruct<New_kernel>}) (New_kernel_base<New_kernel>::Point_2&, New_kernel_base<New_kernel>::Point_2&)’
New_kernel::Line_2 l = construct_line_2(p, q);
^
从编译结果中可得,Construct_line_2对应的New_kernel正是我们所预期的。接下来需要解决的问题是,construct_line_2并不是可以调用的函数。调整后kernel之间的依赖关系如下:

第三版本
该版本中,利用函数对象来处理操作逻辑。
template <class K> struct MyPoint { };
template <class K> struct MyLine { };
template <class K> struct MyConstruct {
typedef typename K::Line_2 Line_2;
typedef typename K::Point_2 Point_2;
Line_2 operator() (Point_2, Point_2) const
{
return Line_2();
}
};
template <class K> struct MyLess {
typedef typename K::Point_2 Point_2;
bool operator() (Point_2, Point_2) const
{
return true;
}
};
template <class K>
struct Kernel_base {
typedef MyPoint<K> Point_2;
typedef MyLine<K> Line_2;
typedef MyConstruct<K> Construct_line_2;
typedef MyLess<K> Less_xy_2;
Construct_line_2 construct_line_2_object();
Less_xy_2 less_xy_2_object();
};
struct Kernel : public Kernel_base<Kernel> { };
// Generate new Kernel
template <class K> struct NewPoint { };
template <class K> struct MyLeftTurn { };
template<class K>
struct New_kernel_base : public Kernel_base<K> {
typedef NewPoint<K> Point_2;
typedef MyLeftTurn<K> Left_turn_2;
};
struct New_kernel : public New_kernel_base<New_kernel> {};
int main()
{
New_kernel::Point_2 p, q;
New_kernel::Construct_line_2 construct_line_2;
New_kernel::Line_2 l = construct_line_2(p, q);
return 0;
}
示例程序见:https://ideone.com/6ISelp
整个编译过程成功通过。
到此处,整个kernel的结构基本完善了。
Kernel使用示例说明算法的适应性
以2D点集凸包计算的实现来举例:https://doc.cgal.org/latest/Convex_hull_2/index.html。仅仅针对算法实现过程中Kernel的使用进行简单说明,对算法的具体实现此处不进行介绍。
// 暴露给外部调用的接口
template <class InputIterator, class OutputIterator>
inline
OutputIterator
ch_graham_andrew( InputIterator first,
InputIterator last,
OutputIterator result)
{
typedef std::iterator_traits<InputIterator> ITraits;
typedef typename ITraits::value_type value_type;
typedef CGAL::Kernel_traits<value_type> KTraits; // 根据value_type获取KernelTraits
typedef typename KTraits::Kernel Kernel; // 进一步获取Kernel
return ch_graham_andrew(first, last, result, Kernel()); // 传入Kernel,调用具体实现
}
// 具体实现
template <class InputIterator, class OutputIterator, class Traits>
OutputIterator
ch_graham_andrew( InputIterator first,
InputIterator last,
OutputIterator result,
const Traits& ch_traits)
{
typedef typename Traits::Point_2 Point_2; // 获取Kernel中的类型
typedef typename Traits::Equal_2 Equal_2; // 获取Kernel中的类型
Equal_2 equal_points = ch_traits.equal_2_object(); // 获取kernel中的算法
if (first == last) return result;
std::vector< Point_2 > V (first, last);
std::sort( V.begin(), V.end(), ch_traits.less_xy_2_object() ); // 获取Kernel中的算法
if (equal_points( *(V.begin()), *(V.rbegin())) )
{
*result++ = *(V.begin());
return result;
}
#if defined(CGAL_CH_NO_POSTCONDITIONS) || defined(CGAL_NO_POSTCONDITIONS)
|| defined(NDEBUG)
OutputIterator res(result);
#else
Tee_for_output_iterator<OutputIterator,Point_2> res(result);
#endif // no postconditions ...
ch__ref_graham_andrew_scan( V.begin(), V.end(), res, ch_traits);
ch__ref_graham_andrew_scan( V.rbegin(), V.rend(), res, ch_traits);
CGAL_ch_postcondition(
is_ccw_strongly_convex_2( res.output_so_far_begin(),
res.output_so_far_end(),
ch_traits));
CGAL_ch_expensive_postcondition(
ch_brute_force_check_2(
V.begin(), V.end(),
res.output_so_far_begin(), res.output_so_far_end(),
ch_traits));
#if defined(CGAL_CH_NO_POSTCONDITIONS) || defined(CGAL_NO_POSTCONDITIONS)
|| defined(NDEBUG)
return res;
#else
return res.to_output_iterator();
#endif // no postconditions ...
}
从上面简单的示例可得,一般在算法构建的时候会在最外层生成调用接口,然后,在具体实现中,通过分别对Kernel中的数据结构和算法的调用,最后组装成一个完整的算法实现。
简单的完整的Kernel
此处将文章最后的示例代码贴出来,用于进一步完善对Kernel的认知。
//------------------------------------------------------------
// bottom layer: number type based function toolbox
//
template <class FT>
FT determinant2x2(FT a00, FT a01, FT a10, FT a11)
{
return a00*a11 - a10*a01;
}
template <class FT>
void line_from_pointsC2(FT px, FT py, FT qx, FT qy, FT &a, FT &b, FT &c) {}
//------------------------------------------------------------
// mid layer: representations, predicates and constructions
//
template <class K_>
struct Point_2 {
typedef K_ K;
typedef typename K::FT FT;
Point_2() {}
Point_2(FT x_, FT y_) : x(x_), y(y_) {}
FT x, y;
};
template <class K_>
struct Line_2 {
typedef K_ K;
typedef typename K::Point_2 Point_2;
Line_2() {}
Line_2(Point_2 p, Point_2 q) { *this = K::Construct_line_2(p,q); }
typename K::FT a, b, c;
};
template <class K_>
struct Segment_2 {
typedef K_ K;
typename K::Point_2 s, e;
};
template <class K_>
struct Less_xy_2 {
typedef typename K_::Point_2 Point_2;
bool operator()(Point_2 p, Point_2 q) const
{ return p.x < q.x || p.x == q.x && p.y < q.y; }
};
template <class K_>
struct Left_turn_2 {
typedef typename K_::Point_2 Point_2;
bool operator()(Point_2 p, Point_2 q, Point_2 r) const
{
return determinant2x2(q.x - p.x, q.y - p.y,
r.x - p.x, r.y - q.y) > 0;
}
};
template <class K_>
struct Construct_line_2 {
typedef typename K_::Point_2 Point_2;
typedef typename K_::Line_2 Line_2;
Line_2 operator()(Point_2 p, Point_2 q) const {
Line_2 l;
Line_from_pointsC2(p.x, p.y, q.x, q.y, l.a, l.b, l.c);
return l;
}
};
//------------------------------------------------------------
// top layer: geometric kernel
//
template <class K_, class FT_>
struct Kernel_bae {
typedef K_ K;
typedef FT_ FT;
typedef Point_2<K> Point_2;
typedef Line_2<K> Line_2;
typedef Segment_2<K> Segment_2;
typedef Less_xy_2<K> Less_xy_2;
typedef Left_turn_2<K> Left_turn_2;
typedef Construct_line_2<K> Construct_line_2;
Less_xy_2 less_xy_2_object() const { return Less_xy_2(); }
Left_turn_2 Left_turn_2_object() const { return Left_turn_2(); }
Construct_line_2 construct_line_2_object() const { return Construct_line_2(); }
};
template <class FT_>
struct Kernel : public Kernel_base<Kernel<FT_>, FT_>
{};
//------------------------------------------------------------
// convenience layer: global functions
//
template < class K >inline
bool
less_xy_2(typename K::Point_2 p,typename K::Point_2 q, K k = K())
{ returnk.less_xy_2_object()(p, q); }
template < class K >inline
bool
left_turn_2(typenameK::Point_2 p,
typenameK::Point_2 q,
typenameK::Point_2 r,
K k = K())
{ returnk.left_turn_2_object()(p, q, r); }
//------------------------------------------------------------
// enve more convenience: specializations for kernel
//
template < class FT > inline
bool
left_turn_2(Point_2< Kernel< FT > > p,
Point_2< Kernel< FT > > q,
Point_2< Kernel< FT > > r)
{ returnleft_turn_2(p, q, r, Kernel< FT >()); }
template < class FT >inline
bool
less_xy_2(Point_2< Kernel< FT > > p, Point_2< Kernel< FT > > q)
{ returnless_xy_2(p, q, Kernel< FT >()); }
参考
- [1] https://www.geeksforgeeks.org/curiously-recurring-template-pattern-crtp-2/
- [2] An Adaptable and Extensible Geometry Kernel https://inf.ethz.ch/~hoffmann/pub/hhkps-aegk-01a.pdf