GCompute

GCompute - 计算三角形对的交点（1）

本文是利用论文中的介绍进行实现的.

Moller T. A fast triangle-triangle intersection test[J]. Journal of Graphics Tools, 1997, 2(2): 25-30.

https://cn.bing.com/academic/profile?id=8f3b04bb774f7be38107ff2d63d056b5&encoded=0&v=paper_preview&mkt=zh-cn#

关于该论文的介绍参见：PaperRead - A fast triangle-triangle intersection test

基于该论文的相交测试实现，参见：PaperImpl - A fast triangle-triangle intersection test

三角形交点计算原理

论文介绍一文中分析如下：

直线L与三角形，相交段计算。假设我们需要计算三角形(T_1)和直线(L)之间的相交线段，假设(V_0^1)和(V_2^1)位于平面(pi_2)的同一侧，(V_1^1)位于平面的另一侧。先将顶点投影到直线L上，如下：

[p_{V_i^1} = Dcdot (V_i^1 - O) ]

论文中经过优化有，(p_{V_i^1})的计算公式如下：

[p_{V_i^1} = left{egin{array}{rcl}V_{ix}^1, if |D_x| = max(|D_x|, |D_y|, |D_z|) \V_{iy}^1, if |D_y| = max(|D_x|, |D_y|, |D_z|) \V_{iz}^1, if |D_z| = max(|D_x|, |D_y|, |D_z|) \end{array}, i=0,1,2. ight. ]

然后进一步计算t点，如下：

[t_1 = p_{V_0^1} + (p_{V_1^1} - p_{V_0^1})frac{d_{V_0^1}}{d_{V_0^1} - d_{V_1^1}} ]

此时计算出来的t值，就是在交点在(max(|D_x|,|D_y|,|D_z|))对应轴上的值。然后再将该值带入两个三角形的平面方程，就可以求得交点的具体坐标。

源码实现

具体实现在之前相交测试代码的基础上，增加了两个平面相交求解的过程。完整代码如下：

#pragma once

#include <iostream>
#include <cmath>
#include <algorithm>
#include <assert.h>
#include <vector>

#include <Eigen/Dense>

typedef Eigen::Vector3d Point3d;

class Triangle 
{
public:
    Triangle(Point3d pt0, Point3d pt1, Point3d pt2) : m_pt {pt0, pt1, pt2} 
    {
        auto vecPt0TPt1 = pt1 - pt0;
        auto vecPt0TPt2 = pt2 - pt0;
        m_vecNormal = vecPt0TPt1.cross(vecPt0TPt2);
        m_vecNormal.normalize();
    }

    double GetDistanceFromPointToTrianglePlane(Point3d pt) const
    {
        auto vecPtTPt0 = m_pt[0] - pt;
        
        return m_vecNormal.dot(vecPtTPt0);
    }

    void GetTriangleVertices(Point3d (&pt)[3]) const
    {
        pt[0] = m_pt[0];
        pt[1] = m_pt[1];
        pt[2] = m_pt[2];
    }

    void GetNormal(Eigen::Vector3d &vecNormal) const
    {
        vecNormal = m_vecNormal;
    }

private:
    Point3d m_pt[3];
    Eigen::Vector3d m_vecNormal;
};


#define EPSION 1e-7

enum IntersectionType
{
    INTERSECTION,             //< 有相交线段
    DISJOINT,                 //< 不相交
    COPLANE                   //< 共面
};

bool IsZero(double value, double epsion = EPSION)
{
    return std::abs(value) < epsion;
}

bool IsEqual(double v1, double v2, double epsion = EPSION)
{
    return IsZero(v1-v2, epsion);
}

bool IsPositive(double value, double epsion = EPSION)
{
    return value - epsion > 0;
}

bool IsNegative(double value, double epsion = EPSION)
{
    return value + epsion < 0;
}

int GetSignType(double value)
{
    if (IsZero(value)) return 0;
    if (IsPositive(value)) return 1;
    return -1;
}

template<typename T>
void Swap(T &a, T &b)
{
    auto tmp = a;
    a = b;
    b = tmp;
}

void GetVertexNewOrder(const int (&disVTri1SignType)[3], const double (&disVTri1TPlaneTri2)[3], int (&vertexTri1NewOrder)[3])
{
    // 将顶点划分成两部分，0,2位于另一个三角形同一侧，1位于另一个三角形另一侧
    vertexTri1NewOrder[0] = 0;
    vertexTri1NewOrder[1] = 1;
    vertexTri1NewOrder[2] = 2;

    int prodValue = disVTri1SignType[0] * disVTri1SignType[1] * disVTri1SignType[2];
    // 如果乘积<0，则小于0的为单独的点
    if (prodValue < 0) {
        for (int i = 0; i < 3; ++i) {
            if (disVTri1TPlaneTri2[i] < 0) {
                Swap(vertexTri1NewOrder[i], vertexTri1NewOrder[1]);
                break;
            }
        }
    }
    // 如果乘积>0，则大于0的为单独的点
    else if (prodValue > 0) {
        for (int i = 0; i < 3; ++i) {
            if (disVTri1TPlaneTri2[i] > 0) {
                Swap(vertexTri1NewOrder[i], vertexTri1NewOrder[1]);
                break;
            }
        }
    }
    // 有点位于平面上
    else {
        int sumValue = disVTri1SignType[0] + disVTri1SignType[1] + disVTri1SignType[2];
        // 如果只有一个点等于0，并且另外两个点同号，那么等于0的点为单独的点
        if (std::abs(sumValue) == 2) {
            for (int i = 0; i < 3; ++i) {
                if (disVTri1TPlaneTri2[i] == 0) {
                    Swap(vertexTri1NewOrder[i], vertexTri1NewOrder[1]);
                    break;
                }
            }
        }
        // 如果只有一个点等于0，并且另外两个点异号，那么假定小于0的点为单独的点
        else if (std::abs(sumValue) == 0) {
            for (int i = 0; i < 3; ++i) {
                if (disVTri1TPlaneTri2[i] < 0) {
                    Swap(vertexTri1NewOrder[i], vertexTri1NewOrder[1]);
                    break;
                }
            }
        }
        // 如果两个点等于0，那么不等于0的点为单独的点
        else {
            for (int i = 0; i < 3; ++i) {
                if (disVTri1TPlaneTri2[i] != 0) {
                    Swap(vertexTri1NewOrder[i], vertexTri1NewOrder[1]);
                    break;
                }
            }
        }
    }
}

void CalculateT(
    const Eigen::Vector3d& vecNormalTri1,
    const double(&disVTri1TPlaneTri2)[3], 
    const int (&vertexTri1NewOrder)[3], 
    const Point3d (&verticesTri1)[3], 
    double (&tTri1)[2],
    int& whichAxis)
{

    int maxValueIndex = 0;;
    double maxValue = vecNormalTri1[0];
    for (int i = 1; i < 3; ++i) {
        if (maxValue < vecNormalTri1[i]) {
            maxValue = vecNormalTri1[i];
            maxValueIndex = i;
        }
    }

    double pTri1OnLine[3] = {
        verticesTri1[vertexTri1NewOrder[0]](maxValueIndex),
        verticesTri1[vertexTri1NewOrder[1]](maxValueIndex),
        verticesTri1[vertexTri1NewOrder[2]](maxValueIndex) };

    tTri1[0] = pTri1OnLine[0] +
        (pTri1OnLine[1] - pTri1OnLine[0]) *
        disVTri1TPlaneTri2[vertexTri1NewOrder[0]] /
        (disVTri1TPlaneTri2[vertexTri1NewOrder[0]] - disVTri1TPlaneTri2[vertexTri1NewOrder[1]]);
    tTri1[1] = pTri1OnLine[2] +
        (pTri1OnLine[1] - pTri1OnLine[2]) *
        disVTri1TPlaneTri2[vertexTri1NewOrder[2]] /
        (disVTri1TPlaneTri2[vertexTri1NewOrder[2]] - disVTri1TPlaneTri2[vertexTri1NewOrder[1]]);
    
    whichAxis = maxValueIndex;
}

void CalculateIntersectionPoint(
    const Triangle& tri1, const Triangle& tri2,
    double t, int axisIndex, std::vector<Point3d>& interPts)
{
    // function:
    // N1_x(P_x - V1_x) + N1_y(P_y - V1_y) + N1_z(P_z - V1_z) = 0
    // N2_x(P_x - V2_x) + N2_y(P_y - V2_y) + N2_z(P_z - V2_z) = 0
    // =>
    // N1_xP_x + N1_yP_y + N1_zP_z = N1 cdot V1
    // N2_xP_x + N2_yP_y + N2_zP_z = N2 cdot V2
    // N: the normal of triangle
    // V: the point on triangle
    Eigen::Vector3d vecNormal1;
    tri1.GetNormal(vecNormal1);
    Point3d pts1[3];
    tri1.GetTriangleVertices(pts1);
    Point3d ptV1 = pts1[0];
    double d1 = vecNormal1.dot(ptV1);

    Eigen::Vector3d vecNormal2;
    tri2.GetNormal(vecNormal2);
    Point3d pts2[3];
    tri2.GetTriangleVertices(pts2);
    Point3d ptV2 = pts2[0];
    double d2 = vecNormal2.dot(ptV2);

    Point3d ptIntersect;
    if (axisIndex == 0) // x
    {
        ptIntersect[0] = t;
        // N1_yP_y + N1_zP_z = d1 - N1_x t
        // N2_yP_y + N2_zP_z = d2 - N2_x t
        double determinant = vecNormal1.y() * vecNormal2.z() - vecNormal1.z() * vecNormal2.y();
        double determinantY = (d1 - vecNormal1.x()*t) * vecNormal2.z() - vecNormal1.z() * (d2 - vecNormal2.x()*t);
        double determinantZ = vecNormal1.y() * (d2 - vecNormal2.x()*t) - (d1 - vecNormal1.x()*t) * vecNormal2.y();
        ptIntersect[1] = determinantY / determinant;
        ptIntersect[2] = determinantZ / determinant;
    }
    else if (axisIndex == 1) // y
    {
        ptIntersect[1] = t;
        // N1_xP_x + N1_zP_z = d1 - N1_y t
        // N2_xP_x + N2_zP_z = d2 - N2_y t
        double determinant = vecNormal1.x() * vecNormal2.z() - vecNormal1.z() * vecNormal2.x();
        double determinantX = (d1 - vecNormal1.y()*t) * vecNormal2.z() - vecNormal1.z() * (d2 - vecNormal2.y()*t);
        double determinantZ = vecNormal1.x() * (d2 - vecNormal2.y()*t) - (d1 - vecNormal1.y()*t) * vecNormal2.x();
        ptIntersect[0] = determinantX / determinant;
        ptIntersect[2] = determinantZ / determinant;
    }
    else // z
    {
        ptIntersect[2] = t;
        // N1_xP_x + N1_yP_y = d1 - N1_z t
        // N2_xP_x + N2_yP_y = d2 - N2_z t
        double determinant = vecNormal1.x() * vecNormal2.y() - vecNormal1.y() * vecNormal2.x();
        double determinantX = (d1 - vecNormal1.z()*t) * vecNormal2.y() - vecNormal1.y() * (d2 - vecNormal2.z()*t);
        double determinantY = vecNormal1.x() * (d2 - vecNormal2.z()*t) - (d1 - vecNormal1.z()*t) * vecNormal2.x();
        ptIntersect[0] = determinantX / determinant;
        ptIntersect[1] = determinantY / determinant;
    }

    interPts.push_back(ptIntersect);
}

void CalculateIntersectionPoints(
    const Triangle& tri1, const Triangle& tri2, 
    double (&tTri1)[2], double (&tTri2)[2], 
    int t1Index, int t2Index, std::vector<Point3d>& interPts)
{
    // tTri1[0] tTri2[0] tTri1[1] tTri2[1]
    if (tTri1[0] < tTri2[0] && tTri2[0] < tTri1[1] && tTri1[1] < tTri2[1])
    {
        CalculateIntersectionPoint(tri1, tri2, tTri2[0], t2Index, interPts);
        CalculateIntersectionPoint(tri1, tri2, tTri1[1], t1Index, interPts);
    }
    // tTri1[0] tTri2[0] tTri2[1] tTri1[1] 
    else if (tTri1[0] < tTri2[0] && tTri2[0] < tTri2[1] && tTri2[1] < tTri1[1])
    {
        CalculateIntersectionPoint(tri1, tri2, tTri2[0], t2Index, interPts);
        CalculateIntersectionPoint(tri1, tri2, tTri2[1], t2Index, interPts);
    }
    // tTri2[0] tTri1[0] tTri1[1] tTri2[1] 
    else if (tTri2[0] < tTri1[0] && tTri1[0] < tTri1[1] && tTri1[1] < tTri2[1])
    {
        CalculateIntersectionPoint(tri1, tri2, tTri1[0], t1Index, interPts);
        CalculateIntersectionPoint(tri1, tri2, tTri1[1], t1Index, interPts);
    }
    // tTri2[0] tTri1[0] tTri2[1] tTri1[1] 
    else
    {
        CalculateIntersectionPoint(tri1, tri2, tTri1[0], t1Index, interPts);
        CalculateIntersectionPoint(tri1, tri2, tTri2[1], t2Index, interPts);
    }
}

IntersectionType TriangleIntersectionTest(const Triangle& tri1, const Triangle& tri2, std::vector<Point3d>& interPts)
{
    Point3d verticesTri1[3], verticesTri2[3];
    tri1.GetTriangleVertices(verticesTri1);
    tri2.GetTriangleVertices(verticesTri2);

    double disVTri2TPlaneTri1[3];
    int disVTri2SignType[3];
    double disVTri1TPlaneTri2[3];
    int disVTri1SignType[3];

    for (int i = 0; i < 3; ++i) {
        disVTri2TPlaneTri1[i] = tri1.GetDistanceFromPointToTrianglePlane(verticesTri2[i]);
        disVTri2SignType[i] = GetSignType(disVTri2TPlaneTri1[i]);
    }

    // 如果三角形Tri2的三个顶点在三角形Tri1的同一侧，则不相交
    if ((disVTri2SignType[0] > 0 && disVTri2SignType[1] > 0 && disVTri2SignType[2] > 0) ||
        (disVTri2SignType[0] < 0 && disVTri2SignType[1] < 0 && disVTri2SignType[2] < 0)) {
        return DISJOINT;
    }
    
    // 都为0，则共面
    if ((disVTri2SignType[0] | disVTri2SignType[1] | disVTri2SignType[2]) == 0) {
        return COPLANE;
    }
    
    for (int i = 0; i < 3; ++i) {
        disVTri1TPlaneTri2[i] = tri2.GetDistanceFromPointToTrianglePlane(verticesTri1[i]);
        disVTri1SignType[i] = GetSignType(disVTri1TPlaneTri2[i]);
    }

    // 如果三角形Tri1的三个顶点在三角形Tri2的同一侧，则不相交
    if ((disVTri1SignType[0] > 0 && disVTri1SignType[1] > 0 && disVTri1SignType[2] > 0) ||
        (disVTri1SignType[0] < 0 && disVTri1SignType[1] < 0 && disVTri1SignType[2] < 0)) {
        return DISJOINT;
    }

    // 都为0，则共面
    if ((disVTri1SignType[0] | disVTri1SignType[1] | disVTri1SignType[2]) == 0) {
        return COPLANE;
    }

    // 对顶点顺序进行调整，如何论文中的描述
    int vertexTri1NewOrder[3] = { 0, 1, 2 };
    int vertexTri2NewOrder[3] = { 0, 1, 2 };
    GetVertexNewOrder(disVTri1SignType, disVTri1TPlaneTri2, vertexTri1NewOrder);
    GetVertexNewOrder(disVTri2SignType, disVTri2TPlaneTri1, vertexTri2NewOrder);

    Eigen::Vector3d vecNormalTri1, vecNormalTri2;
    tri1.GetNormal(vecNormalTri1);
    tri2.GetNormal(vecNormalTri2);

    double tTri1[2], tTri2[2];
    int t1Index, t2Index;
    // 计算相交线和每个三角形的相交线段
    CalculateT(vecNormalTri1, disVTri1TPlaneTri2, vertexTri1NewOrder, verticesTri1, tTri1, t1Index);
    CalculateT(vecNormalTri2, disVTri2TPlaneTri1, vertexTri2NewOrder, verticesTri2, tTri2, t2Index);



    if (tTri1[0] > tTri1[1]) Swap(tTri1[0], tTri1[1]);
    if (tTri2[0] > tTri2[1]) Swap(tTri2[0], tTri2[1]);

    // 比较是否overlap
    if ((tTri2[0] > tTri1[0] && tTri2[0] < tTri1[1]) ||
        (tTri2[1] > tTri1[0] && tTri2[1] < tTri1[1])) {

        CalculateIntersectionPoints(tri1, tri2, tTri1, tTri2, t1Index, t2Index, interPts);
        
        return INTERSECTION;
    }

    return DISJOINT;
}

void TriIntersectTestCase()
{
    {
        Triangle tr1(Point3d(0, 0, 0), Point3d(1, 0, 1), Point3d(0, 1, 1));
        Triangle tr2(Point3d(1, 1, 0), Point3d(1, 1, 1), Point3d(0, 0, 1));

        std::vector<Point3d> pts;
        auto type = TriangleIntersectionTest(tr1, tr2, pts);

        assert(type == INTERSECTION);
        std::cout << "Intersection points: 
";
        for (int i = 0; i < pts.size(); ++i)
        {
            std::cout << "=====" << "
";
            std::cout << pts[i] << "
";
        }
    }
}

int main()
{
    TriIntersectTestCase();
    return 0;
}

测试结果如下：

Intersection points:
=====
0.333333
0.333333
0.666667
=====
0.5
0.5
  1

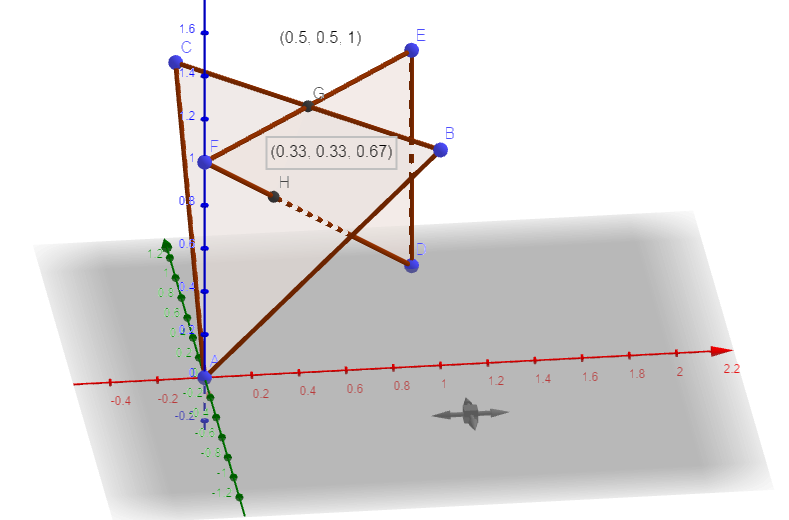
用geogebra绘图验证，如下图所示：