PaperRead - Efficient Booleans algorithms for triangulated meshes of geometric modeling
Jiang X, Peng Q, Cheng X, et al. Efficient Booleans algorithms for triangulated meshes of geometric modeling[J]. Computer-aided Design and Applications, 2016, 13(4): 419-430.
更多introduction的介绍可以直接看原文,这里主要介绍文中使用的具体实现。
2. Methods
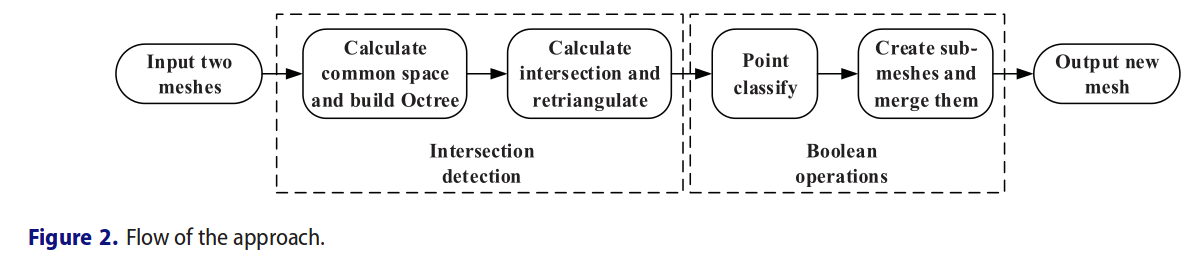
更个过程分为两个阶段:两个mesh之间的相交检测和布尔运算。如下图Fig2。
这篇文章的主要贡献点如下:
- 利用八叉树对两个网格的公共空间进行划分,以加快交叉点检测的速度,减少内存占用;
- 分析了浮点运算误差和交叉口奇异性,提高了算法的稳定性;
- 为了实现并、交、差运算,提出了基于相交三角形的稳定技术。该方法对封闭网格和开放网格都是快速的;
- 该算法具有较强的鲁棒性,可用于含有大量布尔差分运算的铣削仿真系统中;
2.1 相交检测
相交检测在布尔运算中是很重要的一布。

2.1.1 Building Octree of the common space
对于两个相交的mesh而言,相交部分的空间的大小是小的。octree能够利用空间划分加速相交测试。
给定两个网格(S_A)和(S_B)。(Box_A)和(Box_B)分别为(S_A)和(S_B)的最小AABB。公式如下:
(Box_B)可以用相同方式计算。两个的交集如下:
为了保证能够把相交三角形都包含在内部,对上面的式子进行了扩展,如下:
其中(l)为(S_A)和(S_B)中的最长边。
2.1.2 Floating point arithmetic errors and singularity of intersections
这一节主要介绍了浮点型计算精度引发的一些问题。
2.1.3 计算相交线
相交线计算的时候需要考虑两种情况,共面还是不共面,针对共面问题,可以转换为2D 三角形相交问题。这里主要介绍不共面时候相交线的计算。
通常情况下,有三种相交情况(如下图所示):
- 交点为顶点,EndP;
- 在边上有一个检点,EdgeP;
- 面内有一个交点,FaceP;

三种交点的权重比为:EndP > EdgeP > FaceP。
算法的详细伪代码如下:
Algorithm 1 Calculate intersection lines
for each pair of triangles (T1, T2) do
for each edge e in T1 do
m = Intersection(e, T2);
if (exist_intersection(e, T2) && m* = Intersection(e, T2))
Properties(m) = Properties(m*) = Priority(m,m*)
Coordinate(m*) = Coordinate(m)
end for
for each edge e in T2 do
m = Intersection(e, T1)
if (exist_intersection(e, T1) && m* = Intersection(e, T1))
Properties(m) = Properties(m*) = Priority(m,m*)
Coordinate(m*) = Coordinate(m)
end for
end for
2.1.4. 对相交三角形重新三角化
相交的三角形上,通常会有多个相交线段,这些相交线段将三角形划分为多个多边形面。(如何划分??)接下来这些多边形需要被三角化。
- Recursive ear cutting algorithm很简单容易实现,但是性能比较差,不容易扩展处理空洞的情况;
- incremental randomized算法,性能不错,但不容易实现;
- sweep line算法是当前使用最广泛的实现,文中采用了Poly2Tri(Wu L.: Poly2Tri: Fast and Robust Simple Polygon Trian-gulation With/ Without Holes by Sweep Line Algorithm,http://sites-final.uclouvain.be/mema/Poly2Tri/, 2005.),相关代码实现:https://github.com/greenm01/poly2tri
2.2 布尔运算
文中的方法分为两部分:
- 区分一个点是mesh内部的还是外部的;
- 创建sub-meshes,然后进行merge;
本文中仅对属于相交三角形的点进行了区分。
2.2.1. Point classify
假设mn为(Delta abc)和(Delta def)的交线。这两个三角形分别属于不同的mesh。(n_{abc})和(n_{def})分别是(Delta abc)和(Delta def)的法向量,具体为((x_{n1}, y_{n1}, z_{n1})), ((x_{n2}, y_{n2}, z_{n2}))。(p(x_1,y_1,z_1))和(q(x_2,y_2,z_2))分别是(Delta abc)和(Delta def)的上面的一个点。那么平面方程如下:
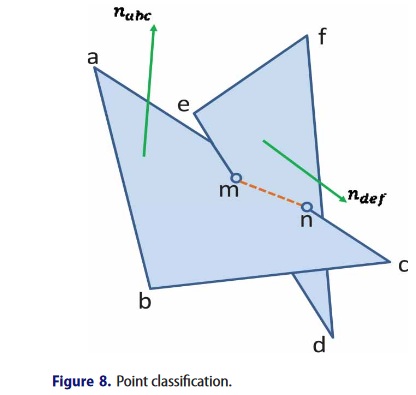
上图中,两个三角形相交于m,n点,对a,c,e,d点的内外位置进行判断。a位于包含(Delta def)的mesh的内部,d位于包含(Delta abc)的mesh的内部。c,e点位于外部。对于退化的相交场景,至少一个三角形的一个点在另一个三角形对应的mesh上。当相交三角形的所有顶点都进行了判断,分别标记了“in”,“out”,“on”,下面就要进行sub-meshes的创建。
2.2.2. create sub-meshes and merging them
不同类型的mesh定义:
- (M_A), (M_B)待处理的两个mesh;
- (M_{AinB}),来自(M_A)位于(M_B)内部的三角形集合;
- (M_{AoutB}),来自(M_A)位于(M_B)外部的三角形集合;
- 同理定义:(M_{BinA}, M_{BoutA});
- (M_{onAB}):同时属于(M_A), (M_B)的网格(共面相交的时候);
那么不同布尔操作的结果如下:
- (M_A cup M_B (union): M_{AoutB} + M_{BoutA} + M_{onAB})
- (M_A cap M_B (intersection): M_{AinB} + M_{BinA} + M_{onAB})
- (M_A - M_B(difference): M_{AoutB} + M_{BinA})
具体伪代码类似如下:

计算过程示意图如下: