离散化

有时候会碰到一些问题给的数不多，但是值很大，比如给五个数，1274,2491294,28742,1882,1，这五个数很分散，在树状数组中，如果用这几个数的值作为下标的话，那就相当浪费了，而且数据要是太大（或者出现负数），下标甚至还会无法储存

这个时候如果我们把这五个数变成2,5,4,3,1，对应他们的相对大小关系，那么问题就好解决多了

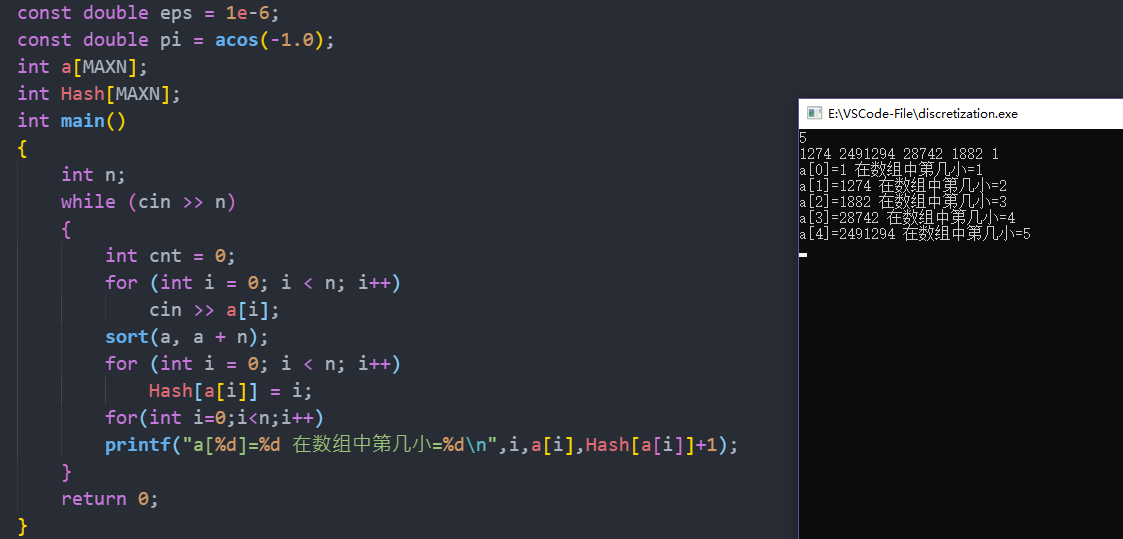
写了个概念性的代码，基本没什么实际用途，毕竟Hash数组的下标存的还是原来的值，就个大概的想法

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define inf 0x3f3f3f3f
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll MAXN = 1e6 + 7;
const ll MAXM = 1e3 + 7;
const ll MOD = 1e9 + 7;
const double eps = 1e-6;
const double pi = acos(-1.0);
int a[MAXN];
int Hash[MAXN];
int main()
{
    int n;
    while (cin >> n)
    {
        int cnt = 0;
        for (int i = 0; i < n; i++)
            cin >> a[i];
        sort(a, a + n);
        for (int i = 0; i < n; i++)
            Hash[a[i]] = i;
        for(int i=0;i<n;i++)
        printf("a[%d]=%d 在数组中第几小=%d
",i,a[i],Hash[a[i]]+1);
    }
    return 0;
}

 

下面是两个比较常用的离散化方法

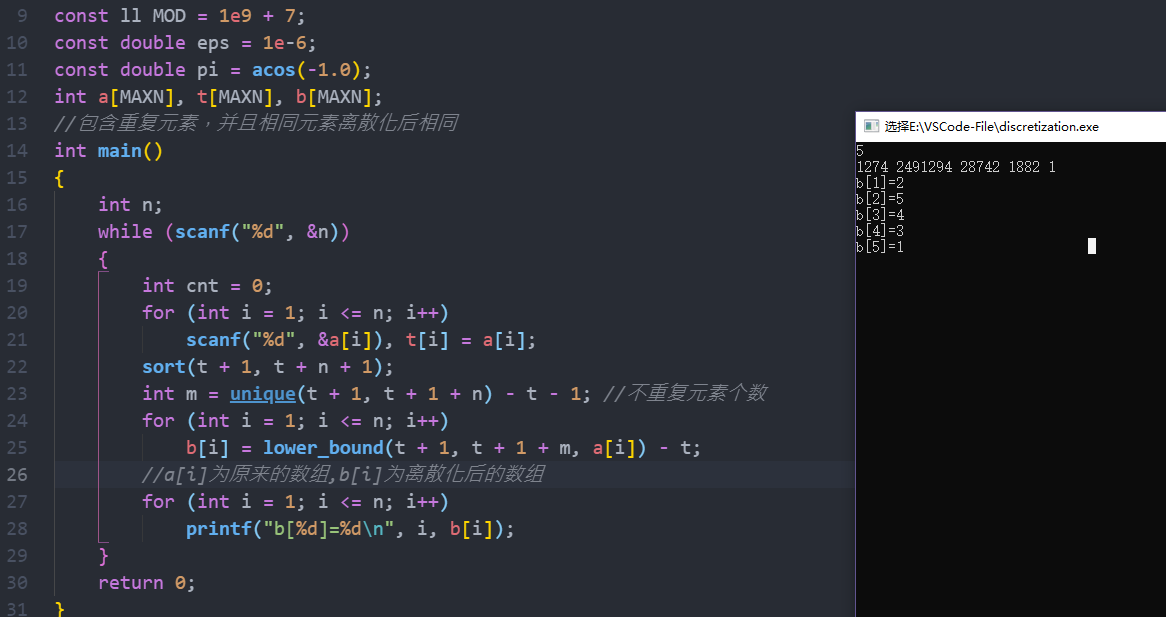
1:包含重复元素，相同元素离散化后也相同,在这种情况下推荐使用

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define inf 0x3f3f3f3f
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll MAXN = 1e5 + 7;
const ll MAXM = 1e3 + 7;
const ll MOD = 1e9 + 7;
const double eps = 1e-6;
const double pi = acos(-1.0);
int a[MAXN], t[MAXN], b[MAXN];
//包含重复元素，并且相同元素离散化后相同
int main()
{
    int n;
    while (scanf("%d", &n))
    {
        int cnt = 0;
        for (int i = 1; i <= n; i++)
            scanf("%d", &a[i]), t[i] = a[i];
        sort(t + 1, t + n + 1);
        int m = unique(t + 1, t + 1 + n) - t - 1; //不重复元素个数
        for (int i = 1; i <= n; i++)
            b[i] = lower_bound(t + 1, t + 1 + m, a[i]) - t;
        //a[i]为原来的数组,b[i]为离散化后的数组
        for (int i = 1; i <= n; i++)
            printf("b[%d]=%d
", i, b[i]);
    }
    return 0;
}

 

有个要注意的地方 1 1 2 2 3 3 4 4 5 7 8 unque后是1 2 3 4 5 7 8 4 5 7 8，只改变了前七个数字，后面的四个数字不变（最好自己写个试试看）

2：复杂度低，1.包含重复元素，并且相同元素离散化后不相同，2.不包含重复元素，并且不同元素离散化后不同，符合这两种的其中一个，推荐使用

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define inf 0x3f3f3f3f
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll MAXN = 1e5 + 7;
const ll MAXM = 1e3 + 7;
const ll MOD = 1e9 + 7;
const double eps = 1e-6;
const double pi = acos(-1.0);
struct Node
{
    int data, id;
    bool operator<(const Node &a) const
    {
        return data < a.data;
    }
};
Node num[MAXN];
int b[MAXN], n;
/* 第二种方式其实就是排序之后，枚举着放回原数组
用一个结构体存下原数和位置，按照原数排序
结构体里面写个重载，也可以写一个比较函数
最后离散化后数在b数组里面*/
int main()
{
    while (~scanf("%d", &n))
    {
        for (int i = 1; i <= n; i++)
        {
            scanf("%d", &num[i].data);
            num[i].id = i;
        }
        sort(num + 1, num + n + 1);
        for (int i = 1; i <= n; i++)
            b[num[i].id] = i;
        for (int i = 1; i <= n; i++)
            printf("b[%d]=%d
", i, b[i]);
    }
    return 0;
}