洛谷P3884 二叉树问题

题目描述

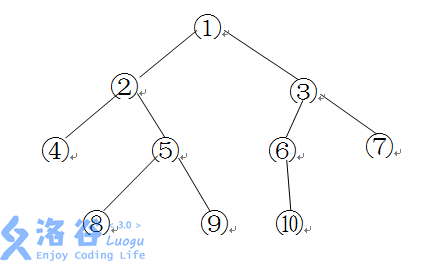
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：(4) 宽度：(4)（同一层最多结点个数）

结点间距离： (⑧→⑥为8 (3×2+2=8))

(⑥→⑦为3 （1×2+1=3）)

注：结点间距离的定义：由结点向根方向（上行方向）时的边数(×2)，

与由根向叶结点方向（下行方向）时的边数之和。

输入输出格式

输入格式：

输入文件第一行为一个整数(n(1≤n≤100))，表示二叉树结点个数。接下来的(n-1)行，表示从结点(x)到结点(y)（约定根结点为(1)），最后一行两个整数(u、v)，表示求从结点(u)到结点(v)的距离。

输出格式：

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点(u)到结点(v)间距离。

输入输出样例

输入样例#1：

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出样例#1：

4
4
8

思路：对于第一个子问题，就是找树上最深的点，一遍(dfs)即可实现，对于第二个子问题，就是看看相同深度的点数目的最大值是多少，对于对三个子问题，就是通过(LCA)求两点间的树上距离。

代码：

#include<cstdio>
#include<algorithm>
#define maxn 107
using namespace std;
int f[maxn][7],n,x,y,js[maxn],maxx,head[maxn],num,d[maxn],zrj;
struct node {
  int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      maxx=max(maxx,d[v]);
      dfs(v,u);
    }
  }
}
inline int lca(int a, int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=6;i>=0;--i) 
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=6;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  scanf("%d",&n);
  for(int i=1,u,v;i<n;++i) {
    scanf("%d%d",&u,&v);
    ct(u,v);ct(v,u);
  }
  dfs(1,0);
  for(int i=1;i<=n;++i) js[d[i]]++;
  for(int i=1;i<=maxx;++i) zrj=max(zrj,js[i]);
  for(int j=1;j<=6;++j)
  for(int i=1;i<=n;++i)
  f[i][j]=f[f[i][j-1]][j-1];
  scanf("%d%d",&x,&y);
  printf("%d
%d
%d
",maxx+1,zrj,(d[x]-d[lca(x,y)])*2-d[lca(x,y)]+d[y]);
  return 0;
}