定义:给定一个有向图,无出边的点的SG值定义为0,其他点的SG值定义为到不了的最小的自然数
具体问题:给定一个石子集合M,再给定一个可以取的数的集合N,求先手必胜还是必败。
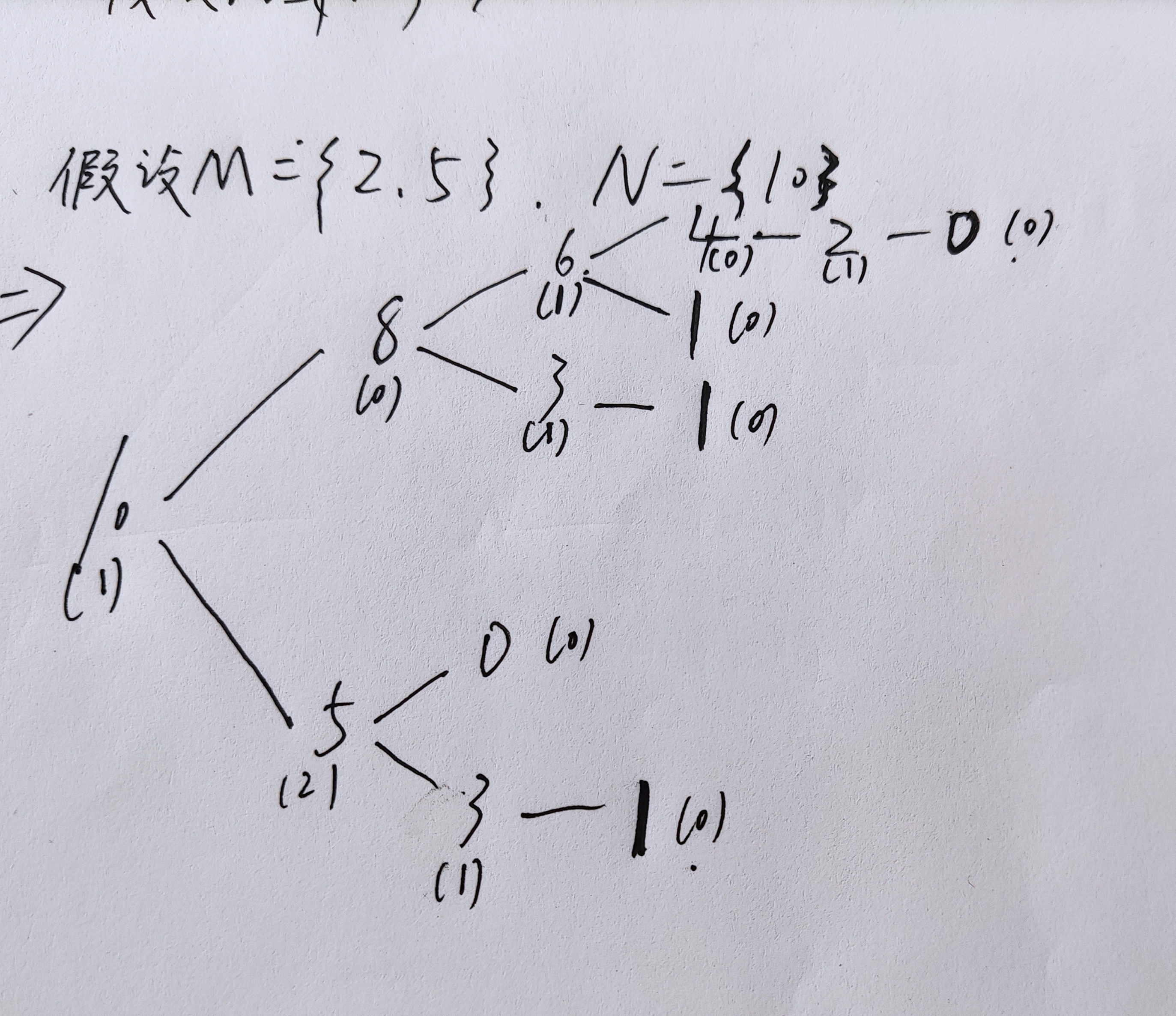
所以SG(10) > 0,所以先手必胜。
证明:
(1)最终失败态为0
(2)非零一定可以变成0
(3)0一定不能走到0
由SG函数定义可知上述性质皆正确,所以SG(x)>0,则意味着先手必胜
那么如果有多堆石子怎么办呢?
可以发现,这个和Nim游戏简直太像了。
在集合游戏中SG(x)=k,代表它可以走向{0,1...k-1}中的和状态
再Nim游戏中,一堆石子x也是可以可以走向小于x的任何状态的
所以解决方法也是类似的,直接将每个集合的SG函数异或起来,异或值等于res,如果大于0则是先手必胜,否则先手必败。
证明:
需要证明(1)终点态res=0
(2)非零态必然可以转移到0态
(3)0态不可能转移到0态

1 #include<algorithm> 2 #include<cstring> 3 #include<unordered_set> 4 #include<iostream> 5 using namespace std; 6 int n,m; 7 const int N=110,M=10010; 8 int s[N],f[M]; 9 int sg(int x){ 10 if(f[x]!=-1){ 11 return f[x]; 12 } 13 unordered_set<int> se; 14 for(int i=0;i<m;i++){ 15 int sum=s[i]; 16 if(x>=sum) 17 se.insert(sg(x-sum)); 18 } 19 for(int i=0;;i++){ 20 if(!se.count(i)){ 21 return f[x]=i; 22 } 23 } 24 } 25 int main(void){ 26 cin>>m; 27 for(int i=0;i<m;i++) cin>>s[i]; 28 memset(f,-1,sizeof(f)); 29 int res=0; 30 cin>>n; 31 for(int i=0;i<n;i++){ 32 int t; 33 cin>>t; 34 res^=sg(t); 35 } 36 if(res){ 37 puts("Yes"); 38 }else{ 39 puts("No"); 40 } 41 return 0; 42 }
拆分Nim游戏
题目:https://www.acwing.com/problem/content/896/
游戏一定可以终止,因为最大值一直在减小。(严格证明可用数学归纳法--证明n的两个子状态可以终止即可)
终止态为全零。
定义 SG(终止)= 0
所以res=SG(a1)^SG(a2)^...^SG(an)
若res==0,则先手必败,否则先手必胜。
而SG(n)=mex(SG(i)^SG(j)) (i<x&&j<=i) ,必须j<=i,因为x=1时SG(x)!= 0
1 #include<unordered_set> 2 #include<cstring> 3 #include<iostream> 4 using namespace std; 5 const int N=110; 6 int f[N]; 7 int sg(int x){ 8 if(f[x]!=-1) return f[x]; 9 unordered_set<int> S; 10 for(int i=0;i<x;i++){ 11 for(int j=0;j<=i;j++){ 12 S.insert(sg(i)^sg(j)); 13 } 14 } 15 for(int i=0;;i++){ 16 if(!S.count(i)){ 17 return f[x]=i; 18 } 19 } 20 } 21 int main(void){ 22 memset(f,-1,sizeof(f)); 23 int n; 24 cin>>n; 25 int res=0; 26 for(int i=0;i<n;i++){ 27 int x; 28 cin>>x; 29 res^=sg(x); 30 } 31 if(res) puts("Yes"); 32 else puts("No"); 33 return 0; 34 }