动态规划--线性DP-1

线性DP：在线性空间上进行答案的递推。

1、数字三角形问题

https://www.acwing.com/problem/content/900/

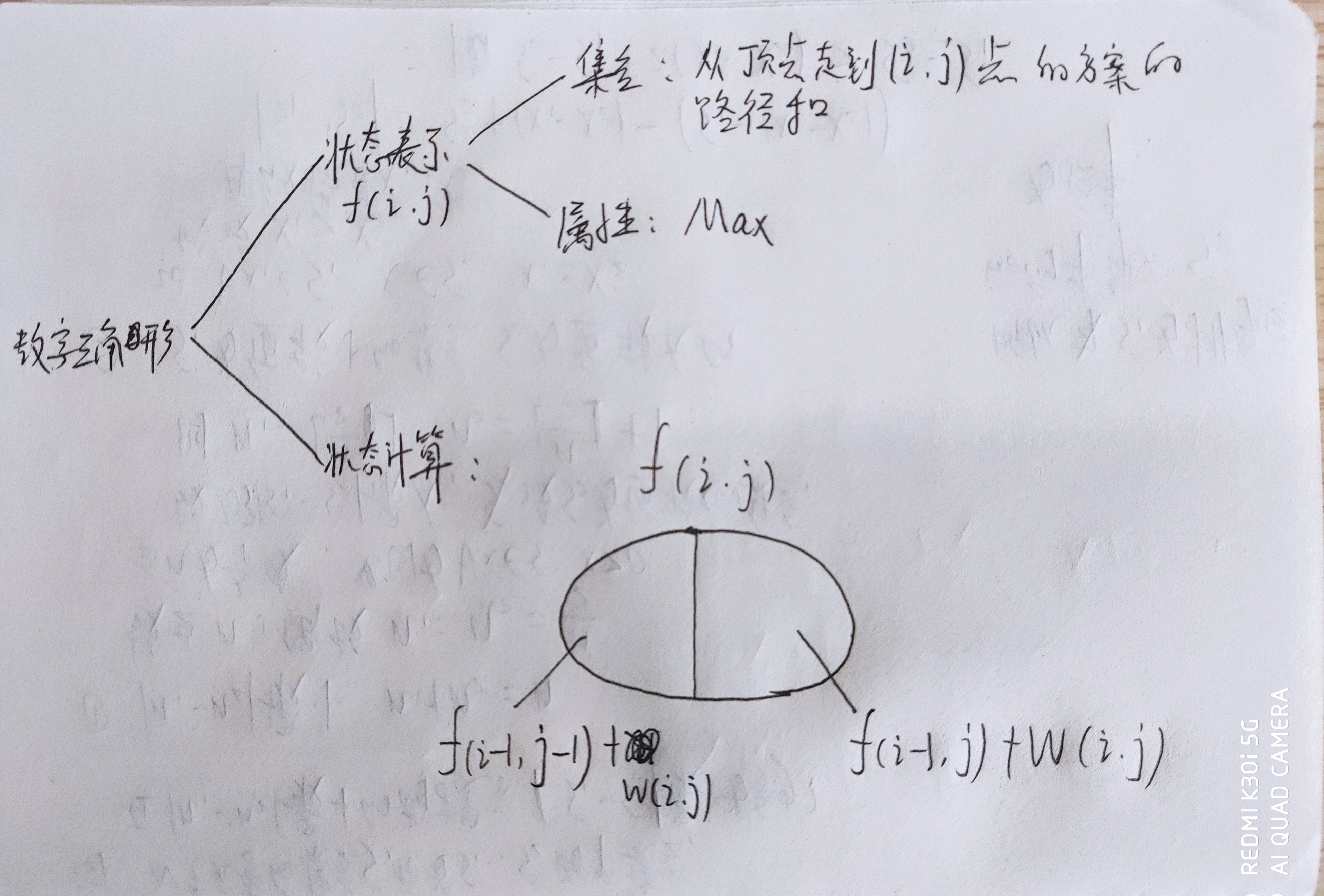
#include<iostream>
#include<cstring>
using namespace std;
const int N=510;
int w[N][N],f[N][N];
int main(void){
    memset(f,0xa0,sizeof f);//初始化为无穷小
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>w[i][j];
        }
    }
    f[1][1]=w[1][1];//第一层得初始化
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            f[i][j]=max(f[i-1][j-1]+w[i][j],f[i-1][j]+w[i][j]);
        }
    }
    int res=-99999;
    for(int i=1;i<=n;i++){
        res=max(res,f[n][i]);
    }
    cout<<res;
    return 0;
}

2、最长上升子序列问题

https://www.acwing.com/problem/content/897/

#include<iostream>
using namespace std;
const int N=1010;
int w[N],f[N];
int main(void){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>w[i];
    }
    
    f[1]=1;
    for(int i=2;i<=n;i++){
        f[i]=1;
        for(int j=1;j<i;j++){
            if(w[j]<w[i]){
                f[i]=max(f[j]+1,f[i]);
            }
        }
    }
    
    int res=0;
    for(int i=1;i<=n;i++){
        res=max(res,f[i]);
    }
    cout<<res;
    return 0;
}

3、最长上升子序列问题优化

https://www.acwing.com/problem/content/898/

 

那么我们就可以通过二分找到对于每一个数，他的最长的上升子序列长度是多少。

因为我们只需要二分找到不大于a[ i ] 的最大的f [ j ] ，j+1就是以a[ i ] 结尾的最长上升子序列的长度。

#include<iostream>
using namespace std;
const int N=100010;
int a[N],f[N];
int main(void){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    int len=0;
    f[0]=-2e9;//设置初始状态，长度为0的结尾为-INF
    for(int i=0;i<n;i++){
        int l=0,r=len;
        while(l<r){
            int mid=(l+r+1)>>1;
            if(a[i]<=f[mid]){
                r=mid-1;
            }else{
                l=mid;
            }
        }
        len=max(len,r+1);
        f[r+1]=a[i];
    }
    cout<<len;
    return 0;
}