开新坑辣。。。。。
排列组合
排列:P(n,r) = n! / (n-r)!
组合:C(n,r) = n! / r!(n-r)!
圆排列:P(n,r) / r
多重集排列:
- 令S是一个多重集,它有k个不同类型的元素,每一个元素都有无穷重复个数。那么S的r-排列的个数为k^r。
- 令S是一个多重集,它有k个不同类型的元素,各元素重数为n1,n2,...,nk。设S的大小为n = n1 + n2 + ... + nk。则排列数等于n! / (n1!n2!...nk!)
抽屉原理(鸽巢原理)
wiki百科介绍
理解起来还是比较容易的,拓展有拉姆齐定理(虽然是图论上的内容)
特殊序列
掌握它们的应用和推导方式
Catalan序列
wiki百科介绍
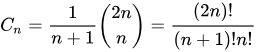
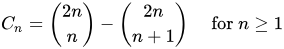
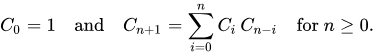
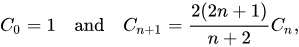
前20项为(OEIS中的数列A000108):1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190
Stiring数
wiki百科介绍
第一类:将p个有区别的球排成k个非空的圆排列的方案数
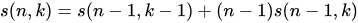
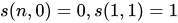

第二类:将p个有区别的球放到k个相同盒子中,奥球没有空盒的方案数
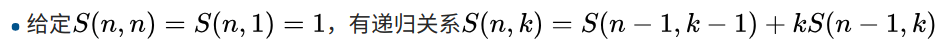

两者关系: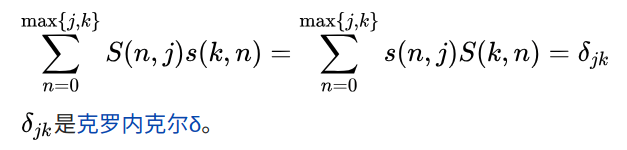
容斥原理

错位排列
公式法:
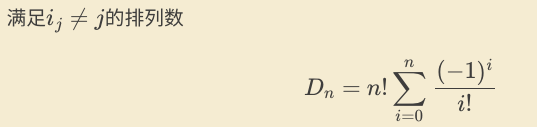
递推法:
考察n≥3时的错位排列,把数字n单独拿出来看,先把n放在第n位。设P是{1,2,...,n-1}的一个排列
- 如果P是一个错位排列,把其中任意一个数与n交换仍然是一个错位排列,这样的情形可以得到(n-1)D_n-1个{1,2,...,n}的错位排列
- 如果P不是错位排列,并且只存在一个位置不符合要求(P_x = x)将x和n交换后又是一个错位排列。这里可以得到(n-1)D_n-2个{1,2,...,n}的错位排列。
- 其他情形都不能得到错位排列
D_n = (n-1)(D_n-1 + D_n-2) (D1 = 0, D2 = 1)
Mobius反演
NULL
棋盘多项式
母函数(生成函数)
普通型生成函数讲解
在学习FFT的时候,已经知道可以用卷积来计算生成函数计数问题,它可以针对一般的多项式计算乘积,而在整数拆分这个问题里,有n个表达式,需要做n次卷积,复杂度O(n²logn),但FFT常数是很大的,观察得知每个多项式是很有规律的,它的第i个多项式中系数为1的项都间隔了i-1个系数为0项,所以我们可以用一个每次变化i-1的k循环来遍历得到每层卷积后的多项式
指数型生成函数讲解
Polya计数定理
置换群
- 首先给你一个序列,假如: s = {1 2 3 4 5 6}
然后给你一个变换规则 t = {6 3 4 2 1 5}
就是每一次按照t规则变换下去
第一次:6 3 4 2 1 5
第二次:5 4 2 3 6 1
第三次:1 2 3 4 5 6
发现经过几次会变换回去,再变换下去就是循环的了,这就是一个置换群
我们可以这样表示一个置换群,比如按照上面变化规则
1->6->5->1 这些是一个轮换
2->3->4->2 这些是一个轮换
所以可以写为 t = { {1 6 5},{ 2 3 4 } } - 如果一个状态经过置换f后跟原来相同,
即S[1]=S[a1],S[2]=S[a2],…,S[n]=S[an]
则称该状态为f 的不动点。 - 题目中常常出现“本质不同的方案数”,一般是指等价类的数目,题目定义一个等价关系,满足等价关系的元素属于同一等价类。等价关系通常是一个置换集合F,如果一个置换能把其中一个方案映射到另一个方案,则二者是等价的。
那么,置换构成的群就是置换群,就是交换排列顺序而已
二面体群
wiki百科介绍
翻转本质上也是一种置换规则

Burnside引理
设G是集合X上的一个置换群(可以理解为合理的所有的置换方案的集合),S(g)为C中的不动点的着色集合,则可以证明等价类数目为所有S(g)的平均值。
- 一正方形分成4格,2着色,有多少种方案?其中,经过转动相同的图象算同一方案
对于每种格子我们都有两种选择,所以会有一下16种方案
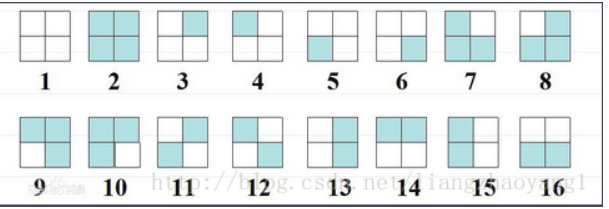
- 不动:所有的情况都是不动点 16
- 旋转90° (1)(2)是不动点 2
- 旋转180° (1)(2)(11)(12)是不动点 4
- 旋转270° (1)(2)是不动点 2
(16+2+4+2)/4=6种
Polya计数定理
先把所有方案重复计算相同的次数,再把结果除以重复的次数
设G是集合x上的一个置换群,X中每个元素可以被染成k种颜色,则不等价的着色数为:P=(1 / |G|) *∑K^(nc(g)),nc(g) 为置换中循环节的个数