数据结构6.6_赫夫曼树及其应用

赫夫曼树：http://data.biancheng.net/view/33.html

赫夫曼树的原理和构建：https://www.cnblogs.com/enumhack/p/7473043.html 

赫夫曼树又称为最优树，是一类带权路径长度最短的树。

最优二叉树（赫夫曼树）：

路径：一个树结点到另一个结点之间的分支构成了路径。

路径长度：分支的数目。

树的路径长度：从树根到每一结点的路径长度之和。

树的带权路径长度：树的所有叶子结点的带权路径长度之和。通常记作WPL

结点的带权路径长度：该结点到树根之间的路径长度与结点上的权的乘积。

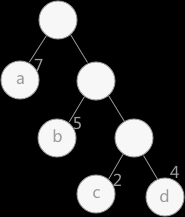
这个数的带权路径长度：WPL=7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

假设有n个权值{w1, w2, w3, ...,wn}，构造一棵有n个叶子结点的二叉树，每个叶子结点带权为wi。

其中带权路径长度WPL最小的二叉树称做 最优二叉树 或 赫夫曼树。

如何构造赫夫曼树？

赫夫曼给出一个带有一般规律的算法，俗称赫夫曼算法。 

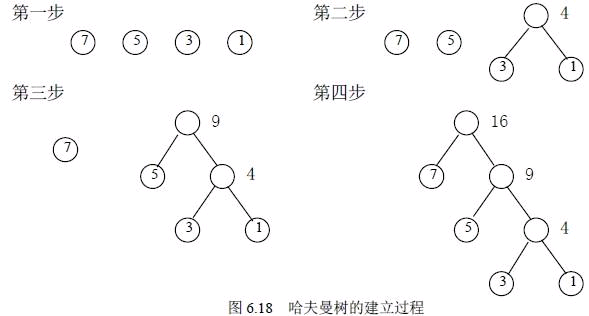
构造方法：

    给定N个权值分别为w1, w2, ..., Wn的节点。构造赫夫曼树的算法描述如下：

    1）将这N个结点分别作为N棵树仅含一个结点的二叉树，构成森林F.

    2）构造一个新节点，并从F中选取两棵根结点权值最小的树作为新节点的左、右子树，并且将新节点的权值置为左、右子树上根结点的权值之和。

    3）从F中删除刚才选出的两棵树，同时将新得到的树加入F中。

    4）重复步骤2和3，直至F中只剩下一棵树为止。

 

赫夫曼编码

赫夫曼编码是一种被广泛应用而且非常有效的数据压缩编码，它是可变长度编码。可变长编码即可以对待处理字符串中不同字符使用不等长的二进制位表示，可变长编码比固定长度编码好很多，可以对频率高的字符赋予短编码，而对频率较低的字符则赋予较长一些的编码，从而可以使平均编码长度减短，起到压缩数据的效果。

       赫夫曼编码是前缀编码。如果没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码。对前缀编码的解码也是相对简单的，因为没有一个码是另一个编码的前缀，所以可以识别出第一个

编码，将它翻译为原码，再对余下的编码文件重复同样操作。

        赫夫曼编码首先要构造一棵赫夫曼树，首先，将每个出现的字符当做一个独立的结点，其权值作为它出现的频度（或次数），然后构造哈夫曼树。显然所有字符节点均出现在叶子结点中。我们可以将字符的编码解释为从根至该字符路径上标记的序列，其中标记为0表示"转向左孩子"，标记为1表示为"转向右孩子"。 如下图，矩形方块表示字符及出现的次数

 

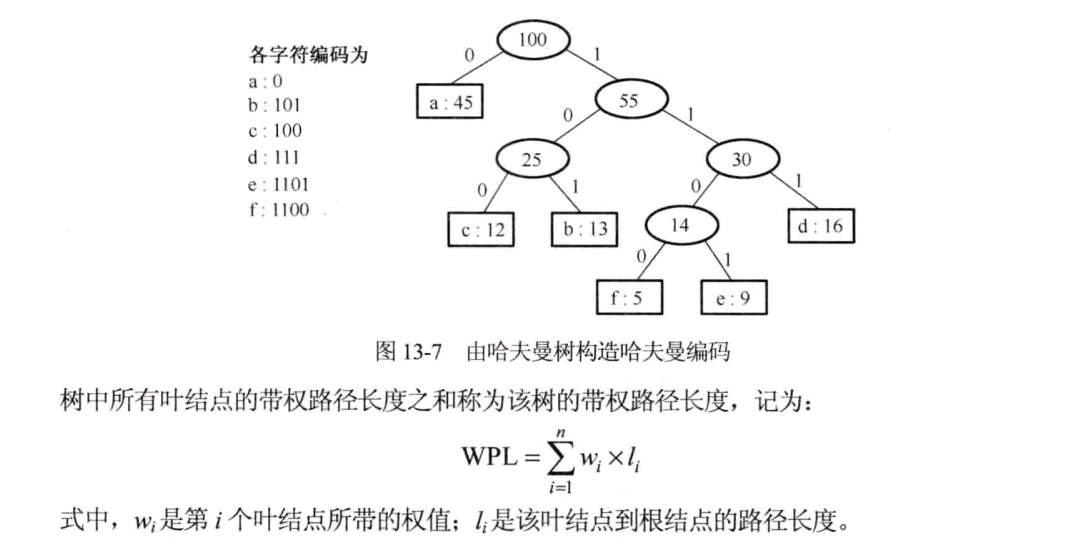
赫夫曼编码就是让那些高频使用的词汇用更短的编码来实现，以达到根据使用频率来有效压缩数据的目的，这样的编码更高效。

赫夫曼编码是前缀编码。即没有一个编码是另一个编码的前缀。

赫夫曼编码的存储表示及赫夫曼算法：

typedef struct {
    unsigned int weight;
    unsigned int parent, lchild, rchild;
}HTNode, *HuffmanTree;        //动态分配数组存储赫夫曼树

typedef char * *HuffmanCode;  //动态分配数组存储赫夫曼编码表

//赫夫曼算法
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC,int * w, int n)
{
    //w表示n个字符的权值（w>0），n表示赫夫曼树有多少个字符（叶子节点）
    if(n<=1) return;
    m = 2*n - 1;  //赫夫曼树的节点总数
    HT = (HuffmanTree)malloc((m+1)*sizeof(HTNode));//为赫夫曼树分配空间,0号单元未用；
    //两个for循环对节点进行初始化；
    for(p=HT, i=1; i<=n; ++i, ++p, ++w)
    {
        *p = {*w, 0, 0, 0};
    }
    for(;i<=m;++i, ++p)
    {
        *p = {0, 0, 0, 0};
    }
    //构建赫夫曼树
    for(i = n+1; i<=m; ++i)
    {
        //在HT[1 .. i-1]选择parent为0且weight最小的两个结点，其序号分别为s1和s2
        Select(HT, i-1, s1, s2);
        HT[s1].parent = i;
        HT[s2].parent = i;
        HT[i].lchild = s1;
        HT[i].rchild = s2;
        HT[i].weight = HT[s1].weight+HT[s2].weight;     
    }

    HF = (HuffmanCode)malloc((n+1)*sizeof(char *));//分配字符编码的头指针向量
    cd = (char *)malloc(n * sizeof(char));  //分配求编码的临时工作空间
    cd[n-1] = '';  
    for(i=1; i<=n; ++i)  //逐个字符求赫夫曼编码
    {
        start = n-1;
        for(c = i, f = HT[i].parent; f !=0; c=f, f=HT[f].parent)
            if(HT[f].lchild == c)   cd[- - start]="0";
            else  cd[- - start] = "1";
        HC[i]= (char *)malloc((n-start)*sizeof(char));
        strcpy(HC[i], &cd[start]);
    }
    free(cd);
}//HufmanCoding

这个赫夫曼算法由HuffmanCoding()函数实现；

我们要对n个字符编码；

例如A B C D，编码成相应的赫夫曼编码；但是要提供这四个字符的权重。

函数的参数介绍：

HuffmanTree &HT    //给定一个赫夫曼树的结点

HuffmanCode &HC  //输出的赫夫曼编码数组，字符数组

int * w    //表示n个字符的权重，用int数组

int n      //表示有n个字符

函数的工作内容：

1、 进行分配足够多的结点，并进行结点初始化；

2、将结点构成赫夫曼树；

3、进行赫夫曼编码；

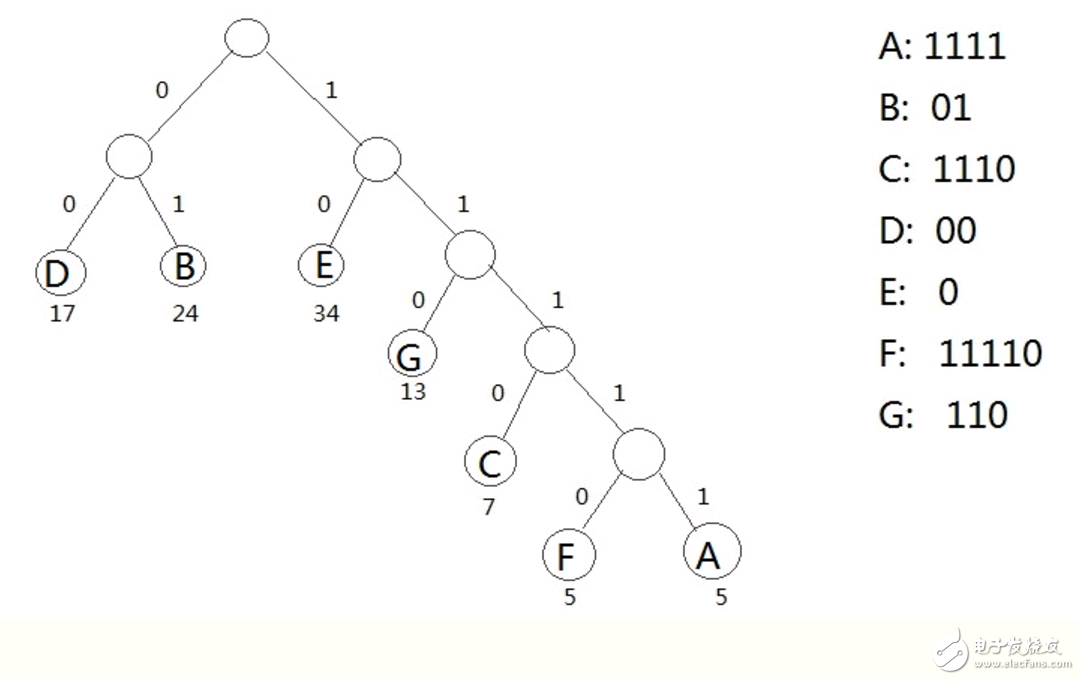
结合下面的图理解39行到47行代码：即赫夫曼编码的过程

例如：C字符要编码成1110。 

先给赫夫曼编码的每个数字编个号：c1=1，c2=1，c3=1, c4 =0;

赫夫曼算法的原理是会对字符进行从叶子节点到根的方式逆向求编码；

求c4 ：这里会看到C结点属于其父节点CF1的左孩子，所以可知c4=0；然后看到CF1还有父结点，继续向上走；

//当然逆向求得时候是不知道自己最终编码成几个数字的，终止条件就是遍历到根为止。也就是说这里c4是为了说明方便，一开始是不知道c几的。

求c3：然后看CF1结点是其父节点CF2的右孩子，所以可知c3=1; 然后看到CF2还有父结点，继续向上走；

求c2：然后看到CF2结点是其父节点CF3的右孩子，所以可知c2=1; 然后看到CF2还有父结点，继续向上走；

求c1：然后看到CF3结点是其父节点CF4的右孩子，所以可知c1=1;  这时候CF4没有父结点了，终止向上遍历；

就这样通过遍历赫夫曼树的方式对字符的实现了赫夫曼编码。