参考链接:
回溯法(八皇后问题):http://data.biancheng.net/view/34.html
详细讲解回溯算法:https://blog.csdn.net/gardenpalace/article/details/84625537
回溯算法超通俗易懂详尽分析:https://blog.csdn.net/sinat_27908213/article/details/80599460
回溯算法(BackTracking)
在程序设计中,由相当一类求一组解、或求全部解或求最优解的问题,不是根据某种确定的计算法则,而是利用试探和回溯的搜索技术求解。
回溯法时设计递归过程中的一种方法。
这个求解过程实质上是一个先序遍历一棵“状态树”的过程。只是这棵树不是遍历前预先建立的,而是隐含在遍历过程中。
回溯算法实际上一个类似枚举的深度优先搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回(也就是递归返回),尝试别的路径。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
回溯法说白了就是穷举法。回溯法一般用递归来解决。
回溯法的求解过程实际上是一个先序遍历一棵“状态树”的过程,只是这棵树不是预先建立的,而是隐含在遍历过程中。
一个复杂问题的解决方案是由若干个小的决策步骤组成的决策序列,所以一个问题的解可以表示成解向量X=(x1,x2,.....xn),
其中分量xi对应第i步的选择,X中个分量xi所有取值的组合构成问题的解向量空间,简称解空间或者解空间树(因为解空间一般用树形式来组织),
由于一个解向量往往对应问题的某个状态,所以解空间又称为问题的状态空间树。
按照DFS算法的策略,从跟结点出发搜索解空间树。首先根结点成为活结点(指自身已生成但其孩子结点没有全部生成的结点),同时也成为当前的扩展结点(指正在产生孩子结点的结点,也称为E结点)。
在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为新的活结点,并成为当前扩展结点。
如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成了死结点(指其所有子结点均已产生的结点)。
此时应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。
回溯法以这种方式递归地在解空间中搜索,直到找到所要求的解或解空间中已无活结点为止。
所以回溯法体现出走不通就退回再走的思路。
练习题1:求含n个元素的集合的幂集
参考链接:https://blog.csdn.net/summer_dew/article/details/83921730
A={1,2,3}
ρ(A) = { {1,2,3}, {1,2}, {1,3}, {1}, {2,3}, {2}, {3}, ∅ }
集合A的幂集是由集合A的所有子集所组成的集合。
幂集中的每个元素是一个集合。
从幂集中的每个元素的角度来看:或是空集,或者包含集合A中一个元素,或者包含集合A中两个元素,或者包含集合A中三个元素,或者等于集合A。
从集合A的角度来看:它其中的元素只有两种状态。要么属于幂集的元素集 ,要么不属于幂集元素集。
求幂集ρ(A) 的元素的过程可以看成是依次对集合A中元素进行“取”或“舍”的过程,并且可以用下图所示的二叉树表示:

1 void PowerSet(int i,int n) { 2 // 求含n个元素的集合A的幂集ρ(A)。进入函数时已对A中前i-1个元素坐了取舍处理 3 // 现从第i个元素起进行取舍处理。若i>n,则求得幂集的一个元素,并输出之 4 // 初始调用:PowerSet(1,n); 5 if (i>n) 输出幂集的一个元素 6 else { 7 取第i个元素;PowerSet(i+1, n); 8 舍第i个元素;PowerSet(i+1, n); 9 } 10 }
接下来假设以线性表来表示集合A,则算法的具体表示如下:
1 void GetPowerSet(int i, List A, List &B) 2 { 3 //线性表A表示集合A,线性表B表示幂集的一个元素; 4 if(i>ListLength(A)) Output(B); 5 else{ 6 GetElem(A,i,x); 7 k = ListLength(B); //k表示进入函数时,ListB的长度,第一次调用本函数时,k=1 8 ListInsert(B,k+1,x); 9 GetPowerSet(i+1,A,B); 10 ListDelete(B,k+1,x); 11 GetPowerSet(i+1,A,B); 12 } 13 }
图中状态变化树是一棵满二叉树:树中每个叶子结点的状态都是求解过程中可能出现的状态(即问题的解)。
【然而】很多问题用回溯和试探求解时,描述求解过程的状态树不是一棵满的多叉树
【非满多叉树】不是满的多叉树:当试探过程中出现的状态和问题所求解产生矛盾时,不再继续试探下去,这时出现的叶子结点不是问题的解的终结状态
此类问题的求解过程可看成是在约束条件下进行先序(根)遍历,并在遍历过程中剪去那些不满足条件的分支
例如,下面的四皇后问题
练习题2: 4皇后问题
参考链接:https://segmentfault.com/a/1190000003733325
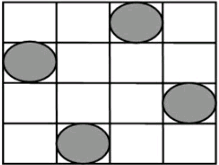
以4皇后为例,其他的N皇后问题以此类推。所谓4皇后问题就是求解如何在4×4的棋盘上无冲突的摆放4个皇后棋子。在国际象棋中,皇后的移动方式为横竖交叉的,因此在任意一个皇后所在位置的水平、竖直、以及45度斜线上都不能出现皇后的棋子:
其实在解决四皇后问题的时候,并不一定要真的构建出这样的一棵解空间树,它完全可以通过一个递归回溯来模拟。所谓的解空间树只是一个逻辑上的抽象。当然也可以用树结构来真实的创建出一棵解空间树,不过那样会比较浪费空间资源,也没有那个必要。
1 #include<stdio.h> 2 3 int count = 0; 4 int isCorrect(int i, int j, int (*Q)[4]) //用于判断当前布局是否合法 5 { 6 int s, t; 7 for(s=i,t=0; t<4; t++) 8 if(Q[s][t]==1 && t!=j) 9 return 0;//判断行 10 for(t=j,s=0; s<4; s++) 11 if(Q[s][t]==1 && s!=i) 12 return 0;//判断列 13 for(s=i-1,t=j-1; s>=0&&t>=0; s--,t--) 14 if(Q[s][t]==1) 15 return 0;//判断左上方 16 for(s=i+1,t=j+1; s<4&&t<4;s++,t++) 17 if(Q[s][t]==1) 18 return 0;//判断右下方 19 for(s=i-1,t=j+1; s>=0&&t<4; s--,t++) 20 if(Q[s][t]==1) 21 return 0;//判断右上方 22 for(s=i+1,t=j-1; s<4&&t>=0; s++,t--) 23 if(Q[s][t]==1) 24 return 0;//判断左下方 25 26 return 1;//否则返回 27 } 28 29 void Queue(int j, int (*Q)[4]) //递归函数,实现回溯遍历 30 { 31 int i,k; 32 if(j==4){//递归结束条件 33 for(i=0; i<4; i++){ 34 //得到一个解,在屏幕上显示 35 for(k=0; k<4; k++) 36 printf("%d ", Q[i][k]); 37 printf(" "); 38 } 39 printf(" "); 40 count++; 41 return ; 42 } 43 for(i=0; i<4; i++){ 44 if(isCorrect(i, j, Q)){//如果Q[i][j]可以放置皇后 45 Q[i][j]=1;//放置皇后 46 Queue(j+1, Q);//递归深度优先搜索解空间树 47 Q[i][j]=0;//这句代码就是实现回溯到上一层 48 } 49 } 50 } 51 52 int main() 53 { 54 int Q[4][4]; 55 int i, j; 56 for(i=0; i<4; i++) 57 for(j=0; j<4; j++) 58 Q[i][j] = 0; 59 Queue(0, Q); 60 printf("The number of the answers are %d ", count); 61 return 0; 62 }