项目:趣味自然数
水仙花数
水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number),水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身。
符合这样规律的数在3位被成为水仙花数,在4位被称作四叶玫瑰数,以及五位的五角星数和六位的六合数和七位的北斗七星数。
不管位数如何变换,但是水仙花数的思想是一样的。
在这里就展示了三位的水仙花数。
public class Narcissistic_number {
public static void main(String[] args) {
for(int i = 100; i < 1000; i++){
int first = i/100;
int second = i/10%10;
int third = i%10;
if((java.lang.Math.pow(first, 3)+java.lang.Math.pow(second, 3)+java.lang.Math.pow(third, 3))==i){
System.out.println("水仙花数为:"+i);
}
}
}
}

我在这里用的是java.lang.Math包中的pow函数。
pow(a,b)表示a的b次方。
完全数
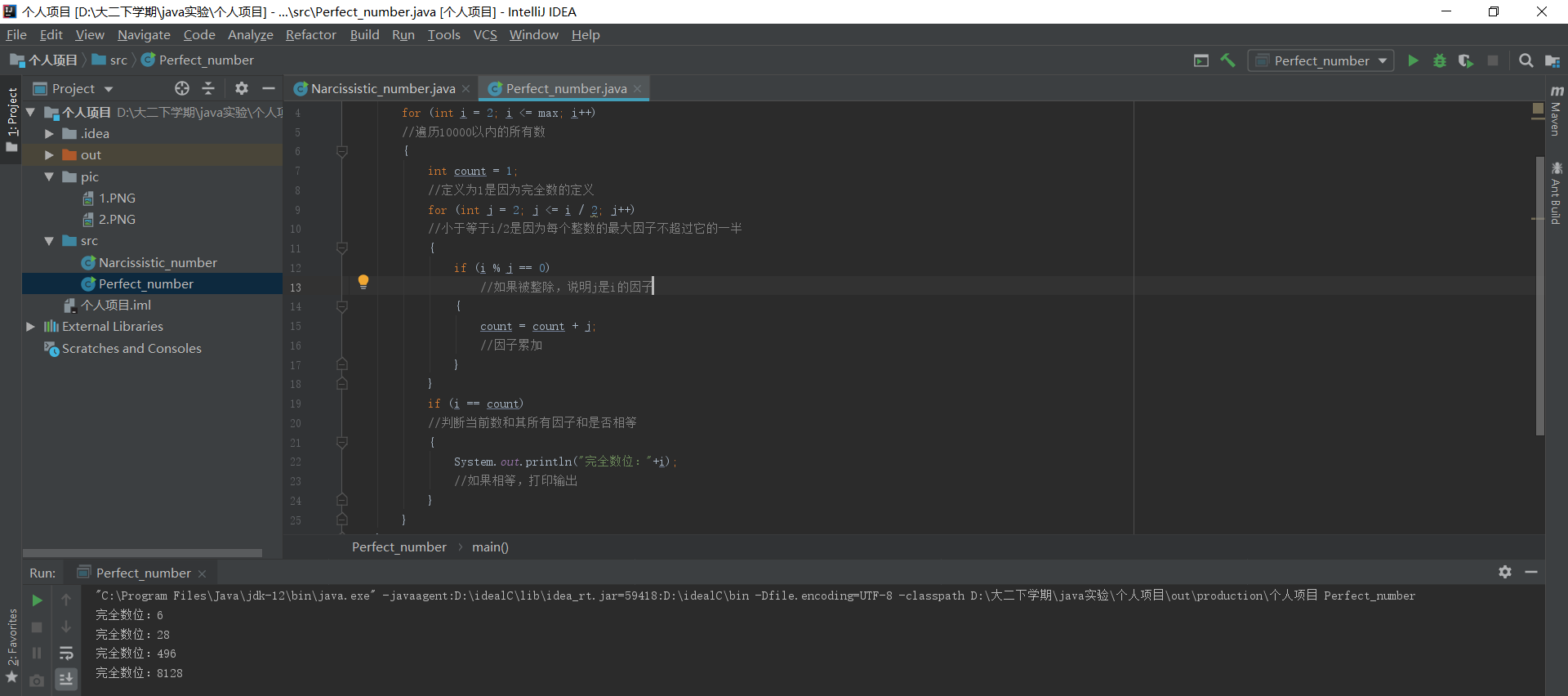
完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。如果一个数恰好等于它的因子之和,则称该数为“完全数”。
完全数的核心便是寻找一个数的真因子,我打算寻找10000以内的完全数,所以我们用试除法就可以寻找到这个数的真因子。在进一步的设计中,我打算用两层循环来完成,第一层循环是用来循环10000以内的数字,第二层循环是用来寻找这个数的真因子,循环次数在根号i之能。
public class Perfect_number {
public static void main(String[] args) {
int max = 10000;
for (int i = 2; i <= max; i++)
//遍历10000以内的所有数
{
int count = 1;
//定义为1是因为完全数的定义
for (int j = 2; j <= Math.sqrt(i); j++)
//小于等于根号i是因为每个整数的最大因子不超过它的根号
{
if (i % j == 0)
//如果被整除,说明j是i的因子
{
count = count + j;
//因子累加
}
}
if (i == count)
//判断当前数和其所有因子和是否相等
{
System.out.println("完全数位:"+i);
//如果相等,打印输出
}
}
}
}
亲密数
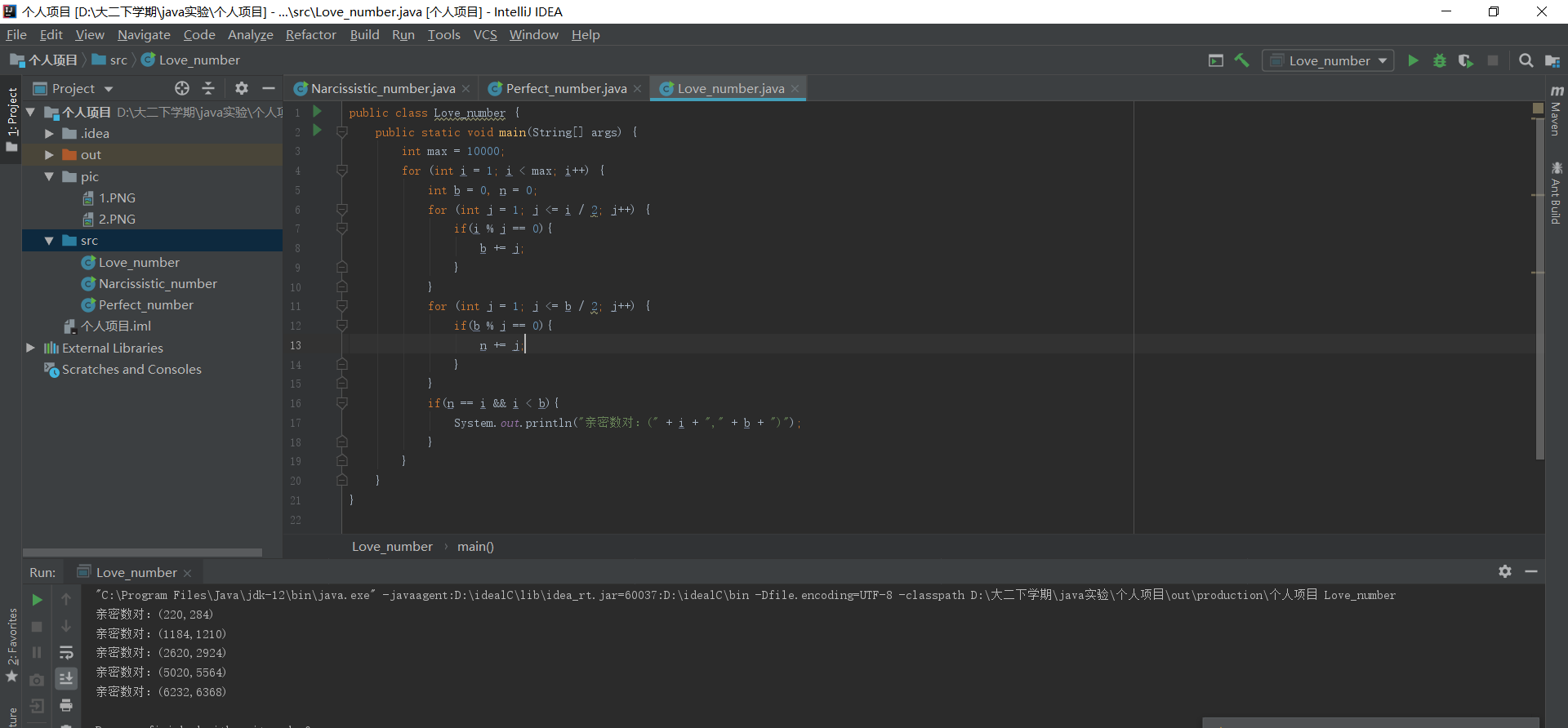
如果a的所有正因子和等于b,b的所有正因子和等于a,因子包括1但不包括本身,且a不等于b,则称a,b为亲密数对。
public class Love_number {
public static void main(String[] args) {
int max = 10000;
for (int i = 1; i < max; i++) {
int b = 0, n = 0;
for (int j = 1; j <= i / 2; j++) {
if(i % j == 0){
b += j;
}
}
for (int j = 1; j <= b / 2; j++) {
if(b % j == 0){
n += j;
}
}
if(n == i && i < b){
System.out.println("亲密数对:(" + i + "," + b + ")");
}
}
}
}
程序设计的时候,并没有想到更好的方法来简化运算,所以只能有两个循环来寻找亲密数对,也就是外循环中,先计算这个数的因子和即可能是亲密数。再计算这个可能是亲密数的因子和,如果两个因子和相等,即这个数是一对亲密数对。
回文数
设n是一任意自然数。若将n的各位数字反向排列所得自然数n1与n相等,则称n为一回文数。
例如,若n=1234321,则称n为一回文数;但若n=1234567,则n不是回文数。
public class palindrome_number {
public static void main(String[] args) {
for (int i = 10; i < 10000; i++) {
if (judge(i)) {
System.out.println(i);
}
}
}
private static boolean judge(int a) {
String s = String.valueOf(a);
int length = s.length();
int j = 0;
while (j <= (length / 2) - 1 && s.charAt(j) == s.charAt(length - j - 1)){
j++;
}
if (j == length / 2) {
return true;
} else {
return false;
}
}
}

回文数的程序设计的思想就是通过利用字符串对应位置进行比较。
String.valueOf(int a)将传入的int类型的a数值转换位一个字符串。
charAt(int i)方法用于返回指定索引处的字符。索引范围为从 0 到 length() - 1。
通过这两个方法来实现了回文数的判断。
勾股数
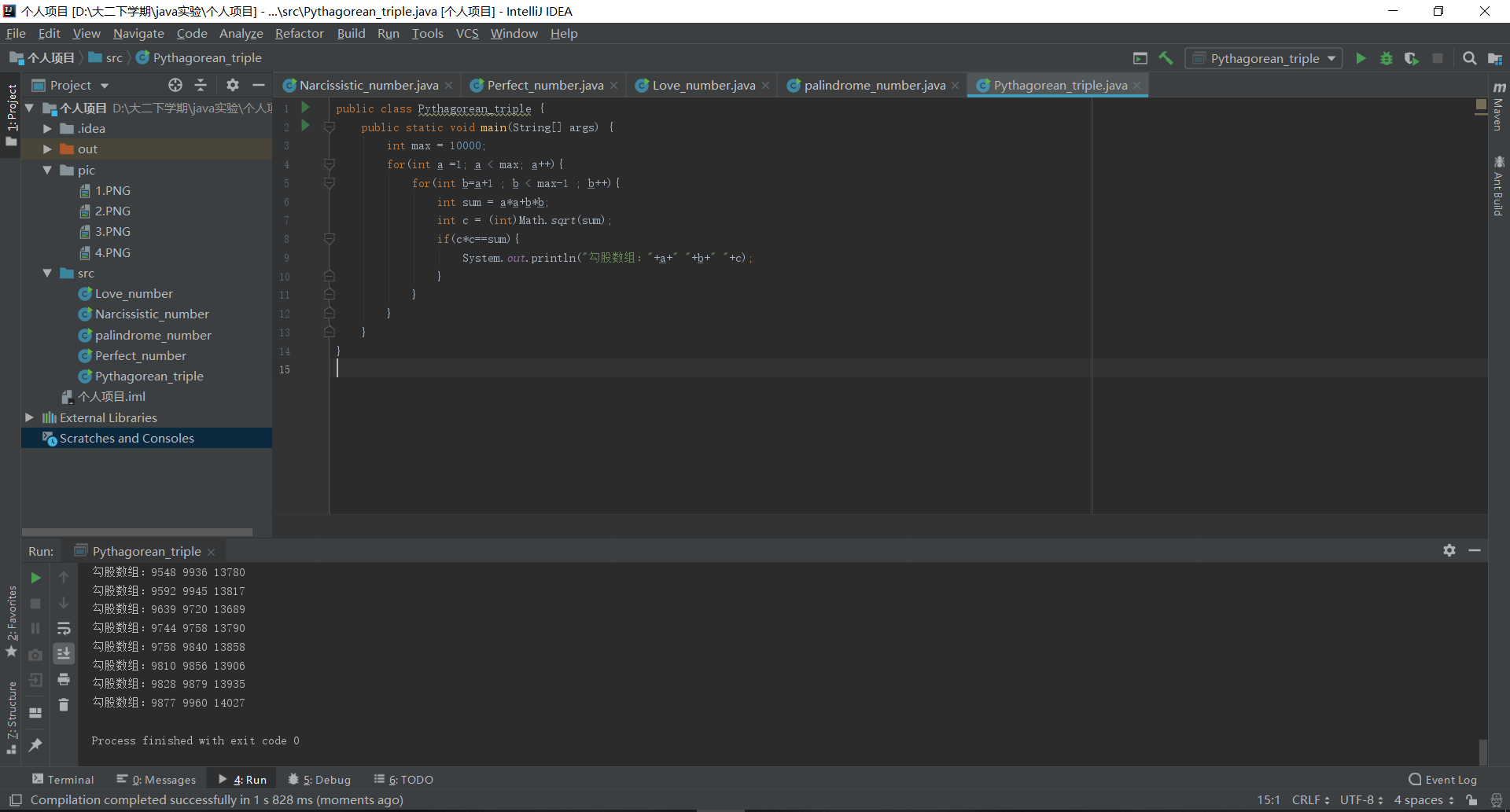
勾股数,又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。
public class Pythagorean_triple {
public static void main(String[] args) {
int max = 10000;
for(int a =1; a < max; a++){
for(int b=a+1 ; b < max-1 ; b++){
int sum = a*a+b*b;
int c = (int)Math.sqrt(sum);
if(c*c==sum){
System.out.println("勾股数组:"+a+" "+b+" "+c);
}
}
}
}
}
勾股数组的程序设计的思想是通过判断这个数是否是一个平方数的方法来确定勾股数组。
因为如果是一组勾股数组,那么a方和b方的加和的结果一定是一个平方数。
通过反证法,就可以判断了。
四方定理
“四方定理”是数论中著名的一个定理,指所有自然数至多只要用四个数的平方和就可以表示。
在手算的过程中,我发现一个数的四方定理并不是唯一解,所以我打算用穷举法来列举给定数的四方定理分解结果。
通过四次循环i,j,t,x来穷举i2+j2+t2+x2的方法来和键盘输入的num做比较,如果num==i2+j2+t2+x2,那么就输出这一组分解结果。
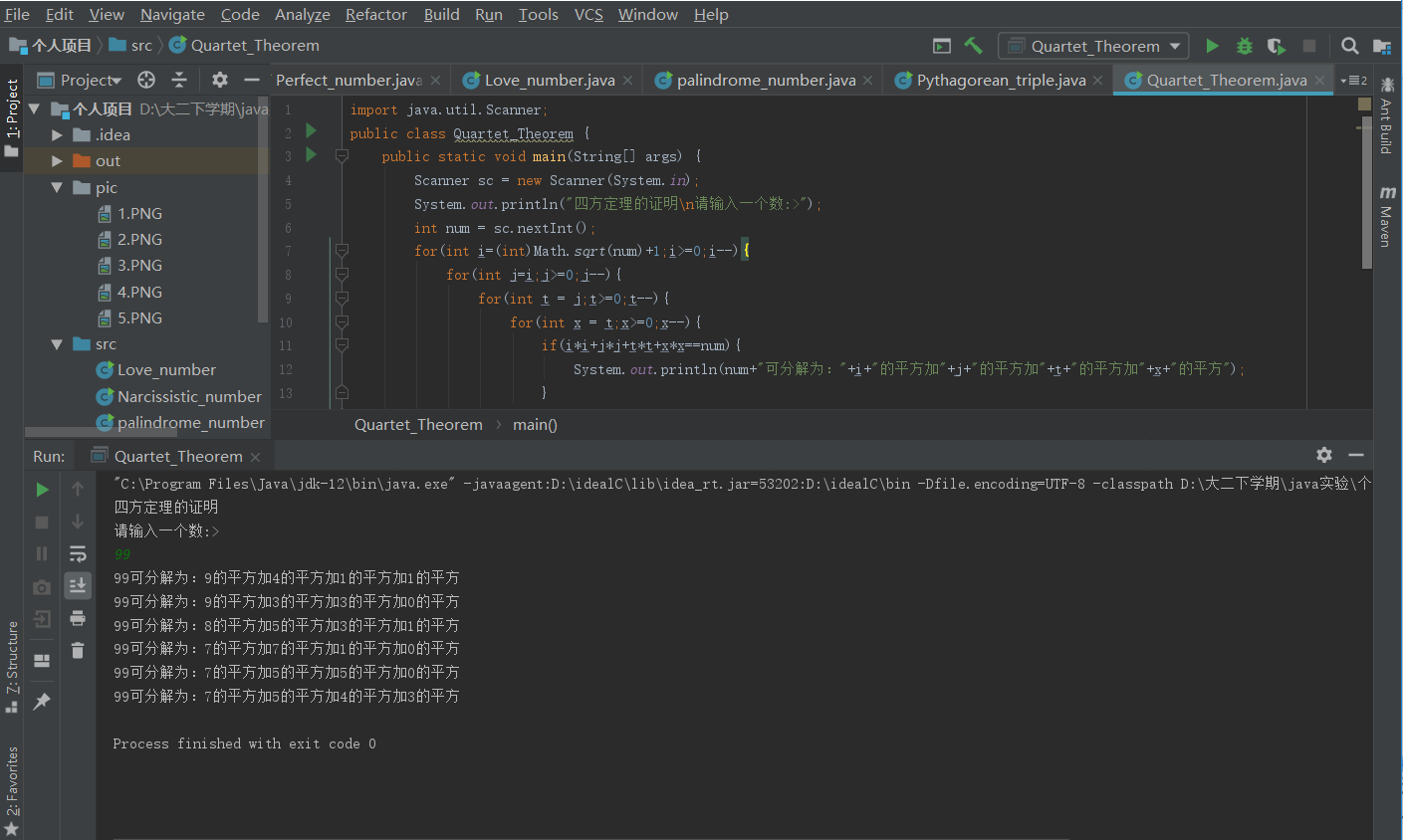
import java.util.Scanner;
public class Quartet_Theorem {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("四方定理的证明
请输入一个数:>");
int num = sc.nextInt();
for(int i=(int)Math.sqrt(num)+1;i>=0;i--){
for(int j=i;j>=0;j--){
for(int t = j;t>=0;t--){
for(int x = t;x>=0;x--){
if(i*i+j*j+t*t+x*x==num){
System.out.println(num+"可分解为:"+i+"的平方加"+j+"的平方加"+t+"的平方加"+x+"的平方");
}
}
}
}
}
}
}
尼科彻斯定理
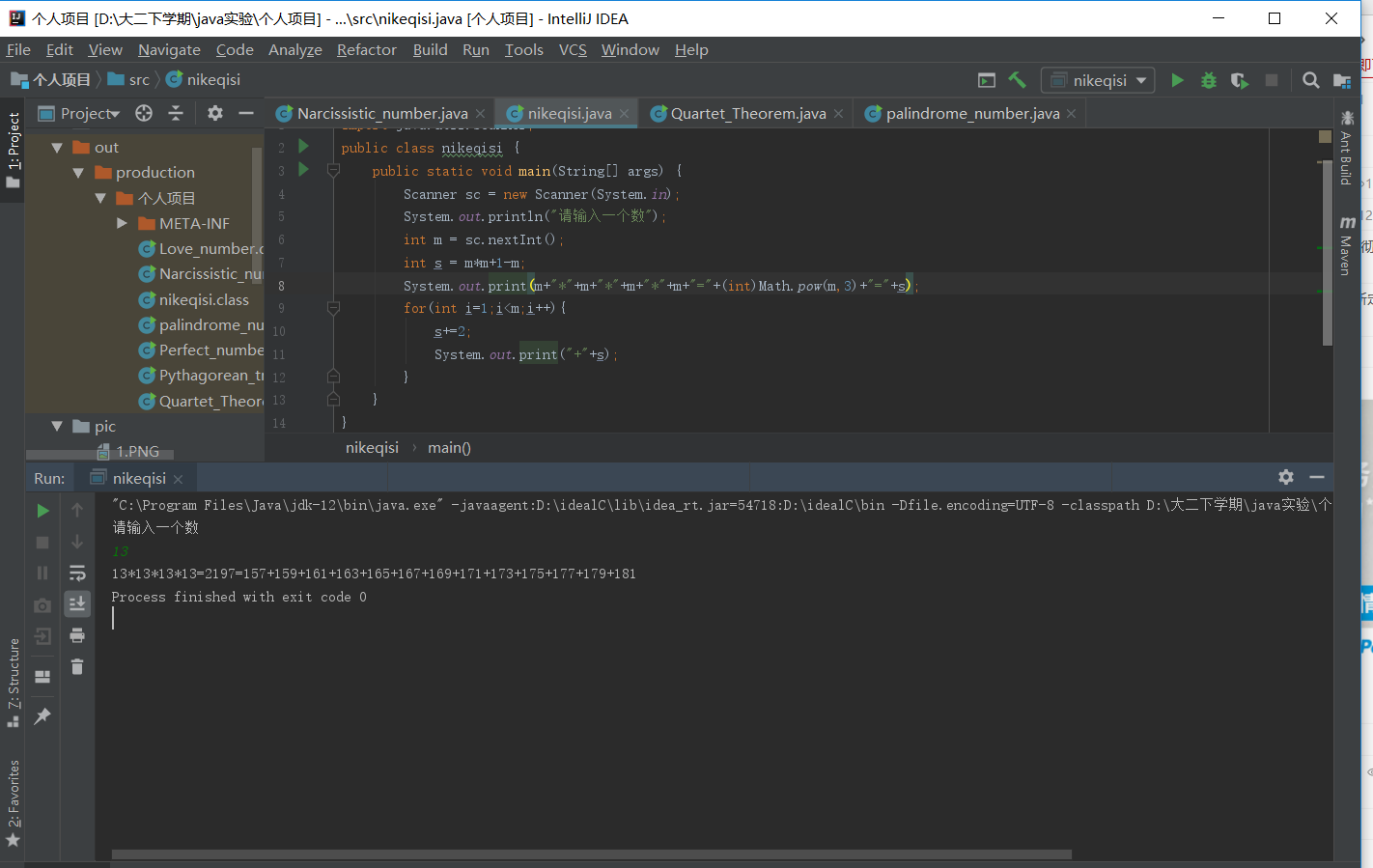
任何一个整数的立方都可以写成一串相邻奇数之和(因为如果不是一串相邻的奇数,这个奇数组合可能会有多个),这就是著名的尼科梅彻斯定理。
根据分析,一个数m的立方可以写成从mXm-m+1开始,m个奇数相加,根据这样的规律,先计算出s = mXm-m+1,再做一个循环输出就可以了。
import java.util.Scanner;
public class nikeqisi {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入一个数");
int m = sc.nextInt();
int s = m*m+1-m;
System.out.print(m+"*"+m+"*"+m+"*"+m+"="+(int)Math.pow(m,3)+"="+s);
for(int i=1;i<m;i++){
s+=2;
System.out.print("+"+s);
}
}
}