凸包

凸包的定义：

把平面内指定点全部包含的多边形（可以看成绳子围木桩）。

凸包的求法：

一. Graham扫描法

1.找到y坐标最小的点(如果有几个y坐标最小，就选其中x坐标最小的)，作为基点（H）。

2.把其他每个点到基点的线段与x轴的夹角，然后按这个夹角从小到大排序，然后逆时针扫一遍。

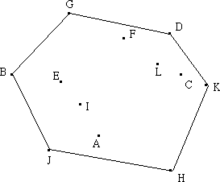
3.排序后依次是K,C,D,L,F,G,E,I,B,A,J。

4.首先是线段HK，假设他就在凸包上。然后我们扫到KC，因为HK到KC的旋转方向和我们开始扫过来的逆时针方向是相同的，所以我们假设KC也在凸包上。然后到了CD。现在问题来了，KC到CD的旋转方向不一致，所以我们确定C点不在凸包上。以此类推，等到点集中所有点遍历完成，我们就得到HKDGBJ几个凸包点。

5.总之确定某一个点是否在凸包上就依靠一个条件：上一个点连到该点的线段和该点连到下一个点的线段的旋转方向是否和开始扫描的方向相同（赤裸裸的凸包性质）。

 上代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
#define il inline
#define db double
using namespace std;
il int gi()
{
    int x=0,y=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
        y=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*y;
}
il ll gl()
{
    ll x=0,y=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
        y=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*y;
}
struct node
{
    db x,y;
};//点的结构体 
struct line
{
    node a,b;
};//两点的线段 
il db dis(node a,node b)
{
    db p1=(a.x-b.x)*(a.x-b.x);
    db p2=(a.y-b.y)*(a.y-b.y);
    return sqrt(p1+p2);
}//两点间的距离 
il db chaji(node a,node b,node c)
{
    db p1=(a.x-c.x)*(b.y-c.y);
    db p2=(b.x-c.x)*(a.y-c.y);
    return p1-p2;
}//三点叉积，如果大于零，则旋转方向为顺时针，小于零，则旋转方向为逆时针，等于零，共线。
il void Graham(node ps[],node ch[],int n,int &len)//ps是点集，ch是凸包栈，len记录凸包点数 
{
    int k=1,top=3;//top记录凸包的点有多少个 
    for(int i=1;i<=n;i++)//找出基点 
    if(ps[i].y==ps[k].y&&ps[i].x<ps[k].x)
    k=i;
    else
    if(ps[i].y<ps[k].y)
    k=i;
    swap(ps[1],ps[k]);//把基点放到ps[1] 
    for(int i=2;i<n;i++)//把所有点按极角排序，极角相同按到基点的距离排，冒泡排序 
    {
        k=i;
        for(int j=i+1;j<=n;j++)
        {
            if(chaji(ps[j],ps[k],ps[1])<0||(!chaji(ps[j],ps[k],ps[1])&&dis(ps[j],ps[1])<dis(ps[k],ps[1])))
            k=j;//
        }
        swap(ps[k],ps[i]);
    }
    ch[1]=ps[1];
    ch[2]=ps[2];
    ch[3]=ps[3];
    for(int i=4;i<=n;i++)
    {
        while(chaji(ps[i],ch[top],ch[top-1])<=0)
        top--;//递归处理来满足凸包的性质 
        ch[++top]=ps[i];//加入该点 
    }
    len=top;//记录凸包点数 
}
int main()
{
    return 0;
}