【问题描述】
山山在数学课上学到了平面上两点间直线距离公式:
山山对新的知识非常感兴趣,于是他上网查询了一下,发现他所学的叫做“欧几里得距
离(简称欧氏距离)
”

,还有一种距离叫“曼哈顿距离”,公式为:
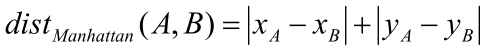
山山被这两个东西绕晕了。他开始尝试画一些点然后计算它们的这两种距离。发现有一
些点的欧氏距离和曼哈顿距离是相等的,他认为这个现象特别有趣。为了发现一些规律和性
质,他给出了 n 个点,想知道这些点中有多少对点的欧氏距离与曼哈顿距离相等。
由于山山还只是一名小学生,他的计算能力不是很强,于是他希望你能帮他算出这样的
点对数。 注意(A, B) 和(B, A) 被看作是相同的点对,只计算一次 。
【输入格式】
输入文件名为 geo.in。
第一行为一个正整数 n。
接下来 n 行每行两个整数 xi yi,表示每个点的坐标。
【输出格式】
输出文件名为 geo.out。
输出仅一行一个整数 ans 表示答案。 答案可能会很大,请使用 64 位整数。
【样例输入与输出】

【数据范围】
对于 20%的数据:0 < n <= 1000
对于 70%的数据:0 < n <= 100000,0 <= xi , yi <= 10 6 ,保证数据是随机生成的
对于 100%的数据:0 < n <= 100000,|xi |, |yi | <= 10 9
一开始我用的map做的这题,但是判重的时候用了离散化,结果细节没处理好,只拿了60分。
其实我们可以直接离散化,没必要用map。
代码:
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#define ll long long
#define il inline
#define db double
using namespace std;
il int gi()
{
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
y=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*y;
}
struct node
{
int x,y;
}c[200045];
bool cmp1(node a,node b)
{
return a.x<b.x;
}
bool cmp2(node a,node b)
{
if(a.y==b.y)
return a.x<b.x;
else
return a.y<b.y;
}
int main()
{
freopen("geo.in","r",stdin);
freopen("geo.out","w",stdout);
int n=gi();
for(int i=1;i<=n;i++)
c[i].x=gi(),c[i].y=gi();
sort(c+1,c+1+n,cmp1);
ll ans=0;
int now=c[1].x;
ll p=0;
for(int i=1;i<=n;i++)
{
if(c[i].x==now)
p++;
else
{
ans+=p*(p-1)/2;
now=c[i].x;
p=1;
}
}
if(p!=1)
ans+=p*(p-1)/2;
sort(c+1,c+1+n,cmp2);
now=c[1].y,p=0;
for(int i=1;i<=n;i++)
{
if(c[i].y==now)
p++;
else
{
ans+=p*(p-1)/2;
now=c[i].y;
p=1;
}
}
if(p!=1)
ans+=p*(p-1)/2;
int now1=c[1].x,now2=c[1].y;
p=0;
for(int i=1;i<=n;i++)
{
if(now1==c[i].x&&now2==c[i].y)
p++;
else
{
ans-=p*(p-1)/2;
now1=c[i].x,now2=c[i].y;
p=1;
}
}
if(p!=1)
ans-=p*(p-1)/2;
printf("%lld
",ans);
return 0;
}