三种直线段绘制方法：DDA算法、B算法和中点分割法

一、综述

三种直线段绘制方法：DDA算法、B算法和中点分割法。

在MFC环境中测试上述三种算法并对比分析三种算法的误差及效率。

二、程序框架

MFC程序：

cgDrawLineView.h为视图层的头文件，负责声明各种成员变量和成员函数；
cgDrawLineView.cpp为视图层的源文件，负责实现直线的三种绘制、误差分析及messageBox显示。
CSelectControl.h为窗口面板中的按键及文本定义成员变量及成员函数。
CSelectControl.cpp实现面板的功能，如点击按键绘制图像、分析误差等。

三、算法描述

1. DDA算法

原理：根据直线的微分方程计算dy=m*dx

（1）将给定端点作为输入参数；

（2）初始化，初值加上0.5确保精度；

（3）比较起止点水平和垂直的差值大数作为计算步数steps；

（4）每步计算dx，dy分别为差数除以steps；

（5）从起始点开始确定相邻两点间的增量并进行递推计算。

2. B算法

（1）设定interChange、Xsign、Ysign便于判断位置并计算误差初值e = 2 * min - max;（min和max分别为水平距离和垂直距离的最值）

（2）设置点(Xi, Yi) 的颜色值，并求下一误差ei+1；

​ 如果 ei >= 0 则ei+1 =ei+m-1；

​ 否则ei+1 = ei + m；

（3）根据不同象限，确定X和Y变化符号的正负，进行下一次（2）（3）循环直至结束；

3. 中点分割法

原理：递归二分法

结束条件：|P1-P2|<=1

（1）将直线段求中点坐标，若可以细分，则进行一次递归；

（2）如果中点坐标无法继续递归，则设置坐标的颜色值；

（3）执行至所有点都完成了颜色值的设置，程序结束。

四、处理流程

主要处理流程为：

1. 在DrawLineView.h中定义

   double ddaError, ddaSmooth, bError, bSmooth, mpError, mpSmooth;

   void MidPointline(CDC* pDC, float x1, float y1, float x2, float y2);

2. 在DrawLineView.cpp中完成初始赋值、函数具体实现以及误差、时间、平滑度计算和messageBox的弹出

3. 在IDD_SELECTCONTROL中新添加button（MidPoint Line）且添加类向导，完善void CCSelectControl::OnClickedMidpointline()函数

4. 在DrawLineView.cpp中完成pDoc->m_opMode ==2的调用程序基本完成

五、运行结果

当点击DDA Line时调用DDA直线生成函数

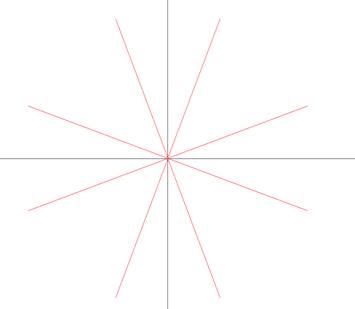
当点击B Line时调用B直线生成函数

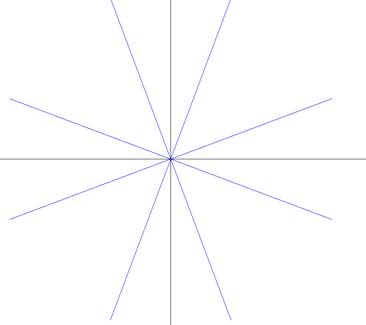
当点击MidPoint时调用中点分割直线生成函数

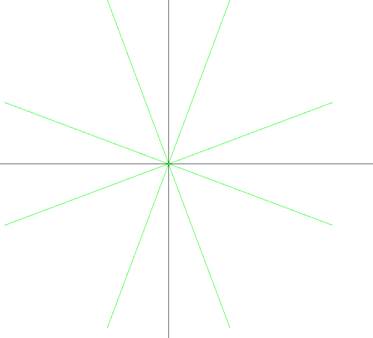
点击Comparision时先后调用三种直线生成函数，

并弹出调用时间（受限于电脑运行速度原因只运行单次，

计算次数for循环注释掉了，如有需要可取消注释，重新生成结果）、误差和光滑

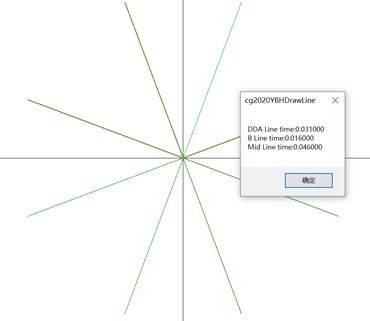
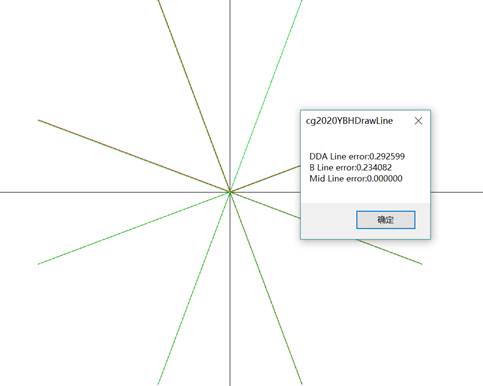
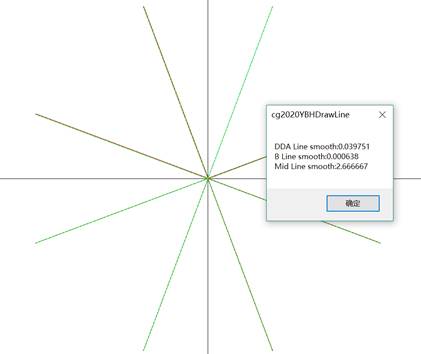
其中，RunTime值越低表示效率越高，Error越小表示误差越小，Smooth越小表示直线越光滑。

六、实验总结

1. 通过本次实验，首先我对VS的MFC有了一个初步了解与掌握

2. 对于三种常用的绘制直线算法: 数值微分(DDA)算法、中点算法、Bresenham算法有了更加深入的理解，特别是三种算法在绘制效率上的差别:

DDA算法: 复杂度：加法+取整

优点：避免了y=kx+b 方程中的浮点乘法。

缺点：需浮点数加法及取整运算，不利于硬件实现。

中点算法:

中点算法与DDA相比，主要是加法运算和浮点数运算，但是优化后，省去了浮点运算。

主要优点：算法简单，无乘除，只有移位操作，尤其适用硬件实现。

Bresenham算法：

相比之下，Bresenham算法是计算机图形学使用最广泛的直线光栅化算法。Bresenham算法是每个象素只需一个整数加法，其优点还有就是可以用于其他二次曲线。

3. 这次实验学生的主要困难在于如何实现信息的回显，起初因为对于这个名词的不太了解，上网查询时总是得不到想要的结果，因为主要搜索的内容是如何在新分割出来的窗口上显示文字内容，在上课询问过老师之后有了了解与理解，感觉问题不大，选择通过static Text来进行，静态的显示没有问题，但是运行后动态的回显总是完成失败，虽然失败但是多次尝试也让学生对于函数之间关系与彼此之间调用有了更好的理解，当时尝试更改的内容还有部分在源代码里注释掉了，可以查看痕迹，最后也没有实现static Text的回显，仿照老师给出资料完成messageBox信息弹出，之后实验课会认真了解static text回显信息的方法，而后进行改正，收获良多，谢谢。

核心代码：

DDA：

void Ccg2020YBHDrawLineView::DDAline(CDC* pDC, int x1, int y1, int x2, int y2)
{
  Ccg2020YBHDrawLineDoc* pDoc = GetDocument();
  int steps;
  float m, x, y, dx, dy;

  //误差分析
  double distance = 0.0;//生成点到理想直线的距离
  double kaverage = 0.0;//生成点和起点间斜率平均值

  x = x1 + 0.5f;
  y = y1 + 0.5f;
  steps = abs(x2 - x1) > abs(y2 - y1) ? abs(x2 - x1) : abs(y2 - y1);

  dx = (float)(x2 - x1) / steps;
  dy = (float)(y2 - y1) / steps;

  //计算直线斜率和截距
  m = (float)(y2 - y1) / (float)(x2 - x1);
  float b = y2 - m*x2;

  for (int i = 0; i < steps; i++) {
​    pDC->SetPixel((int)x + m_wndWidth / 2,
​       (int)(m_wndHeight / 2 - y), RGB(255, 0, 0));

​    //误差计算
​    distance += fabs(x*m + b - y) / sqrt(m*m + 1);
​    kaverage += fabs((y - y1) / (x - x1));

​    x += dx;
​    y += dy;

  }

  ddaError = distance / steps;
  ddaSmooth = fabs(kaverage / steps - m);

}

B:

void Ccg2020YBHDrawLineView::Bline(CDC* pDC, int x1, int y1, int x2, int y2)

{
  int x, y, dx, dy, e, xSign, ySign, interChange = 0;
  dx = abs(x2 - x1);
  dy = abs(y2 - y1);

  //误差分析
  double distance = 0.0f;//生成点到理想直线的距离
  double kaverage = 0.0f;//生成点和起点间斜率平均值

  //计算直线斜率和截距
  float m = (float)(y2 - y1) / (float)(x2 - x1);
  float b = y2 - m*x2;

  if (dx < dy) {
​    int temp;
​    interChange = 1;
​    temp = dx;
​    dx = dy;
​    dy = temp;
  }

  xSign = (x2 > x1) ? 1 : -1;
  ySign = (y2 > y1) ? 1 : -1;
  x = x1;
  y = y1;
  e = 2 * dy - dx;

    for (int i = 0; i <= dx; i++) {
​    pDC->SetPixel(x + m_wndWidth / 2,
​       m_wndHeight / 2 - y, RGB(0, 0, 255));

​    //误差计算
​    distance += fabs(x*m + b - y) / sqrt(m*m + 1);
​    if(x!=x1)
​    kaverage += fabs(y - y1) / fabs(x - x1);

​    if (e > 0) {
​       e = e - 2 * dx;
​       if (interChange)
​         x += xSign;
​       else
​         y += ySign;
​    }

​    if (interChange)
​       y += ySign;
​    else
​       x += xSign;
​    e = e + 2 * dy;

  }

  bError = distance / dx;
  bSmooth = fabs(kaverage / dx - m);

}

 

中点分割：

//利用递归原理，将（x1,y1）和（x2,y2）两点间的线段不断二分，
//直到分成的子线段的两个端点的距离小于一个像素，然后对子线段进行描绘。
void Ccg2020YBHDrawLineView::MidPointline(CDC* pDC, float x1, float y1, float x2, float y2)
{

  //误差分析
  double distance = 0.0f;//生成点到理想直线的距离
  double kaverage = 0.0f;//生成点和起点间斜率平均值
  float x = 0, y = 0;  
  int steps = fabs(x1 - x2) > fabs(y1 - y2) ? fabs(x1 - x2) : fabs(y1 - y2);

  //计算直线斜率和截距

  float m = (float)(y2 - y1) / (float)(x2 - x1);
  float b = y2 - m*x2;

  if (fabs(x1 - x2) <= 1 && fabs(y1 - y2) <= 1) {
​    pDC->SetPixel((int)((x1 + x2) / 2 )+ m_wndWidth / 2,
​       m_wndHeight / 2 - int((y1 + y2) / 2), RGB(0, 255, 0));
​    
​    //误差计算

​    x = (float)(x1 + x2) / 2;
​    y = (float)(y1 + y2) / 2;

​    distance += fabs(x*m + b - y) / sqrt(m*m + 1);
​    kaverage += fabs((y - y1) / (x - x1));
​    
  }

  else
  {
​    MidPointline(pDC, x1, y1, (x1 + x2) / 2, (y1 + y2) / 2);
​    MidPointline(pDC, (x1 + x2) / 2, (y1 + y2) / 2, x2, y2);
  }

  mpError = distance / steps;
  mpSmooth = fabs(kaverage / steps - m);

}