并查集

一、算法思想

　　并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。凡是涉及到元素的分组管理问题，都可以考虑使用并查集进行维护。

二、算法流程

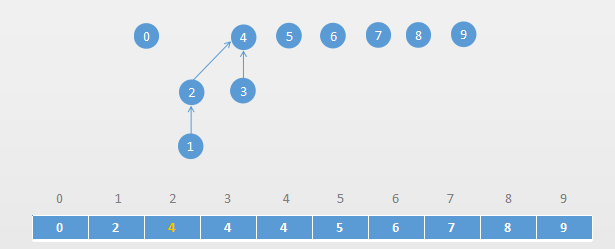
初始化

　　把每个点所在集合初始化为其自身。

　　通常来说，这个步骤在每次使用该数据结构时只需要执行一次，无论何种实现方式，时间复杂度均为O(N)。

查找

　　查找元素所在的集合，即根节点。

合并

　　将两个元素所在的集合合并为一个集合。

　　通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找”操作实现。

三、算法实现

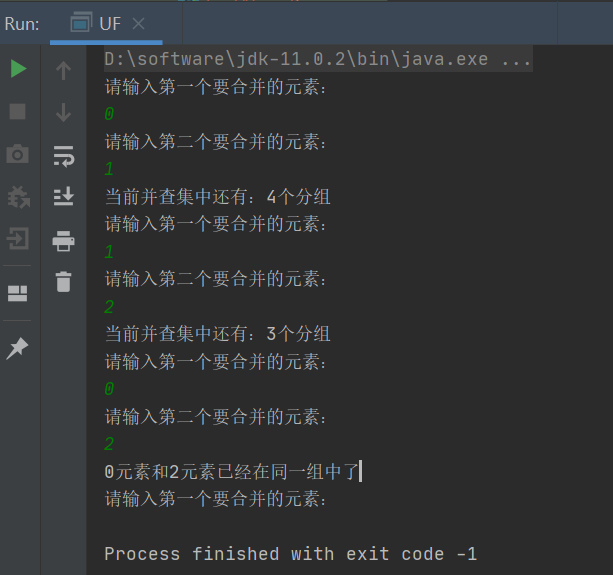
package io.guangsoft;

import java.util.Scanner;

public class UF {
    //记录节点元素和该元素所在分组的标志
    private int[] eleAndGroup;
    //记录并查集中数据的分组个数
    private int count;
    //用来存储每个根节点对应的树中保存的节点的个数
    private int[] sz;
    //初始化并查集，以整数标志(0，N-1)个节点
    public UF(int n) {
        //初始化分组数量，默认情况下，有n个分组
        this.count = n;
        //初始化eleAndGroup数组
        this.eleAndGroup = new int[n];
        //初始化eleAndGroup中元素及其所在组的标识符，让eleAndGroup数组中的索引作为并查集的每个节点的元素，并且让每个索引处的值（该元素所在组的标识符）就是该索引
        for(int i = 0; i < eleAndGroup.length; i++) {
            eleAndGroup[i] = i;
        }
        //默认情况下，sz中每个索引处的值都是1
        for(int i = 0; i < sz.length; i++) {
            sz[i] = 1;
        }
    }
    //获取当前并查集中有多少分组
    public int count() {
        return this.count;
    }
    //元素p所在分组的标识符
    public int find(int p) {
        while(true) {
            if(p == eleAndGroup[p]) {
                return p;
            }
            p = eleAndGroup[p];
        }
    }
    //判断并查集中元素p和元素q是否在同一分组
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    //把p元素所在分组和q元素所在分组合并
    public void union(int p, int q) {
        //找到p元素和q元素所在分组对应的树的根节点
        int pRoot = find(p);
        int qRoot = find(q);
        //如果p和q已经在同一分组，则不需要合并了
        if(pRoot == qRoot) return;
        //判断pRoot对应的树大还是qRoot对应的树大，最终需要把较小的树合并到较大的树中
        if(sz[pRoot] < sz[qRoot]) {
            eleAndGroup[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            eleAndGroup[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
        //组的数量-1
        this.count--;
    }
    //主类
    public static void main(String args[]) {
        //创建并查集对象
        UF uf = new UF(5);
        //从控制台录入两个要合并的元素，调用union方法合并，观察合并后并查集中分组是否减少
        Scanner sc = new Scanner(System.in);
        while(true) {
            System.out.println("请输入第一个要合并的元素：");
            int p = sc.nextInt();
            System.out.println("请输入第二个要合并的元素：");
            int q = sc.nextInt();
            //判断两个元素是否在同一组中了
            if(uf.connected(p, q)) {
                System.out.println(p + "元素和" + q + "元素已经在同一组中了");
                continue;
            }
            uf.union(p, q);
            System.out.println("当前并查集中还有：" + uf.count() + "个分组");
        }
    }
}

四、算法分析

在我们使用 Quick Union 版本的并查集使用树形结构来组织节点的关系。那么性能跟树的深度有关系，简称 O(h)，以前介绍二分搜索树的时候，时间复杂度也是为 O(h)。但是并查集并不是一个二叉树，而是一个多叉树，所以并查集的查询和合并时间复杂度并不是O(log n)，在加上rank和路径压缩优化后 ，并查集的时间复杂度为 O(log* n)