概念
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
哈夫曼编码,主要目的是根据使用频率来最大化节省字符(编码)的存储空间。霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。如果考虑到进一步节省存储空间,就应该将出现概率大(占比多)的字符用尽量少的0-1进行编码,也就是更靠近根(节点少),这也就是最优二叉树-哈夫曼树。
例题
有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,求这5个字符的哈夫曼编码,及压缩率。
解析
第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,3为生成的新节点,如图:
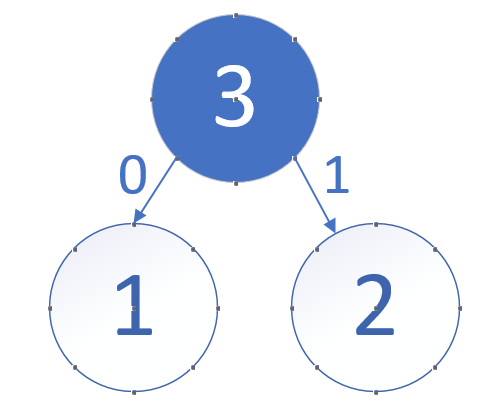
第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图:
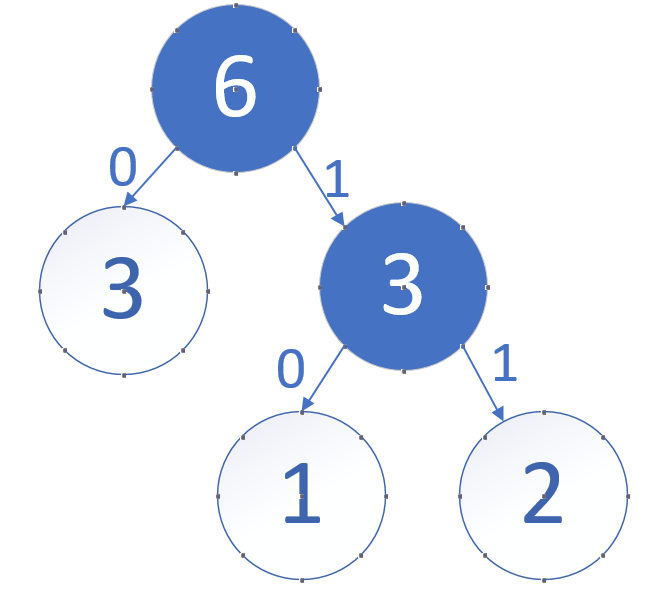
再依次建立哈夫曼树,得到最终哈夫曼树,如图:
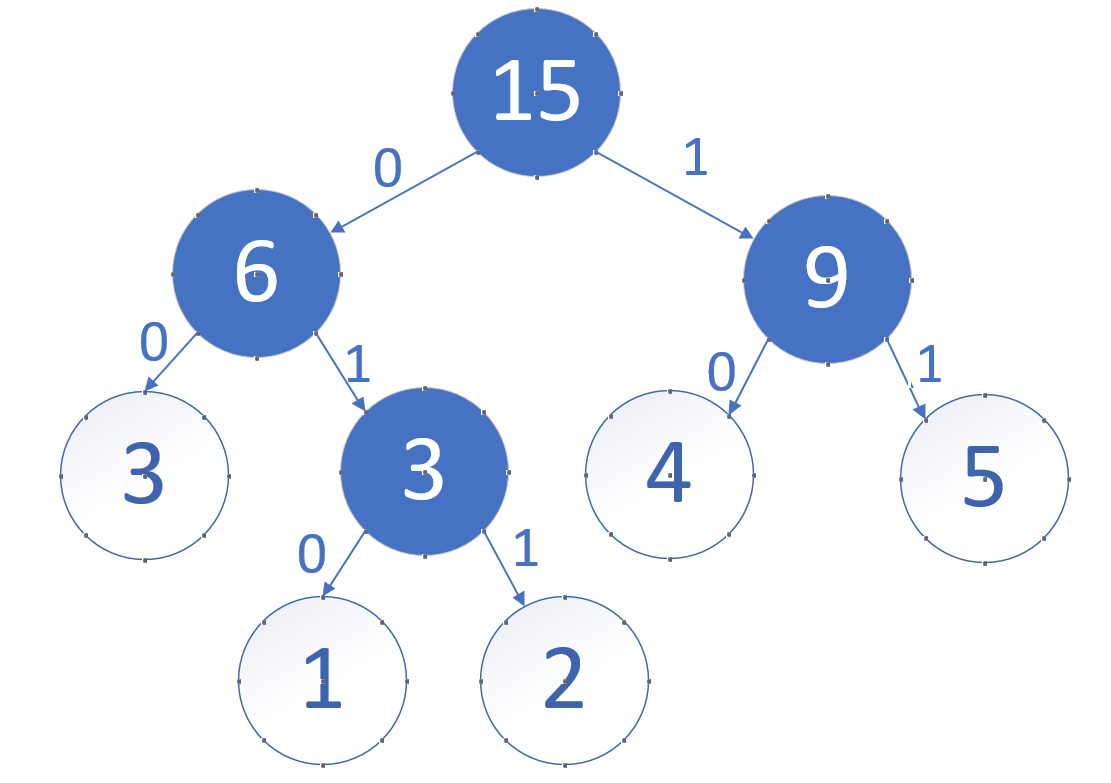
各个权值替换对应的字符,如下图:
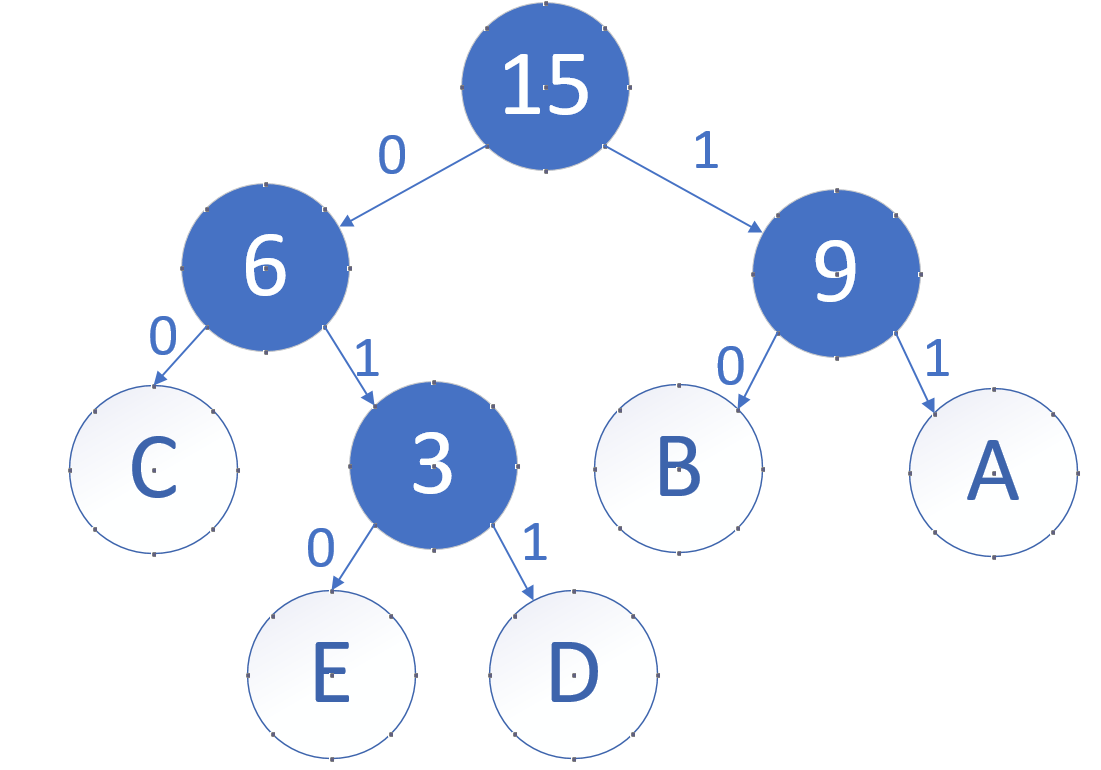
最终可以得出:
各字符对应的编码为:A->11,B->10,C->00,D->011,E->010
此文档(字符域)最终用三位二进行数进行的等长编码,平均长度为3
压缩率为(约等于):1 - (2 * 5 + 2 * 4 + 2 * 3 + 3 * 2 + 3 * 1 )/(3 * 15)= 25%