BP神经网络

摘要：神经网络就是在模拟人脑的结构组织，企图利用仿生学的知识解决问题。无可质疑人工智能和虚拟现实将成为最近几年的热点技术，虚拟现实的入门门槛较低，而人工智能的研究需要一定的知识水平，但无疑人工智能领域的每一个新的突破都将会深深的影响到未来的科技发展。
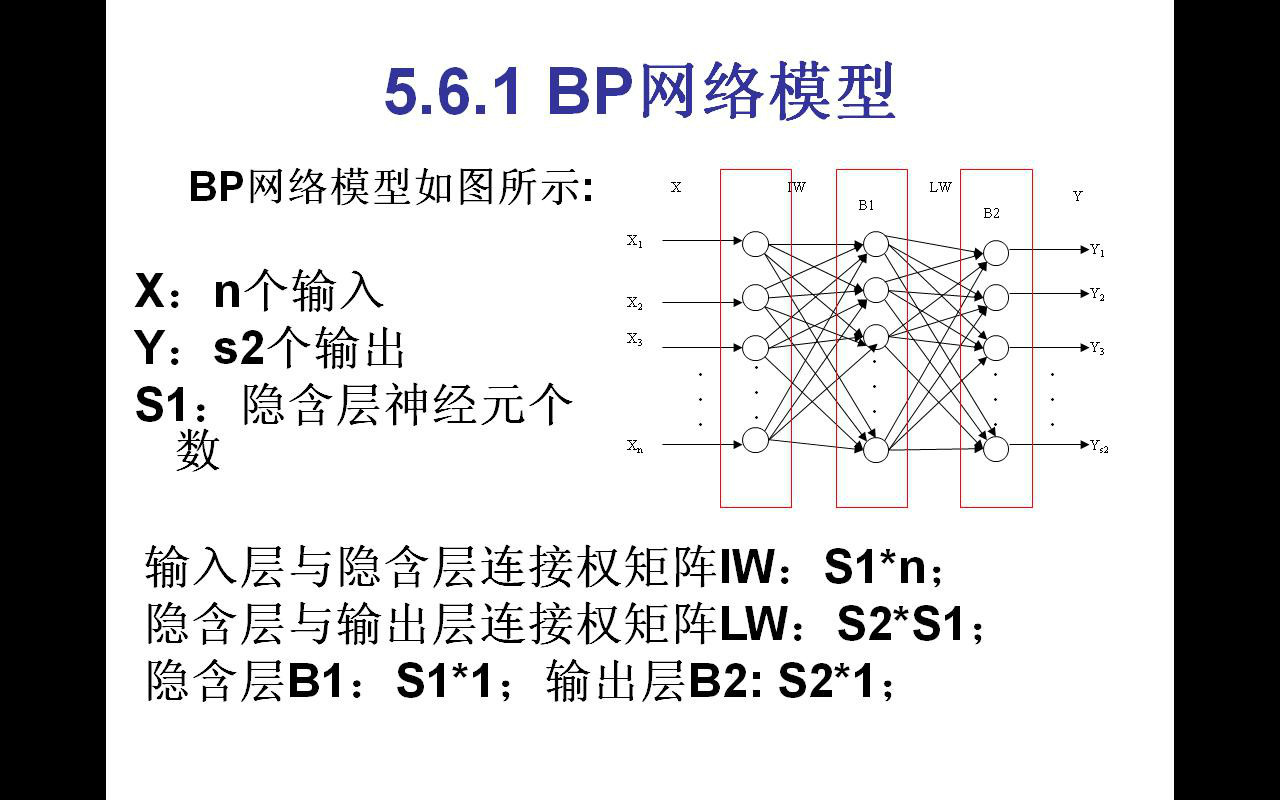
     BP（Back Propagation）神经网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用梯度下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层(hidden layer)和输出层(output layer)。

关键字：人工智能，神经网络，BP

The BP neural network

Abstract: the structure of the neural network is to simulate the human brain tissue, in an attempt to use the knowledge of bionics to solve problems. Undeniably artificial intelligence and virtual reality will become a hot technology in the recent years, virtual reality entry threshold is low, and artificial intelligence research needs certain levels of knowledge, but there is no doubt that every new breakthrough in the field of artificial intelligence will deeply affect the development of science and technology in the future.

BP (Back Propagation) neural network is a group of scientists headed by Rumelhart and McCelland 1986, is a kind of according to the error Back Propagation algorithm training of the multilayer feedforward network, is currently one of the most widely used neural network model. BP network can learn and store a lot of input - output model mapping, without prior reveal describe the mathematical equations of the mapping relationship. Its learning rule is to use gradient descent method, by back propagation to constantly adjust the network weights and threshold, minimize the error sum of squares of the network. BP neural network model of topological structures include input layer (input), the hidden layer, hidden layer) and output layer (output layer).

Keywords: artificial intelligence, neural network, BP

1，研究背景
  “人脑是如何工作的？”
     “人类能否制作模拟人脑的人工神经元？”

多少年以来，人们从医学、生物学、生理学、哲学、信息学、计算机科学、认知学、组织协同学等各个角度企图认识并解答上述问题。在寻找上述问题答案的研究过程中，逐渐形成了一个新兴的多学科交叉技术领域，称之为“神经网络”。神经网络的研究涉及众多学科领域，这些领域互相结合、相互渗透并相互推动。不同领域的科学家又从各自学科的兴趣与特色出发，提出不同的问题，从不同的角度进行研究。

心理学家和认知科学家研究神经网络的目的在于探索人脑加工、储存和搜索信息的机制，弄清人脑功能的机理，建立人类认知过程的微结构理论。

生物学、医学、脑科学专家试图通过神经网络的研究推动脑科学向定量、精确和理论化体系发展，同时也寄希望于临床医学的新突破；信息处理和计算机科学家研究这一问题的目的在于寻求新的途径以解决不能解决或解决起来有极大困难的大量问题，构造更加逼近人脑功能的新一代计算机。

2，研究方向
   

•I->H （输入层à隐含层）

  a 1 = tansig (IW 1,1 p 1 +b 1 )

  tansig(x)=tanh(x)=(ex-e-x)/(ex+e-x)

•H->O （隐含层à输出层）

  a 2 = purelin (LW 2,1 a 1 +b 2 )

•输入层神经元个数  n

•隐含层神经元个数  s1

•输出层神经元个数  s2

•输入q组样本  p1,p2,...,pq    pi∈Rn

•期望输出 T1,T2,...,Tq,     T ∈Rs1

•网络输出  a21,a22,...,a2q  a2∈Rs2

•解决方法  误差最小

•实质为一个优化问题

•思路1: 梯度法(gradient)

•找出误差与加权系数的关系

•得到加权系数改变的规律

•输出层误差 ej(j=1，2，…，s2)

•隐含层误差 ei(i=1，2，…，n1)

•ei与ej的关系？

•ei可以认为是由ej加权组合形成的。由于作用函数的存在，ej的等效作用为δj =ejf '()

 

3，程序设计

   

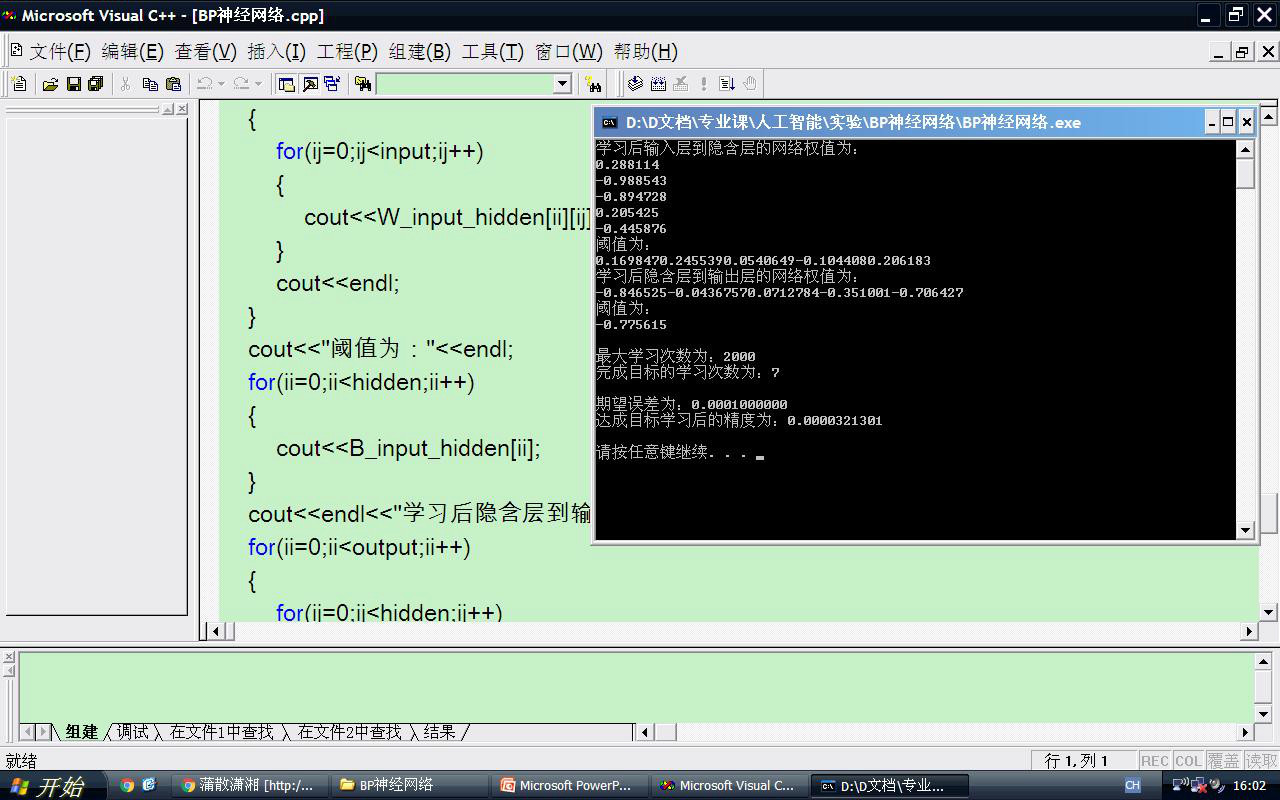
#include<iostream>
#include<cstdlib>
#include<fstream>
#include<ctime>
#include<cmath>
#include<iomanip>
using namespace std;

const int max_learn_length = 2000;      //最大学习次数
const double study_rate = 0.01;          //学习率(数据调整步长值)
const double anticipation_error = 0.0001;  //期望误差
const int input = 1;                    //每组样本输入层数据量
const int hidden = 5;                   //每组样本隐含层数据量
const int output = 1;                   //每组样本输出层数据量

int sample;                      //样本数量
double *P;                //输入矢量
double *T;                //输出矢量

void readfile()
{
    fstream p,t;
    p.open("p.txt",ios::in);
    t.open("t.txt",ios::in);
    if(!p||!t)
    {
        cout<<"file load failed!"<<endl;
        exit(0);
    }
    p>>sample;
    t>>sample;
    P=new double[sample];
    T=new double[sample];
    for(int ii=0;!p.eof()&&!t.eof();ii++)
    {
        p>>P[ii];
        t>>T[ii];
    }
    p.close();
    t.close();
}

void displaydata()
{
    cout<<"sample="<<sample<<endl;
    cout<<setiosflags(ios::fixed)<<setprecision(6);
    for(int ii=0;ii<sample;ii++)
    {
        cout<<"P["<<ii<<"]="<<P[ii]<<" T["<<ii<<"]="<<T[ii]<<endl;
    }
}

int main(int argc, char **argv)
{
    double precision;                           //误差精度变量
    double W_input_hidden[hidden][input];       //输入层到隐含层的网络权值变量
    double W_hidden_output[output][hidden];     //隐含层到输出层的网络权值变量
    double B_input_hidden[hidden];              //输入层到隐含层阈值变量
    double B_hidden_output[output];             //隐含层到输出层阈值变量
    double E_input_hidden[hidden];              //输入层到隐含层误差
    double E_hidden_output[output];             //隐含层到输出层误差
    double A_input_hidden[hidden];                    //隐含层实际输出值
    double A_hidden_output[output];                    //输出层实际输出值
    int ii, ij, ik, ic;

    readfile();
    displaydata();

    srand(time(0));                            //初始化随机函数

    for (ii = 0; ii<hidden; ii++)
    {
        B_input_hidden[ii] = 2 * (double)rand() / RAND_MAX - 1;  //阈值变量赋随机值(-1,1)
        for (ij = 0; ij<input; ij++)                             //网络权值变量赋随机值 
        {
            W_input_hidden[ii][ij] = 2 * (double)rand() / RAND_MAX - 1;
        }
    }
    for (ii = 0; ii<output; ii++)
    {
        B_hidden_output[ii] = 2 * (double)rand() / RAND_MAX - 1;  //阈值变量赋随机值(-1,1)
        for (ij = 0; ij<hidden; ij++)                             //网络权值变量赋随机值 
        {
            W_hidden_output[ii][ij] = 2 * (double)rand() / RAND_MAX - 1;
        }
    }

    precision = INT_MAX ;                      //初始化精度值
    for (ic = 0; ic < max_learn_length; ic++)  //最大学习次数内循环
    {
        if (precision<anticipation_error)      //循环剪枝函数
        {
            break;
        }
        precision = 0;
        for (ii = 0; ii<sample; ii++)          //21组样本循环叠加误差精度
        {
            for (ij = 0; ij<hidden; ij++)      //输入层到隐含层的输出计算
            {
                A_input_hidden[ij] = 0.0;
                for (ik = 0; ik<input; ik++)  
                {
                    A_input_hidden[ij] += P[ik] * W_input_hidden[ij][ik];
                }
                A_input_hidden[ij] += B_input_hidden[ij];
                A_input_hidden[ij]=(double)2/(1+exp(-2*A_input_hidden[ij]))-1;
            }
            for (ij = 0; ij<output; ij++)      //中间层到输出层的输出计算
            {
                A_hidden_output[ij] = 0.0;
                for (ik = 0; ik<hidden; ik++)  
                {
                    A_hidden_output[ij] += A_input_hidden[ik] * W_hidden_output[ij][ik];
                }
                A_hidden_output[ij] += B_hidden_output[ij];
            }

            for(ij=0;ij<output;ij++)           //隐含层到输出层的误差效能计算
            {
                E_hidden_output[ij]=T[ij]-A_hidden_output[ij];
            }
            for(ij=0;ij<hidden;ij++)           //输入层到隐含层的误差效能计算
            {
                E_input_hidden[ij]=0.0;
                for(ik=0;ik<output;ik++)
                {
                    E_input_hidden[ij]+=E_hidden_output[ik]*W_hidden_output[ik][ij];
                }
                E_input_hidden[ij]=E_input_hidden[ij]*(1-A_input_hidden[ij]);
            }

            for (ij = 0; ij<output; ij++)      //通过学习率调整隐含层到输出层的网络权值和阈值
            {
                for (ik = 0; ik<hidden; ik++)
                {
                    W_hidden_output[ij][ik] += study_rate*E_hidden_output[ij]*A_input_hidden[ik];
                }
                B_hidden_output[ij] += study_rate*E_hidden_output[ij];
            }
            for (ij = 0; ij<hidden; ij++)      //通过学习率调整输入层到隐含层的网络权值和阈值
            {
                for (ik = 0; ik<input; ik++)
                {
                    W_input_hidden[ij][ik] += study_rate*E_input_hidden[ij]*P[ik];
                }
                B_input_hidden[ij] += study_rate*E_input_hidden[ij];
            }

            for (ij = 0; ij<output; ij++)   //计算误差精度
            {
                precision += pow((T[ij] - A_hidden_output[ij]),2);
            }
        }
    }
    cout<<"学习后输入层到隐含层的网络权值为："<<endl;
    for(ii=0;ii<hidden;ii++)
    {
        for(ij=0;ij<input;ij++)
        {
            cout<<W_input_hidden[ii][ij];
        }
        cout<<endl;
    }
    cout<<"阈值为："<<endl;
    for(ii=0;ii<hidden;ii++)
    {
        cout<<B_input_hidden[ii];
    }
    cout<<endl<<"学习后隐含层到输出层的网络权值为："<<endl;
    for(ii=0;ii<output;ii++)
    {
        for(ij=0;ij<hidden;ij++)
        {
            cout<<W_hidden_output[ii][ij];
        }
        cout<<endl;
    }
    cout<<"阈值为："<<endl;
    for(ii=0;ii<output;ii++)
    {
        cout<<B_hidden_output[ii];
    }
    cout<<endl<<endl;
    cout <<"最大学习次数为：" << max_learn_length << endl;
    cout << "完成目标的学习次数为：" << ic << endl;
    cout << endl << "期望误差为：" <<setiosflags(ios::fixed)
        <<setprecision(10)<< anticipation_error << endl;
    cout << "达成目标学习后的精度为：" << precision <<endl<< endl;
    system("pause");
    return 0;
}

p.txt

21
-1
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1

t.txt

21
-0.9602
-0.5770
-0.0729
0.3771
0.6405
0.6600
0.4609
0.1336
-0.2013
-0.4344
-0.5000
-0.3930
-0.1647
0.0988
0.3072
0.3960
0.3449
0.1816
-0.0312
-0.2189
-0.3201