转载地址:http://www.gcssloop.com/customview/Path_Basic/
安卓自定义View进阶-Path之基本操作
在上一篇Canvas之图片文字中我们了解了如何使用Canvas中绘制图片文字,结合前几篇文章,Canvas的基本操作已经差不多完结了,然而Canvas不仅仅具有这些基本的操作,还可以更加炫酷,本次会了解到path(路径)这个Canvas中的神器,有了这个神器,就能创造出更多炫(zhuang)酷(B)的东东了。
一.Path常用方法表
为了兼容性(偷懒) 本表格中去除了部分API21(即安卓版本5.0)以上才添加的方法。
| 作用 | 相关方法 | 备注 |
|---|---|---|
| 移动起点 | moveTo | 移动下一次操作的起点位置 |
| 设置终点 | setLastPoint | 重置当前path中最后一个点位置,如果在绘制之前调用,效果和moveTo相同 |
| 连接直线 | lineTo | 添加上一个点到当前点之间的直线到Path |
| 闭合路径 | close | 连接第一个点连接到最后一个点,形成一个闭合区域 |
| 添加内容 | addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo | 添加(矩形, 圆角矩形, 椭圆, 圆, 路径, 圆弧) 到当前Path,addPath添加一个path (注意addArc和arcTo的区别) |
| 是否为空 | isEmpty | 判断Path是否为空 |
| 是否为矩形 | isRect | 判断path是否是一个矩形 |
| 替换路径 | set | 用新的路径替换到当前路径所有内容 |
| 偏移路径 | offset | 对当前路径之前的操作进行偏移(不会影响之后的操作) |
| 贝塞尔曲线 | quadTo, cubicTo | 分别为二次和三次贝塞尔曲线的方法 |
| rXxx方法 | rMoveTo, rLineTo, rQuadTo, rCubicTo | 不带r的方法是基于原点的坐标系(偏移量), rXxx方法是基于当前点坐标系(偏移量) |
| 填充模式 | setFillType, getFillType, isInverseFillType, toggleInverseFillType | 设置,获取,判断和切换填充模式 |
| 提示方法 | incReserve | 提示Path还有多少个点等待加入(这个方法貌似会让Path优化存储结构) |
| 布尔操作(API19) | op | 对两个Path进行布尔运算(即取交集、并集等操作) |
| 计算边界 | computeBounds | 计算Path的边界 |
| 重置路径 | reset, rewind | 清除Path中的内容 reset不保留内部数据结构,但会保留FillType. rewind会保留内部的数据结构,但不保留FillType |
| 矩阵操作 | transform | 矩阵变换 |
二.Path详解
请关闭硬件加速,以免引起不必要的问题!
请关闭硬件加速,以免引起不必要的问题!
请关闭硬件加速,以免引起不必要的问题!
在AndroidMenifest文件中application节点下添上 android:hardwareAccelerated=”false”以关闭整个应用的硬件加速。
更多请参考这里:Android的硬件加速及可能导致的问题
Path作用
本次特地开了一篇详细讲解Path,为什么要单独摘出来呢,这是因为Path在2D绘图中是一个很重要的东西。
在前面我们讲解的所有绘制都是简单图形(如 矩形 圆 圆弧等),而对于那些复杂一点的图形则没法去绘制(如绘制一个心形 正多边形 五角星等),而使用Path不仅能够绘制简单图形,也可以绘制这些比较复杂的图形。另外,根据路径绘制文本和剪裁画布都会用到Path。
关于Path的作用先简单地说这么多,具体的我们接下来慢慢研究。
Path含义
官方介绍:
The Path class encapsulates compound (multiple contour) geometric paths consisting of straight line segments, quadratic curves, and cubic curves. It can be drawn with canvas.drawPath(path, paint), either filled or stroked (based on the paint’s Style), or it can be used for clipping or to draw text on a path.
嗯,没错依旧是拿来装逼的,如果你看不懂的话,不用担心,其实并没有什么卵用。
通俗解释(sloop个人版):
Path封装了由直线和曲线(二次,三次贝塞尔曲线)构成的几何路径。你能用Canvas中的drawPath来把这条路径画出来(同样支持Paint的不同绘制模式),也可以用于剪裁画布和根据路径绘制文字。我们有时会用Path来描述一个图像的轮廓,所以也会称为轮廓线(轮廓线仅是Path的一种使用方法,两者并不等价)
另外路径有开放和封闭的区别。
| 图像 | 名称 | 备注 |
|---|---|---|
 |
封闭路径 | 首尾相接形成了一个封闭区域 |
 |
开放路径 | 没有首位相接形成封闭区域 |
这个是我随便画的,仅为展示一下区别,请无视我灵魂画师一般的绘图水准。
与Path相关的还有一些比较神奇的概念,不过暂且不说,等接下来需要用到的时候再详细说明。
Path使用方法详解
前面扯了一大堆概念性的东西。接下来就开始实战了,请诸位看官准备好瓜子、花生、爆米花,坐下来慢慢观看。
第1组: moveTo、 setLastPoint、 lineTo 和 close
由于Path的有些知识点无法单独来讲,所以本次采取了一次讲一组方法。
按照惯例,先创建画笔:
Paint mPaint = new Paint(); // 创建画笔 mPaint.setColor(Color.BLACK); // 画笔颜色 - 黑色 mPaint.setStyle(Paint.Style.STROKE); // 填充模式 - 描边 mPaint.setStrokeWidth(10); // 边框宽度 - 10
lineTo:
方法预览:
publicvoidlineTo(floatx,floaty)
首先讲解的的LineTo,为啥先讲解这个呢?
是因为moveTo、 setLastPoint、 close都无法直接看到效果,借助有具现化效果的lineTo才能让这些方法现出原形。
lineTo很简单,只有一个方法,作用也很容易理解,line嘛,顾名思义就是一条线。
俗话(数学书上)说,两点确定一条直线,但是看参数明显只给了一个点的坐标吧(这不按常理出牌啊)。
再仔细一看,这个lineTo除了line外还有一个to呢,to翻译过来就是“至”,到某个地方的意思,lineTo难道是指从某个点到参数坐标点之间连一条线?
没错,你猜对了,但是这某个点又是哪里呢?
前面我们提到过Path可以用来描述一个图像的轮廓,图像的轮廓通常都是用一条线构成的,所以这里的某个点就是上次操作结束的点,如果没有进行过操作则默认点为坐标原点。
那么我们就来试一下:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心(宽高数据在onSizeChanged中获取) Path path = new Path(); // 创建Path path.lineTo(200, 200); // lineTo path.lineTo(200,0); canvas.drawPath(path, mPaint); // 绘制Path
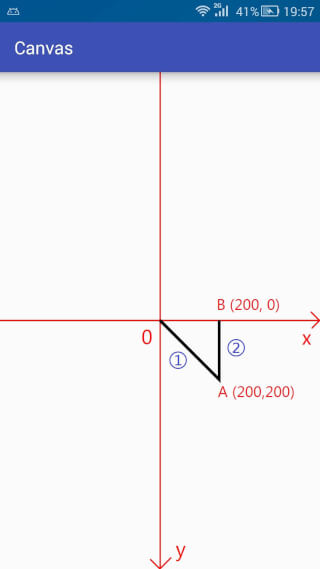
在示例中我们调用了两次lineTo,第一次由于之前没有过操作,所以默认点就是坐标原点O,结果就是坐标原点O到A(200,200)之间连直线(用蓝色圈1标注)。
第二次lineTo的时候,由于上次的结束位置是A(200,200),所以就是A(200,200)到B(200,0)之间的连线(用蓝色圈2标注)。
moveTo 和 setLastPoint:
方法预览:
// moveTo publicvoidmoveTo(floatx,floaty)// setLastPointpublicvoidsetLastPoint(floatdx,floatdy)
这两个方法虽然在作用上有相似之处,但实际上却是完全不同的两个东东,具体参照下表:
| 方法名 | 简介 | 是否影响之前的操作 | 是否影响之后操作 |
|---|---|---|---|
| moveTo | 移动下一次操作的起点位置 | 否 | 是 |
| setLastPoint | 设置之前操作的最后一个点位置 | 是 | 是 |
废话不多说,直接上代码:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 Path path = new Path(); // 创建Path path.lineTo(200, 200); // lineTo path.moveTo(200,100); // moveTo path.lineTo(200,0); // lineTo canvas.drawPath(path, mPaint); // 绘制Path

这个和上面演示lineTo的方法类似,只不过在两个lineTo之间添加了一个moveTo。
moveTo只改变下次操作的起点,在执行完第一次LineTo的时候,本来的默认点位置是A(200,200),但是moveTo将其改变成为了C(200,100),所以在第二次调用lineTo的时候就是连接C(200,100) 到 B(200,0) 之间的直线(用蓝色圈2标注)。
下面是setLastPoint的示例:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 Path path = new Path(); // 创建Path path.lineTo(200, 200); // lineTo path.setLastPoint(200,100); // setLastPoint path.lineTo(200,0); // lineTo canvas.drawPath(path, mPaint); // 绘制Path
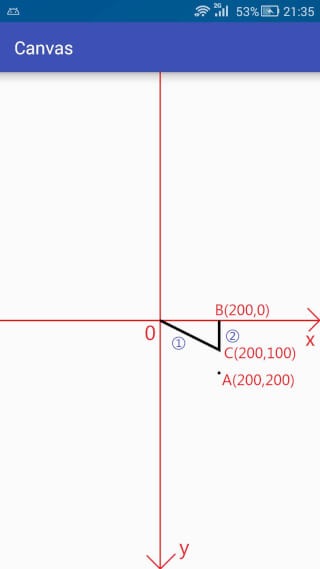
setLastPoint是重置上一次操作的最后一个点,在执行完第一次的lineTo的时候,最后一个点是A(200,200),而setLastPoint更改最后一个点为C(200,100),所以在实际执行的时候,第一次的lineTo就不是从原点O到A(200,200)的连线了,而变成了从原点O到C(200,100)之间的连线了。
在执行完第一次lineTo和setLastPoint后,最后一个点的位置是C(200,100),所以在第二次调用lineTo的时候就是C(200,100) 到 B(200,0) 之间的连线(用蓝色圈2标注)。
close
方法预览:
publicvoidclose()close方法用于连接当前最后一个点和最初的一个点(如果两个点不重合的话),最终形成一个封闭的图形。
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 Path path = new Path(); // 创建Path path.lineTo(200, 200); // lineTo path.lineTo(200,0); // lineTo path.close(); // close canvas.drawPath(path, mPaint); // 绘制Path

很明显,两个lineTo分别代表第1和第2条线,而close在此处的作用就算连接了B(200,0)点和原点O之间的第3条线,使之形成一个封闭的图形。
注意:close的作用是封闭路径,与连接当前最后一个点和第一个点并不等价。如果连接了最后一个点和第一个点仍然无法形成封闭图形,则close什么 也不做。
第2组: addXxx与arcTo
这次内容主要是在Path中添加基本图形,重点区分addArc与arcTo。
第一类(基本形状)
方法预览:
// 第一类(基本形状) // 圆形 public void addCircle(floatx,floaty,floatradius,Path.Directiondir)// 椭圆 public void addOval(RectFoval,Path.Directiondir)// 矩形 public void addRect(floatleft,floattop,floatright,floatbottom,Path.Directiondir) public void addRect(RectFrect,Path.Directiondir)// 圆角矩形 public void addRoundRect(RectFrect,float[]radii,Path.Directiondir)publicvoidaddRoundRect(RectFrect,floatrx,floatry,Path.Directiondir)
这一类就是在path中添加一个基本形状,基本形状部分和前面所讲的绘制基本形状并无太大差别,详情参考Canvas之绘制图形, 本次只将其中不同的部分摘出来详细讲解一下。
仔细观察一下第一类是方法,无一例外,在最后都有一个 Path.Direction,这是一个什么神奇的东东?
Direction的意思是 方向,趋势。 点进去看一下会发现Direction是一个枚举(Enum)类型,里面只有两个枚举常量,如下:
| 类型 | 解释 | 翻译 |
|---|---|---|
| CW | clockwise | 顺时针 |
| CCW | counter-clockwise | 逆时针 |
瞬间懵逼,我只是想添加一个基本的形状啊,搞什么顺时针和逆时针, (╯‵□′)╯︵┻━┻
稍安勿躁,┬─┬ ノ( ‘ - ‘ノ) {摆好摆好) 既然存在肯定是有用的,先偷偷剧透一下这个顺时针和逆时针的作用。
| 序号 | 作用 |
|---|---|
| 1 | 在添加图形时确定闭合顺序(各个点的记录顺序) |
| 2 | 对图形的渲染结果有影响(是判断图形渲染的重要条件) |
这个先剧透这么多,至于对闭合顺序有啥影响,图形的渲染等问题等请慢慢看下去
咱们先研究确定闭合顺序的问题,添加一个矩形试试看:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 Path path = new Path(); path.addRect(-200,-200,200,200, Path.Direction.CW); canvas.drawPath(path,mPaint);

将上面代码的CW改为CCW再运行一次。接下来就是见证奇迹的时刻,两次运行结果一模一样,有木有很神奇!
(╯°Д°)╯︵ ┻━┻(再TM掀一次) 坑人也不带这样的啊,一毛一样要它干嘛。
其实啊,这个东东是自带隐身技能的,想要让它现出原形,就要用到咱们刚刚学到的setLastPoint(重置当前最后一个点的位置)。
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 Path path = new Path(); path.addRect(-200,-200,200,200, Path.Direction.CW); path.setLastPoint(-300,300); // <-- 重置最后一个点的位置 canvas.drawPath(path,mPaint);

可以明显看到,图形发生了奇怪的变化。为何会如此呢?
我们先分析一下,绘制一个矩形(仅绘制边线),实际上只需要进行四次lineTo操作就行了,也就是说,只需要知道4个点的坐标,然后使用moveTo到第一个点,之后依次lineTo就行了(从上面的测试可以看出,在实际绘制中也确实是这么干的)。
可是为什么要这么做呢?确定一个矩形最少需要两个点(对角线的两个点),根据这两个点的坐标直接算出四条边然后画出来不就行了,干嘛还要先计算出四个点坐标,之后再连直线呢?
这个就要涉及一些path的存储问题了,前面在path中的定义中说过,Path是封装了由直线和曲线(二次,三次贝塞尔曲线)构成的几何路径。其中曲线部分用的是贝塞尔曲线,稍后再讲。 然而除了曲线部分就只剩下直线了,对于直线的存储最简单的就是记录坐标点,然后直接连接各个点就行了。虽然记录矩形只需要两个点,但是如果只用两个点来记录一个矩形的话,就要额外增加一个标志位来记录这是一个矩形,显然对于存储和解析都是很不划算的事情,将矩形转换为直线,为的就是存储记录方便。
扯了这么多,该回归正题了,就是我们的顺时针和逆时针在这里是干啥的?
图形在实际记录中就是记录各个的点,对于一个图形来说肯定有多个点,既然有这么多的点,肯定就需要一个先后顺序,这里顺时针和逆时针就是用来确定记录这些点的顺序的。
对于上面这个矩形来说,我们采用的是顺时针(CW),所以记录的点的顺序就是 A -> B -> C -> D. 最后一个点就是D,我们这里使用setLastPoint改变最后一个点的位置实际上是改变了D的位置。
理解了上面的原理之后,设想如果我们将顺时针改为逆时针(CCW),则记录点的顺序应该就是 A -> D -> C -> B, 再使用setLastPoint则改变的是B的位置,我们试试看结果和我们的猜想是否一致:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 Path path = new Path(); path.addRect(-200,-200,200,200, Path.Direction.CCW); path.setLastPoint(-300,300); // <-- 重置最后一个点的位置 canvas.drawPath(path,mPaint);

通过验证发现,发现结果和我们猜想的一样,但是还有一个潜藏的问题不晓得大家可否注意到。我们用两个点的坐标确定了一个矩形,矩形起始点(A)就是我们指定的第一个点的坐标。
需要注意的是,交换坐标点的顺序可能就会影响到某些绘制内容哦,例如上面的例子,你可以尝试交换两个坐标点,或者指定另外两个点来作为参数,虽然指定的是同一个矩形,但实际绘制出来是不同的哦。
参数中点的顺序很重要!
参数中点的顺序很重要!
参数中点的顺序很重要!
重要的话说三遍,本次是用矩形作为例子的,其他的几个图形基本上都包含了曲线,详情参见后续的贝塞尔曲线部分。
关于顺时针和逆时针对图形填充结果的影响请参考 Path之完结篇,虽然只讲了一个Path,但也是内容颇多,放进一篇中就太长了,请见谅。
第二类(Path)
方法预览:
// 第二类(Path) // path public void addPath(Pathsrc) public void addPath(Pathsrc,floatdx,floatdy) public void addPath(Pathsrc,Matrixmatrix)
这个相对比较简单,也很容易理解,就是将两个Path合并成为一个。
第三个方法是将src添加到当前path之前先使用Matrix进行变换。
第二个方法比第一个方法多出来的两个参数是将src进行了位移之后再添加进当前path中。
示例:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心
canvas.scale(1,-1); // <-- 注意 翻转y坐标轴
Path path = new Path();
Path src = new Path();
path.addRect(-200,-200,200,200, Path.Direction.CW);
src.addCircle(0,0,100, Path.Direction.CW);
path.addPath(src,0,200);
mPaint.setColor(Color.BLACK); // 绘制合并后的路径
canvas.drawPath(path,mPaint);
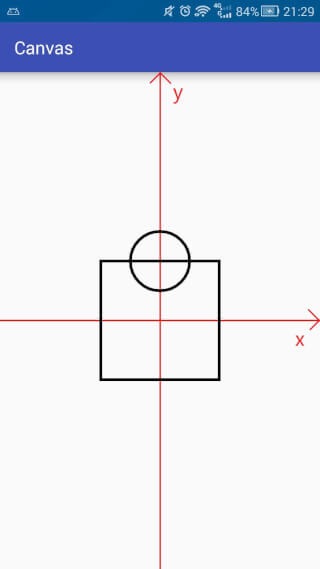
首先我们新建地方两个Path(矩形和圆形)中心都是坐标原点,我们在将包含圆形的path添加到包含矩形的path之前将其进行移动了一段距离,最终绘制出来的效果就如上面所示。
第三类(addArc与arcTo)
方法预览:
// 第三类(addArc与arcTo) // addArc public void addArc(RectFoval,floatstartAngle,floatsweepAngle)// arcTo public void arcTo(RectFoval,floatstartAngle,floatsweepAngle) public void arcTo(RectFoval,floatstartAngle,floatsweepAngle,booleanforceMoveTo)
参数表:
| 参数 | 摘要 |
|---|---|
| oval | 圆弧的外切矩形。 |
| startAngle | 开始角度 |
| sweepAngle | 扫过角度(-360 <= sweepAngle <360) |
| forceMoveTo | 是否强制使用MoveTo |
PS: sweepAngle取值范围是 [-360, 360),不包括360,当 >= 360 或者 < -360 时将不会绘制任何内容, 对于360,你可以用一个接近的值替代,例如: 359.99。
从名字就可以看出,这两个方法都是与圆弧相关的,作用都是添加一个圆弧到path中,但既然存在两个方法,两者之间肯定是有区别的:
| 名称 | 作用 | 区别 |
|---|---|---|
| addArc | 添加一个圆弧到path | 直接添加一个圆弧到path中 |
| arcTo | 添加一个圆弧到path | 添加一个圆弧到path,如果圆弧的起点和上次最后一个坐标点不相同,就连接两个点 |
可以看到addArc有1个方法(实际上是两个的,但另一个重载方法是API21添加的), 而arcTo有2个方法,其中一个最后多了一个布尔类型的变量forceMoveTo。
forceMoveTo是什么作用呢?
这个变量意思为“是否强制使用moveTo”,也就是说,是否使用moveTo将变量移动到圆弧的起点位移,也就意味着:
| forceMoveTo | 含义 | 等价方法 |
|---|---|---|
| true | 将最后一个点移动到圆弧起点,即不连接最后一个点与圆弧起点 | public void addArc (RectF oval, float startAngle, float sweepAngle) |
| false | 不移动,而是连接最后一个点与圆弧起点 | public void arcTo (RectF oval, float startAngle, float sweepAngle) |
示例(addArc):
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 canvas.scale(1,-1); // <-- 注意 翻转y坐标轴 Path path = new Path(); path.lineTo(100,100); RectF oval = new RectF(0,0,300,300); path.addArc(oval,0,270); // path.arcTo(oval,0,270,true); // <-- 和上面一句作用等价 canvas.drawPath(path,mPaint);
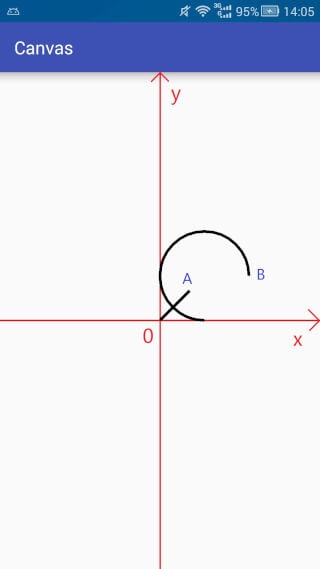
示例(arcTo):
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心
canvas.scale(1,-1); // <-- 注意 翻转y坐标轴
Path path = new Path();
path.lineTo(100,100);
RectF oval = new RectF(0,0,300,300);
path.arcTo(oval,0,270);
// path.arcTo(oval,0,270,false); // <-- 和上面一句作用等价
canvas.drawPath(path,mPaint);
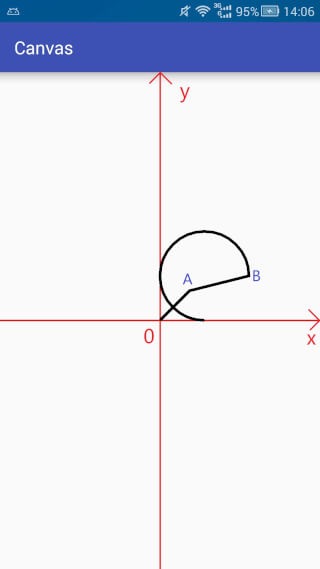
从上面两张运行效果图可以清晰的看出来两者的区别,我就不再废话了。
第3组:isEmpty、 isRect、isConvex、 set 和 offset
这一组比较简单,稍微说一下就可以了。
isEmpty
方法预览:
public boolean isEmpty()
判断path中是否包含内容。
Path path = new Path(); Log.e("1",path.isEmpty()+""); path.lineTo(100,100); Log.e("2",path.isEmpty()+"");
log输出结果:
com.sloop.canvas E/1: true com.sloop.canvas E/2: false
isRect
方法预览:
public boolean isRect(RectFrect)
判断path是否是一个矩形,如果是一个矩形的话,会将矩形的信息存放进参数rect中。
path.lineTo(0,400); path.lineTo(400,400); path.lineTo(400,0); path.lineTo(0,0); RectF rect = new RectF(); boolean b = path.isRect(rect); Log.e("Rect","isRect:"+b+"| left:"+rect.left+"| top:"+rect.top+"| right:"+rect.right+"| bottom:"+rect.bottom);
log 输出结果:
com.sloop.canvas E/Rect: isRect:true| left:0.0| top:0.0| right:400.0| bottom:400.0
set
方法预览:
public void set(Pathsrc)
将新的path赋值到现有path。
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 canvas.scale(1,-1); // <-- 注意 翻转y坐标轴 Path path = new Path(); // path添加一个矩形 path.addRect(-200,-200,200,200, Path.Direction.CW); Path src = new Path(); // src添加一个圆 src.addCircle(0,0,100, Path.Direction.CW); path.set(src); // 大致相当于 path = src; canvas.drawPath(path,mPaint);
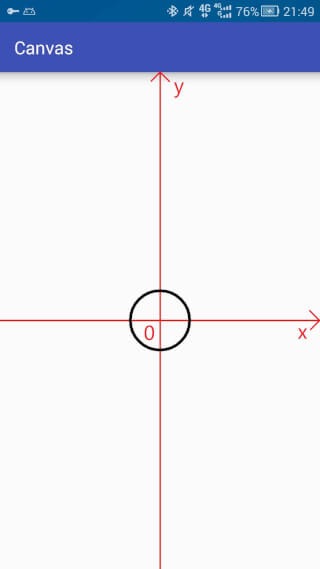
offset
方法预览:
public void offset(floatdx,floatdy) public void offset(floatdx,floatdy,Pathdst)
这个的作用也很简单,就是对path进行一段平移,它和Canvas中的translate作用很像,但Canvas作用于整个画布,而path的offset只作用于当前path。
但是第二个方法最后怎么会有一个path作为参数?
其实第二个方法中最后的参数das是存储平移后的path的。
| dst状态 | 效果 |
|---|---|
| dst不为空 | 将当前path平移后的状态存入dst中,不会影响当前path |
| dat为空(null) | 平移将作用于当前path,相当于第一种方法 |
示例:
canvas.translate(mWidth / 2, mHeight / 2); // 移动坐标系到屏幕中心 canvas.scale(1,-1); // <-- 注意 翻转y坐标轴 Path path = new Path(); // path中添加一个圆形(圆心在坐标原点) path.addCircle(0,0,100, Path.Direction.CW); Path dst = new Path(); // dst中添加一个矩形 dst.addRect(-200,-200,200,200, Path.Direction.CW); path.offset(300,0,dst); // 平移 canvas.drawPath(path,mPaint); // 绘制path mPaint.setColor(Color.BLUE); // 更改画笔颜色 canvas.drawPath(dst,mPaint); // 绘制dst

从运行效果图可以看出,虽然我们在dst中添加了一个矩形,但是并没有表现出来,所以,当dst中存在内容时,dst中原有的内容会被清空,而存放平移后的path。
三.总结
本想一篇把path写完,但是万万没想到居然扯了这么多。本篇中讲解的是直线部分和一些常用方法,下一篇将着重讲解贝塞尔曲线和自相交图形渲染等相关问题,敬请期待哦。
学完本篇之后又解锁了新的境界,可以看看这位大神的文章 Android雷达图(蜘蛛网图)绘制
这个精小干练,非常适合新手练习使用,帮助大家更好的熟悉path的使用。