Java8中的HashMap分析

本篇文章是网上多篇文章的精华的总结，结合自己看源代码的一些感悟，其中线程安全性和性能测试部分并未做实践测试，直接是“拿来”网上的博客的。

哈希表概述

哈希表本质上一个数组，数组中每一个元素称为一个箱子（Bin），箱子中存放的是键值对Entry<K,V>链表，因而也称之为链表散列。

我们可以用图来形象地说明这个结构：

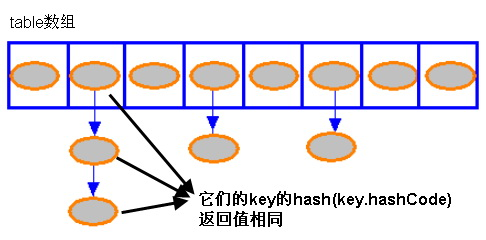
哈希表是如何工作的？

存储

Step1：根据哈希函数来计算HashCode值h，其中键值对Entry<K,V>的K来计算时需要的参数。

Step2：根据HashCode，来计算存放在哈希表（长度为n）中的位置（箱子的位置），一种计算方法是取余：h%n。

Step3：如果该箱子中已经存在键值对数据，则使用开放寻址法或拉链法解决冲突。

获取

Step1：根据key值计算HashCode的值h。

Step2：假设箱子的个数为 n，那么这个键值对应该放在第 (h % n) 个箱子中。

Step3：如果这个箱子里有多个键值对，同时假设箱子里的多个值是采用链表的方式存储，则需要遍历这个链表，复杂度为O(n)。

扩容

哈希表还有 一个重要的属性：负载因子，它是衡量哈希表的空/满程度，一定程度上也能体现查询的效率。其计算公式为：

负载因子 = 总键值对数 / 箱子数量

负载因子越大，意味着哈希表越满，越容易导致冲突（更大的概念找到同一个箱子上），因而查询效率也就更低。因而，一般来说，当负载因子大于某个常数（可能是1，也可能是其他值，Java8的HashMap的负载因子为0.75）时，哈希表就会自动扩容。

哈希表在扩容的时候，一般都会选择扩大2的倍数，同时将原来的哈希表的数据迁移到新的哈希表中，这样即使key的哈希值不变，对箱子的取余结果（假设我们用这种方法来计算HashCode）也会不同，因此所有的箱子和元素的存放位置都有可能发生变化，这个过程也称为重哈希（rehash）。

哈表的扩容并不能有效解决负载因子过大的问题，因为在前面的取HashCode的方法中，假设所有key的HashCode值都一样，那么即使扩容以后他们在哈希表中的位置也不会变，实际存放在箱子中的链表长度也不变，因此也就不能提高哈希表的查询速度。

因而，哈希表存在以下两个问题：

 1、在扩容的时候，重哈希的成本比较大

 2、如果Hash函数设计地不合理（如上面举例说明的取余），会导致哈希表中极端情况下变成线性表，性能极低。

我们下面来看看Java8中是如何处理这两个问题的。

以上这部分内容多参考自：深入理解哈希表 ，图片来自于HashMap的图示

Java8中的HashMap

在说明这个问题之前，我们来看下HashMap在Java8中在类图关系，如下所示：

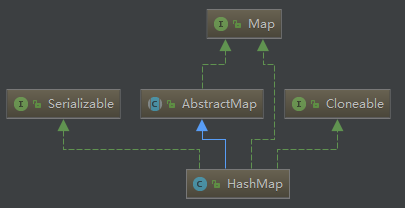
Java8中通过如下几种方式来解决上面的两个问题：

一、让元素分布地更合理

      （下面这部分不知道是哪位大神写的，原文照抄吧）

      学过概率论的读者也许知道，理想状态下哈希表的每个箱子中，元素的数量遵守泊松分布：

      

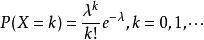
      当负载因子为 0.75 时，上述公式中 λ 约等于 0.5，因此箱子中元素个数和概率的关系如下：

      

数量	概率
0	0.60653066
1	0.30326533
2	0.07581633
3	0.01263606
4	0.00157952
5	0.00015795
6	0.00001316
7	0.00000094
8	0.00000006

      这就是为什么我们将0.75设为负载因子，同时针对箱子中链表长度超过8以后要做另外的优化（一来是优化的概念较小，二来是优化过后的效率提升明显）。所以，一般情况下负载因子不建议修改；同时如果在数量为8的链表的概率较大，则几乎可以认为是哈希函数设计有问题导致的。

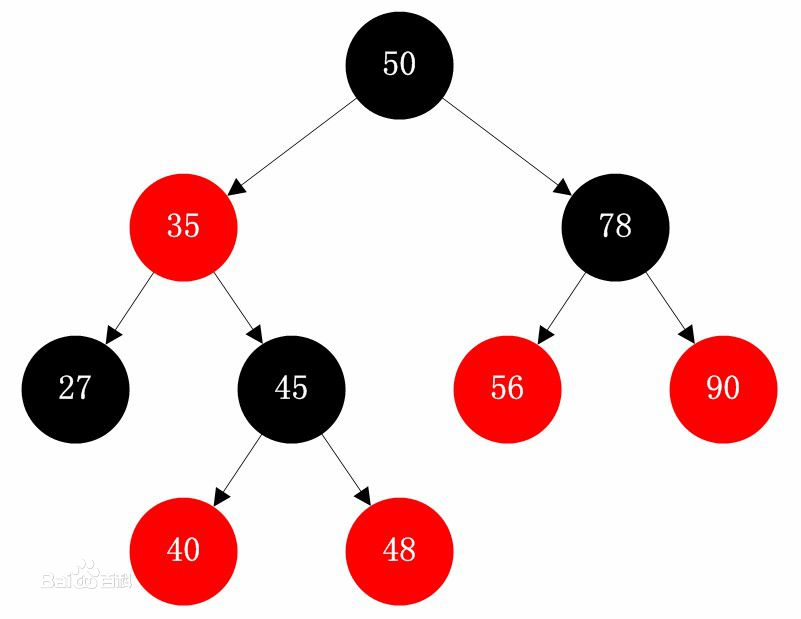
二、通过红黑树让查询更有效率（O(n)—>O(Log(n))）

       第一点已经说明，当箱子中的链表元素超过8个时，会将这个链表转为红黑树，红黑树的查找效率为O(log(n))。红黑树的示图如下：

      

三、让扩容时重哈希(rehash)的成本变得更小

       在Java7中，重哈希是要重新计算Hash值的，而在Java8中，通过高位运算的巧妙设计，避免了这种计算。下面我们举例说明：

      我们要在初始大小为2的HashMap中存储3、5、7这3个值，Hash函数为取余法。

      Step1：在开始的时候，3、5、7经过Hash过后 3%2=1、5%2=1、7%2=1，因而3、5、7存储在同一个箱子的链表中（地址为1）。

      Step2：现在扩容了，扩容后的大小为2*2=4，现在经过Hash后3%4=3、5%4=1、7%4=3，因而3与7一起放在箱子的链表中（地址为3），5单独存放在一个箱子里（地址为1）。

      整个过程如下图所示：

      

      我们注意到，在扩容后3和7的位置变化了，由1—>3（=1+2）

      再进行扩容，由4容为8，那么经过Hash后，3%8=3、5%8=5、7%8=7，分别存放于3、5（=1+4）、7（=3+4）这几个位置中。

      我们发现，扩容后的元素要么在原位置，要么在原位置再移动2次幂的位置，整个过程只需要使用一个位运算符<<就可以了（在源码的resize方法中可以找到）。

      我们用计算机的地址来展示这个过程：

      

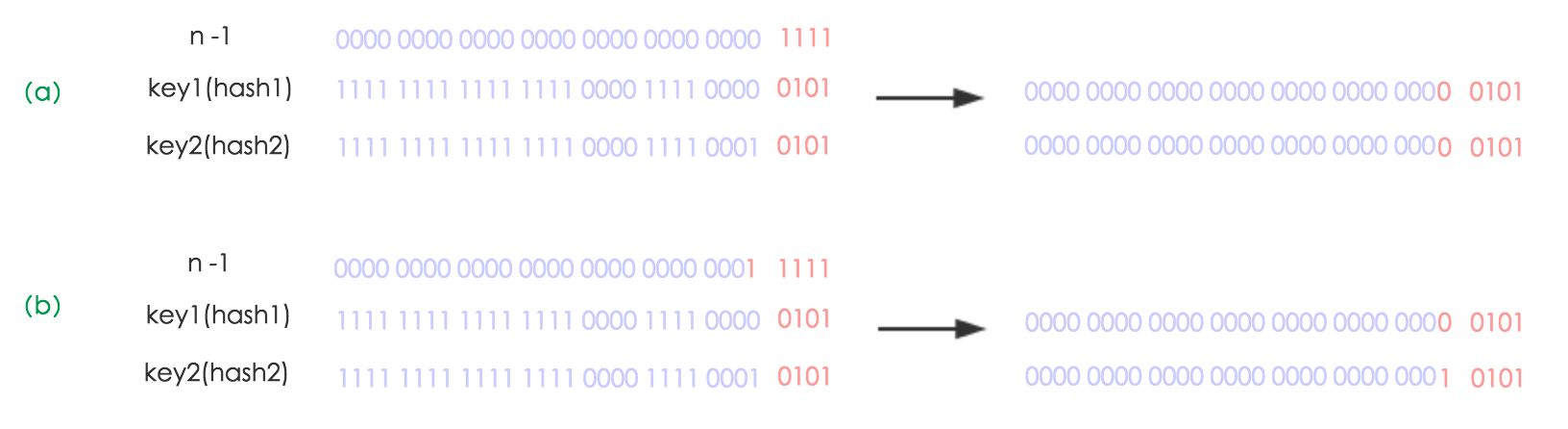
      n为table的长度，图（a）表示扩容前的key1和key2两种key确定索引位置的示例，图（b）表示扩容后key1和key2两种key确定索引位置的示例，其中hash1是key1对应的哈希与高位运算结果。元素在重新计算hash之后，因为n变为2倍，那么n-1的mask范围在高位多1bit(红色)，因此新的index就会发生这样的变化：

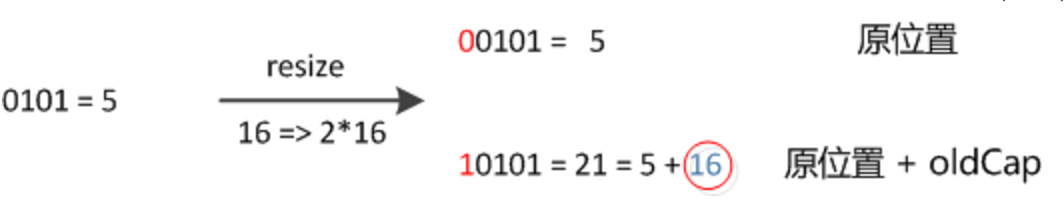
      因此，我们在扩充HashMap的时候，不需要像JDK1.7的实现那样重新计算hash，只需要看看原来的hash值新增的那个bit是1还是0就好了，是0的话索引没变，是1的话索引变成“原索引+oldCap”，可以看看下图为16扩充为32的resize示意图：

     

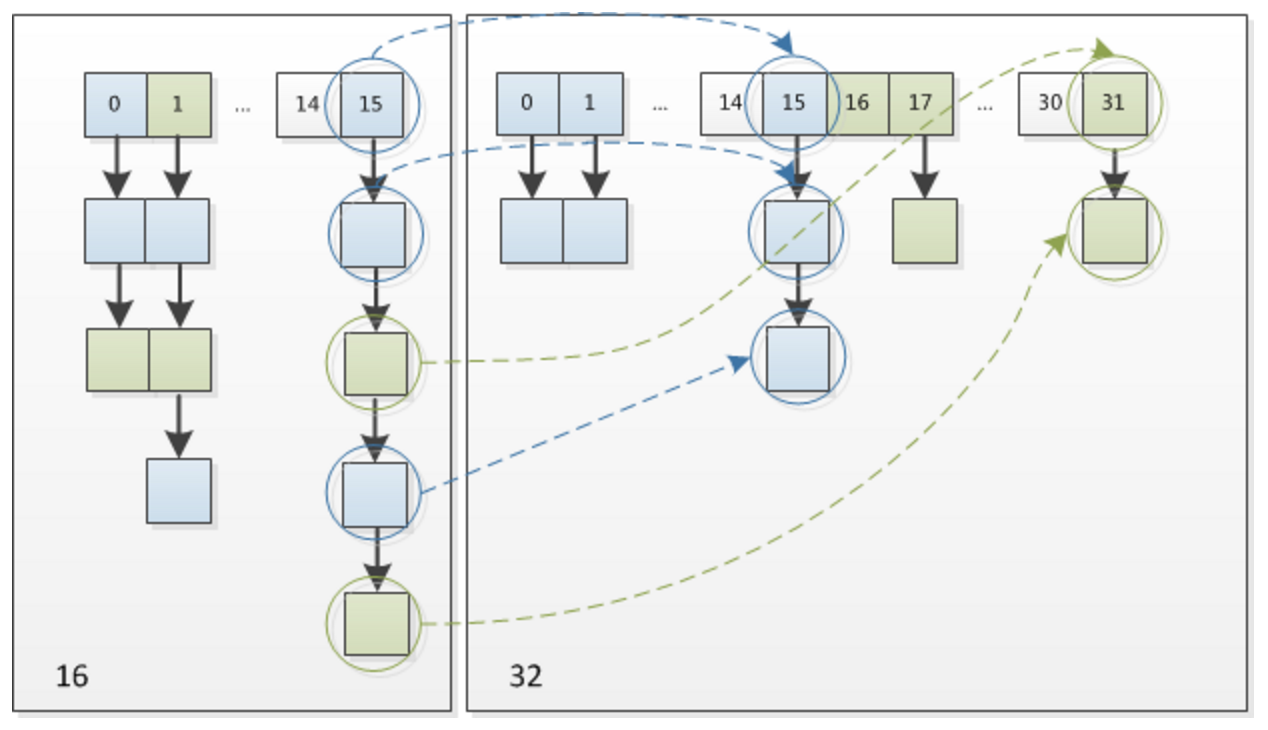
      这个设计确实非常的巧妙，既省去了重新计算hash值的时间，而且同时，由于新增的1bit是0还是1可以认为是随机的，因此resize的过程，均匀的把之前的冲突的节点分散到新的bucket了。这一块就是JDK1.8新增的优化点。

      以上这部分中的图示和位移讲解的内容参考自：深入分析hashmap

另外：

四：我们可以通过适当地初始化大小来控制扩容的次数：既然扩容是不可避免的，我们就尽可能少地让它发生，要实际编程的时候，应该根据业务合理地设置初始大小的值。

此外，Java8中HashMap还提供了另外一些参数来控制HashMap的性能，如下所示：

    /**
     * 默认的初始化大小(必须为2的幂)
     */
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

    /**
     * 最大的存储数量(默认的数量,可以在构造函数中指定)
     * 必须为2的幂同时小于2的30次方
     */
    static final int MAXIMUM_CAPACITY = 1 << 30;

    /**
     * 默认的负载因子,可以在构建函数中指定
     */
    static final float DEFAULT_LOAD_FACTOR = 0.75f;

    /**
     * HashMap由链表转为红黑树存储的阀值
     * 1.8提供的新特性
     */
    static final int TREEIFY_THRESHOLD = 8;

    /**
     * HashMap由红黑树转为链表存储的阀值
     */
    static final int UNTREEIFY_THRESHOLD = 6;

    /**
     * HashMap的箱子中的链表转为红黑树之前还有一个判断:
     * 只在所有箱子(键值对)的数量大于64才会发生转换
     * 这样是为了避免在哈希表建立初期,多个键值对恰好被放入了同一个链表而导致不必要的转化
     */
    static final int MIN_TREEIFY_CAPACITY = 64;

源码中的关键方法

 方法一、hash方法

static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);//这里其实就要求大家来重写HashCode方法
    }

 方法二、putVal方法

下面是putVal方法的执行过程图示：

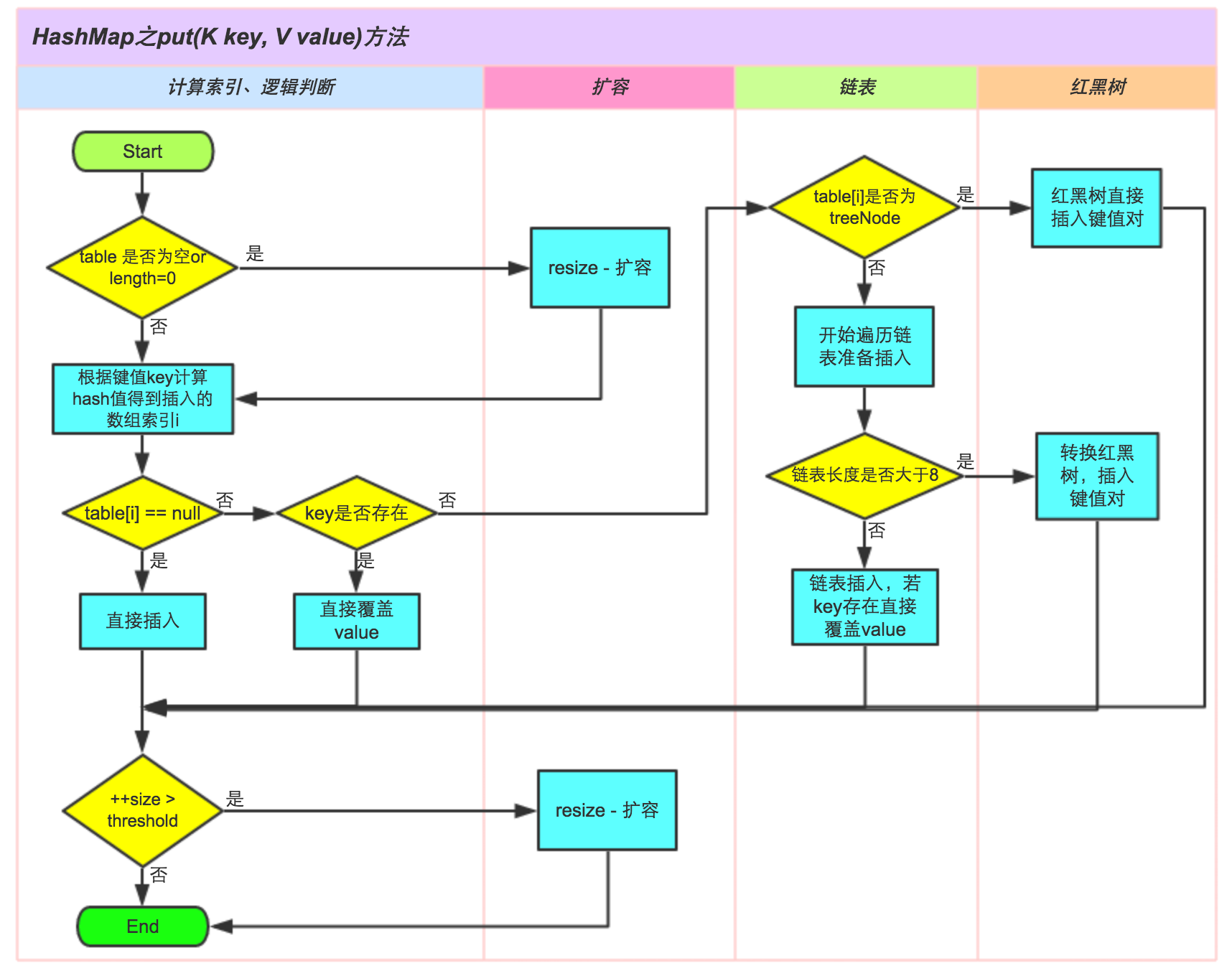
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                boolean evict) {
     Node<K,V>[] tab; Node<K,V> p; int n, i;
     // 步骤①：tab为空则创建
     if ((tab = table) == null || (n = tab.length) == 0)
         n = (tab = resize()).length;
     // 步骤②：计算index，并对null做处理
     if ((p = tab[i = (n - 1) & hash]) == null)
         tab[i] = newNode(hash, key, value, null);
     else {
         Node<K,V> e; K k;
         // 步骤③：节点key存在，直接覆盖value
         if (p.hash == hash &&
             ((k = p.key) == key || (key != null && key.equals(k))))
             e = p;
         // 步骤④：判断该链为红黑树
         else if (p instanceof TreeNode)
             e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        // 步骤⑤：该链为链表
         else {
             for (int binCount = 0; ; ++binCount) {
                 if ((e = p.next) == null) {
                     p.next = newNode(hash, key,value,null);
                        //链表长度大于8转换为红黑树进行处理
                     if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st 
                         treeifyBin(tab, hash);
                     break;
                 }
                    // key已经存在直接覆盖value
                 if (e.hash == hash &&
                     ((k = e.key) == key || (key != null && key.equals(k))))
                            break;
                 p = e;
             }
         }
        
         if (e != null) { // existing mapping for key
             V oldValue = e.value;
             if (!onlyIfAbsent || oldValue == null)
                 e.value = value;
             afterNodeAccess(e);
             return oldValue;
         }
     }
     ++modCount;
     // 步骤⑥：超过最大容量 就扩容
     if (++size > threshold)
         resize();
     afterNodeInsertion(evict);
     return null;
 }

 

      这个 getNode() 方法就是根据哈希表元素个数与哈希值求模（使用的公式是 (n - 1) &hash）得到 key 所在的桶的头结点，如果头节点恰好是红黑树节点，就调用红黑树节点的 getTreeNode() 方法，否则就遍历链表节点。

 

 方法三、节点查找方法getNode 

final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
       if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        if ((e = first.next) != null) {
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
               if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    return null;
}

   

方法四、红黑树生成方法

//将桶内所有的 链表节点 替换成 红黑树节点

final void treeifyBin(Node<K,V>[] tab, int hash) {

    int n, index; Node<K,V> e;

    //如果当前哈希表为空，或者哈希表中元素的个数小于 进行树形化的阈值(默认为 64)，就去新建/扩容

   if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)

        resize();

    else if ((e = tab[index = (n - 1) & hash]) != null) {

        //如果哈希表中的元素个数超过了 树形化阈值，进行树形化

        // e 是哈希表中指定位置桶里的链表节点，从第一个开始

        TreeNode<K,V> hd = null, tl = null; //红黑树的头、尾节点

        do {

            //新建一个树形节点，内容和当前链表节点 e 一致

            TreeNode<K,V> p = replacementTreeNode(e, null);

            if (tl == null) //确定树头节点

                hd = p;

           else {

               p.prev = tl;

                tl.next = p;

            }

            tl = p;

        } while ((e = e.next) != null); 

        //让桶的第一个元素指向新建的红黑树头结点，以后这个桶里的元素就是红黑树而不是链表了

        if ((tab[index] = hd) != null)

            hd.treeify(tab);

    }

 }

    TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {

    return new TreeNode<>(p.hash, p.key, p.value, next);

 }

  

方法五、红黑树节点查找方法

final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
            TreeNode<K,V> p = this;
            do {
                int ph, dir; K pk;
                TreeNode<K,V> pl = p.left, pr = p.right, q;
                if ((ph = p.hash) > h)
                    p = pl;
                else if (ph < h)
                    p = pr;
                else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                    return p;
                else if (pl == null)
                    p = pr;
                else if (pr == null)
                    p = pl;
                else if ((kc != null ||
                          (kc = comparableClassFor(k)) != null) &&
                         (dir = compareComparables(kc, k, pk)) != 0)
                    p = (dir < 0) ? pl : pr;
                else if ((q = pr.find(h, k, kc)) != null)
                    return q;
                else
                    p = pl;
            } while (p != null);
            return null;
        }

  

方法六、扩容方法

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        // 超过最大值就不再扩充了，就只好随你碰撞去吧
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        // 没超过最大值，就扩充为原来的2倍
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    // 计算新的resize上限
    if (newThr == 0) {

        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
        Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        // 把每个bucket都移动到新的buckets中
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode)
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { // preserve order
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        // 原索引
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        // 原索引+oldCap
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    // 原索引放到bucket里
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    // 原索引+oldCap放到bucket里
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

  

方法七、扩容后的元素转移方法

 void transfer(Entry[] newTable) {
     Entry[] src = table;                   //src引用了旧的Entry数组
     int newCapacity = newTable.length;
     for (int j = 0; j < src.length; j++) { //遍历旧的Entry数组
         Entry<K,V> e = src[j];             //取得旧Entry数组的每个元素
         if (e != null) {
             src[j] = null;//释放旧Entry数组的对象引用（for循环后，旧的Entry数组不再引用任何对象）
             do {
                 Entry<K,V> next = e.next;
                 int i = indexFor(e.hash, newCapacity); //！！重新计算每个元素在数组中的位置
                 e.next = newTable[i]; //标记[1]
                 newTable[i] = e;      //将元素放在数组上
                 e = next;             //访问下一个Entry链上的元素
             } while (e != null);
         }
     }
17 }

 

线程安全性

在多线程使用场景中，应该尽量避免使用线程不安全的HashMap，而使用线程安全的ConcurrentHashMap。那么为什么说HashMap是线程不安全的，下面举例子说明在并发的多线程使用场景中使用HashMap可能造成死循环。代码例子如下(便于理解，仍然使用JDK1.7的环境)： 

public class HashMapInfiniteLoop {  
 
    private static HashMap<Integer,String> map = new HashMap<Integer,String>(2，0.75f);  
    public static void main(String[] args) {  
        map.put(5， "C");  
 
        new Thread("Thread1") {  
            public void run() {  
                map.put(7, "B");  
                System.out.println(map);  
            };  
        }.start();  
        new Thread("Thread2") {  
            public void run() {  
                map.put(3, "A);  
                System.out.println(map);  
            };  
        }.start();        
    }  
}

其中，map初始化为一个长度为2的数组，loadFactor=0.75，threshold=2*0.75=1，也就是说当put第二个key的时候，map就需要进行resize。

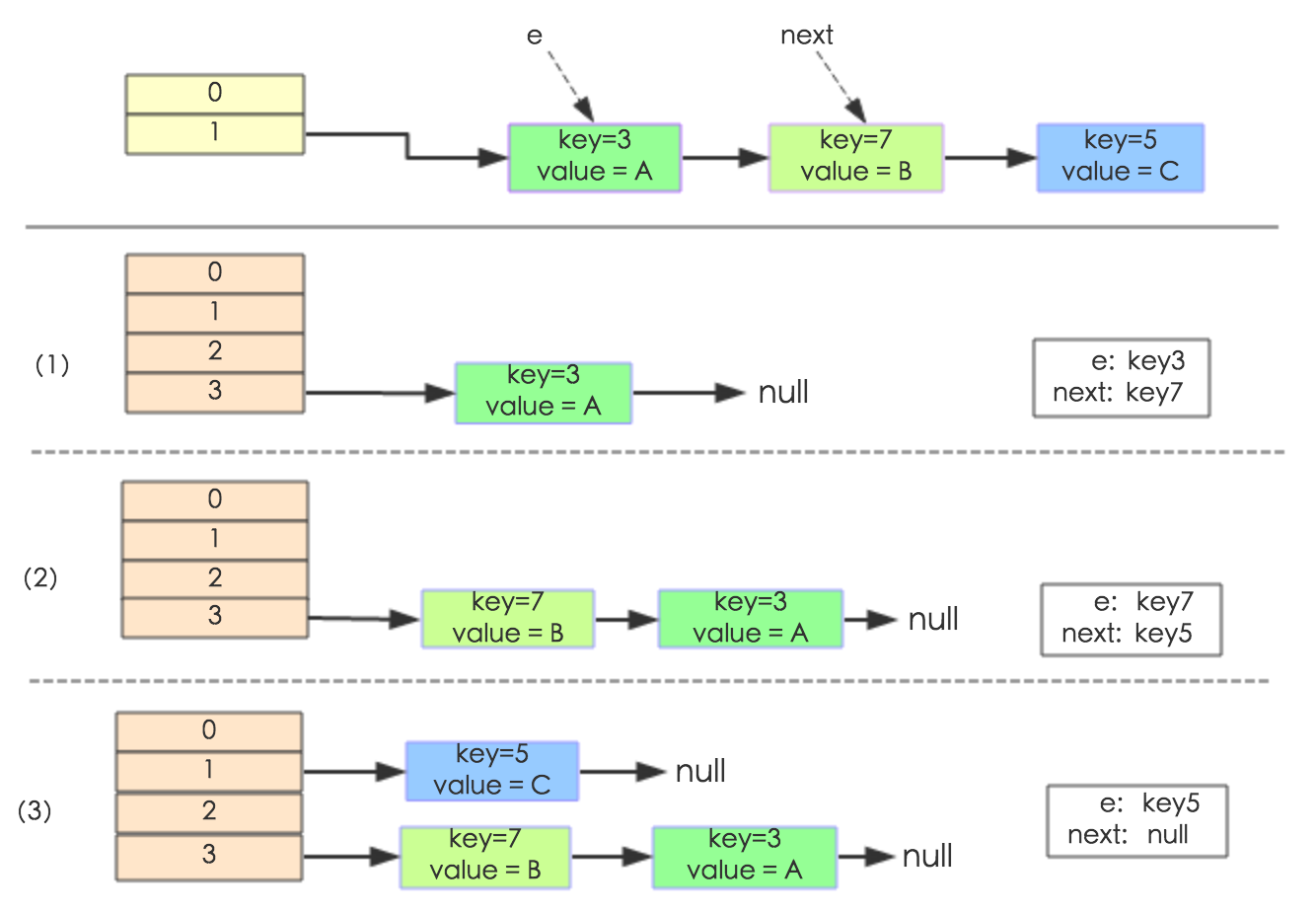
通过设置断点让线程1和线程2同时debug到transfer方法(3.3小节代码块)的首行。注意此时两个线程已经成功添加数据。放开thread1的断点至transfer方法的“Entry next = e.next;” 这一行；然后放开线程2的的断点，让线程2进行resize。结果如下图：

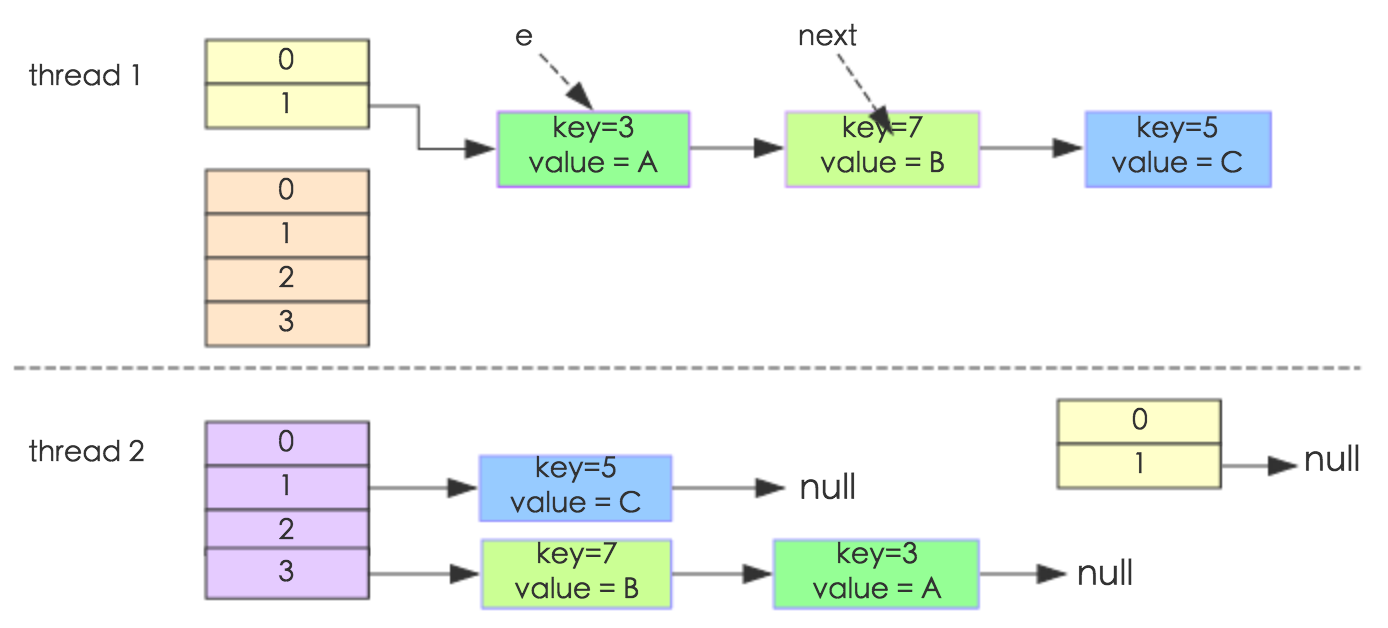
注意，Thread1的 e 指向了key(3)，而next指向了key(7)，其在线程二rehash后，指向了线程二重组后的链表。

线程一被调度回来执行，先是执行 newTalbe[i] = e， 然后是e = next，导致了e指向了key(7)，而下一次循环的next = e.next导致了next指向了key(3)。

e.next = newTable[i] 导致 key(3).next 指向了 key(7)。注意：此时的key(7).next 已经指向了key(3)， 环形链表就这样出现了。

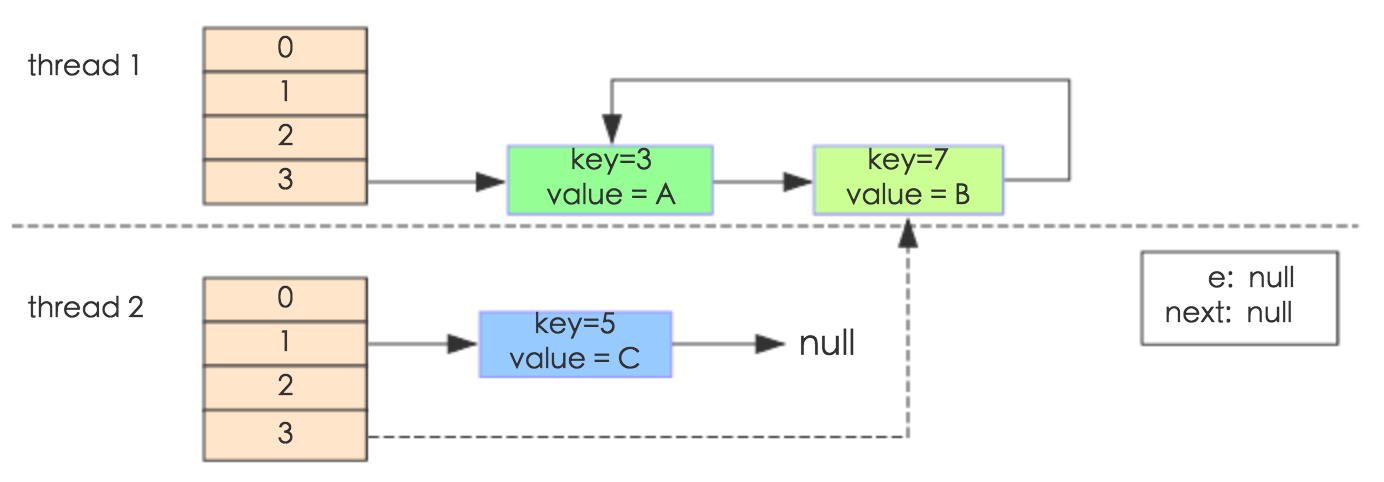
于是，当我们用线程一调用map.get(11)时，悲剧就出现了——Infinite Loop。

性能表现：JDK1.8 vs JDK1.7

HashMap中，如果key经过hash算法得出的数组索引位置全部不相同，即Hash算法非常好，那样的话，getKey方法的时间复杂度就是O(1)，如果Hash算法技术的结果碰撞非常多，假如Hash算极其差，所有的Hash算法结果得出的索引位置一样，那样所有的键值对都集中到一个桶中，或者在一个链表中，或者在一个红黑树中，时间复杂度分别为O(n)和O(lgn)。 鉴于JDK1.8做了多方面的优化，总体性能优于JDK1.7，下面我们从两个方面用例子证明这一点。

Hash较均匀的情况

为了便于测试，我们先写一个类Key，如下：

class Key implements Comparable<Key> {
 
    private final int value;
 
    Key(int value) {
        this.value = value;
    }
 
    @Override
    public int compareTo(Key o) {
        return Integer.compare(this.value, o.value);
    }
 
    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass())
            return false;
        Key key = (Key) o;
        return value == key.value;
    }
 
    @Override
    public int hashCode() {
        return value;
    }
}

这个类复写了equals方法，并且提供了相当好的hashCode函数，任何一个值的hashCode都不会相同，因为直接使用value当做hashcode。为了避免频繁的GC，我将不变的Key实例缓存了起来，而不是一遍一遍的创建它们。代码如下：

public class Keys {
 
    public static final int MAX_KEY = 10_000_000;
    private static final Key[] KEYS_CACHE = new Key[MAX_KEY];
 
    static {
        for (int i = 0; i < MAX_KEY; ++i) {
            KEYS_CACHE[i] = new Key(i);
        }
    }
 
    public static Key of(int value) {
        return KEYS_CACHE[value];
    }
}

现在开始我们的试验，测试需要做的仅仅是，创建不同size的HashMap（1、10、100、……10000000），屏蔽了扩容的情况，代码如下：

static void test(int mapSize) {
 
       HashMap<Key, Integer> map = new HashMap<Key,Integer>(mapSize);
       for (int i = 0; i < mapSize; ++i) {
           map.put(Keys.of(i), i);
       }
 
       long beginTime = System.nanoTime(); //获取纳秒
       for (int i = 0; i < mapSize; i++) {
           map.get(Keys.of(i));
       }
       long endTime = System.nanoTime();
       System.out.println(endTime - beginTime);
   }
 
   public static void main(String[] args) {
       for(int i=10;i<= 1000 0000;i*= 10){
           test(i);
       }
   }

在测试中会查找不同的值，然后度量花费的时间，为了计算getKey的平均时间，我们遍历所有的get方法，计算总的时间，除以key的数量，计算一个平均值，主要用来比较，绝对值可能会受很多环境因素的影响。结果如下：

通过观测测试结果可知，JDK1.8的性能要高于JDK1.7 15%以上，在某些size的区域上，甚至高于100%。由于Hash算法较均匀，JDK1.8引入的红黑树效果不明显，下面我们看看Hash不均匀的的情况。

Hash极不均匀的情况

假设我们又一个非常差的Key，它们所有的实例都返回相同的hashCode值。这是使用HashMap最坏的情况。代码修改如下：

class Key implements Comparable<Key> {
 
    //...
 
    @Override
    public int hashCode() {
        return 1;
    }
}

  仍然执行main方法，得出的结果如下表所示：

从表中结果中可知，随着size的变大，JDK1.7的花费时间是增长的趋势，而JDK1.8是明显的降低趋势，并且呈现对数增长稳定。当一个链表太长的时候，HashMap会动态的将它替换成一个红黑树，这话的话会将时间复杂度从O(n)降为O(logn)。hash算法均匀和不均匀所花费的时间明显也不相同，这两种情况的相对比较，可以说明一个好的hash算法的重要性。

小结

1.有两个字典，分别存有 100 条数据和 10000 条数据，如果用一个不存在的 key 去查找数据，在哪个字典中速度更快？

完整的答案是:在 Redis 中，得益于自动扩容和默认哈希函数，两者查找速度一样快。在 Java 和 Objective-C 中，如果哈希函数不合理，返回值过于集中，会导致大字典更慢。Java 由于存在链表和红黑树互换机制，搜索时间呈对数级增长，而非线性增长。在理想的哈希函数下，无论字典多大，搜索速度都是一样快。

2. 扩容是一个特别耗性能的操作，所以当程序员在使用HashMap的时候，估算map的大小，初始化的时候给一个大致的数值，避免map进行频繁的扩容。

3. 负载因子是可以修改的，也可以大于1，但是建议不要轻易修改，除非情况非常特殊。

4. HashMap是线程不安全的，不要在并发的环境中同时操作HashMap，建议使用ConcurrentHashMap。

5. JDK1.8引入红黑树大程度优化了HashMap的性能。

 

参考文档

https://tech.meituan.com/java-hashmap.html

https://www.cnblogs.com/gotodsp/p/6534699.html

https://www.cnblogs.com/shengkejava/p/6771469.html

http://www.importnew.com/14417.html 这篇讲性能的文章值得一看

http://alex09.iteye.com/blog/539545 这是讲Java7中的HashMap的

https://www.cnblogs.com/chinajava/p/5808416.html 这里面讲了Java的HashMap和Redis的HashMap对比

http://blog.csdn.net/Richard_Jason/article/details/53887222

http://www.importnew.com/7099.html