算法学习总结(八)：计数排序

一、算法简介

　　计数排序(Counting sort)是一个非基于比较的稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

二、算法描述

算法的步骤如下：

        1、找出待排序的数组中最大和最小的元素

         2、统计数组中每个值为i的元素出现的次数，存入数组C的第i项

         3、对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）

         4、反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

        当输入的元素是n 个0到k之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

        由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

最差时间复杂度	O(n)
最优时间复杂度	O(n)
平均时间复杂度	O(n)
最差空间复杂度	需要额外辅助空间O(n)

三、算法图解

　　我们使用计数排序对一个乱序的整数数组进行排序。

　　首先创建一个临时数组（长度为输入数据的最大间隔），对于每一个输入数组的整数k，我们在临时数组的第k位置"1"。如下图

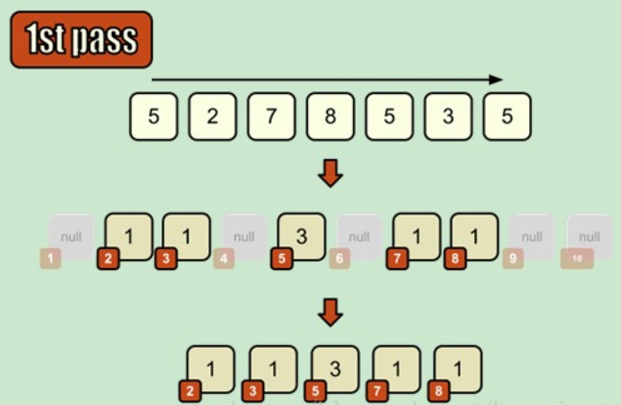
　　上图中，第一行表示输入数据，第二行表示创建的临时数据，临时数组的下标代表输入数据的某一个值，临时数组的值表示输入数据中某一个值的数量。

　　如果输入数据中有重复的数值，那么我们增加临时数组相应的值（比如上图中5有3个，所以小标为5的数组的值是3）。在“初始化”临时数组以后，我们就得到了一个排序好的输入数据。

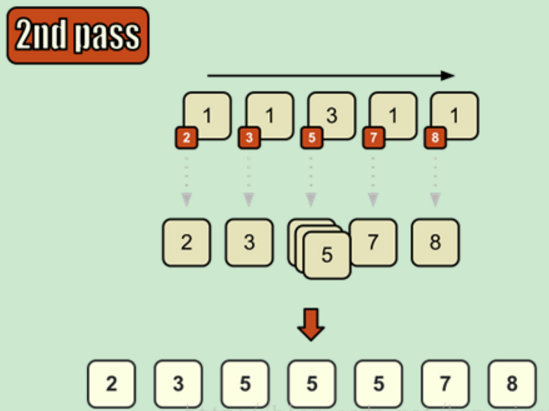　　我们顺序遍历这个数组，将下标解释成数据， 将该位置的值表示该数据的重复数量，记得得到一个排序好的数组。

四、示例代码

public class CountingSort {
    public int[] countingSort(int[] A, int n) {
        count(A);
        return A;
    }

    public static void count(int[] arr) {
        int min = arr[0];
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            min = Math.min(arr[i], min);
            max = Math.max(arr[i], max);
        }
        int[] countArr = new int[max - min + 1];
        for (int i = 0; i < arr.length; i++) {
            countArr[arr[i] - min]++;
        }
        int index = 0;
        for (int i = 0; i < countArr.length; i++) {
            while (countArr[i]-- > 0) {
                arr[index++] = i + min;
            }
        }
    }
}