群

群的性质
- 旋转矩阵集合与旋转乘法构成群
- 变换矩阵与矩阵乘法构成群
- 因此可以称为旋转矩阵群和变换矩阵群
三维旋转矩阵构成了特殊正交群
其他群的例子:
- 一般线性群GL(n) n*n的可逆矩阵 它们对矩阵乘法构成群
- 特殊正交群SO(n)
- 特殊欧式群SE(n)
三维变换矩阵构成了特殊矩阵群
李群与李代数
李群:
- 具有连续(光滑)性质的群
- 既是群也是流形
- 直观上看,一个刚体能连续地在空间中运动,故SO(3)和SE(3)都是李群
- 但是,SO(3)和SE(3)只有定义良好的乘法,没有加法,所以难以进行取极限求导等操作.
李代数:与李群对应的一种结构,位于向量空间.
- 通常记作小写的SO(3)和SE(3),书中以哥特体突出显示.
- 事实上是李群单位元处的正切空间
- 每个李群都有与之对应的李代数。李代数描述了李群单位元附近的正切空间性质
从旋转矩阵引出李代数
- 考虑任意旋转矩阵R,满足 (RR^T=I)

令R随时间变换(连续运动),有(R(t){R(t)}^T=I)
量测对时间求导:(hat{R(t)}{R(t)}^T+R(t){hat{R(t)}}^T=0)
整理:(hat{R(t)=Phi(t)^{ imes}R(t)})
两侧右乘R(t):(hat{R(t)=Phi(t)^{ imes}R(t)})
课看成对R求导之后,左侧多出一个(Phi(t))
单位元附近:(t_0=0),(R(0)=I)
已知初始情况:(R(0)=I),解之,得:
该式说明,对任意t,都可以找到一个R和一个(phi)得对应关系
该关系指指数映射(Exponetial Map)
这里得(phi)称为SO(3)对应得李代数:SO(3)
指数映射与对数映射
指数映射反映了从李代数到李群的对应关系:(R=exp(phi^{wedge}))
问题:但是(phi^{wedge})是一个矩阵,对于矩阵,如何定义求指数运算?
(exp(phi^{wedge})=sum^{}_{n=0} frac{1}{n!}(phi^{wedge})^n)
由于(phi)得向量,定义其角度和模长:
角度乘单位向量:(phi= heta a)
a的性质化解taylor展示中的高阶项提供了有效方法
Taylor展开:
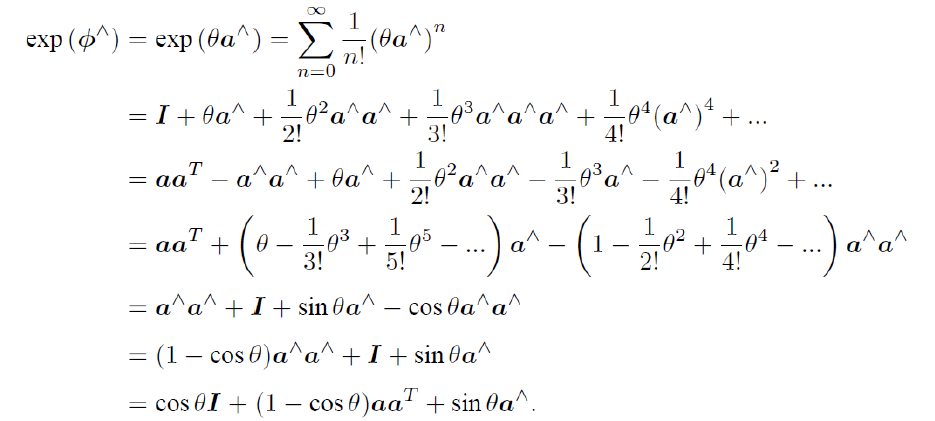
结果:(exp( heta a^{wedge}) = cos heta I+(1-cos heta)aa^T+sin heta a^{wedge})
这说明SO(3)的物理意义就是旋转向量;
反之,给的旋转矩阵是,亦能求李代数:
但实际中没必要这样求,在旋转向量小姐已经介绍了矩阵到向量的转换关系:
$ heta = arccos(frac{tr(R)-1}{2}) $ (Rn=n)
至此,说明了(SO(3))与(so(3))的对应关系。
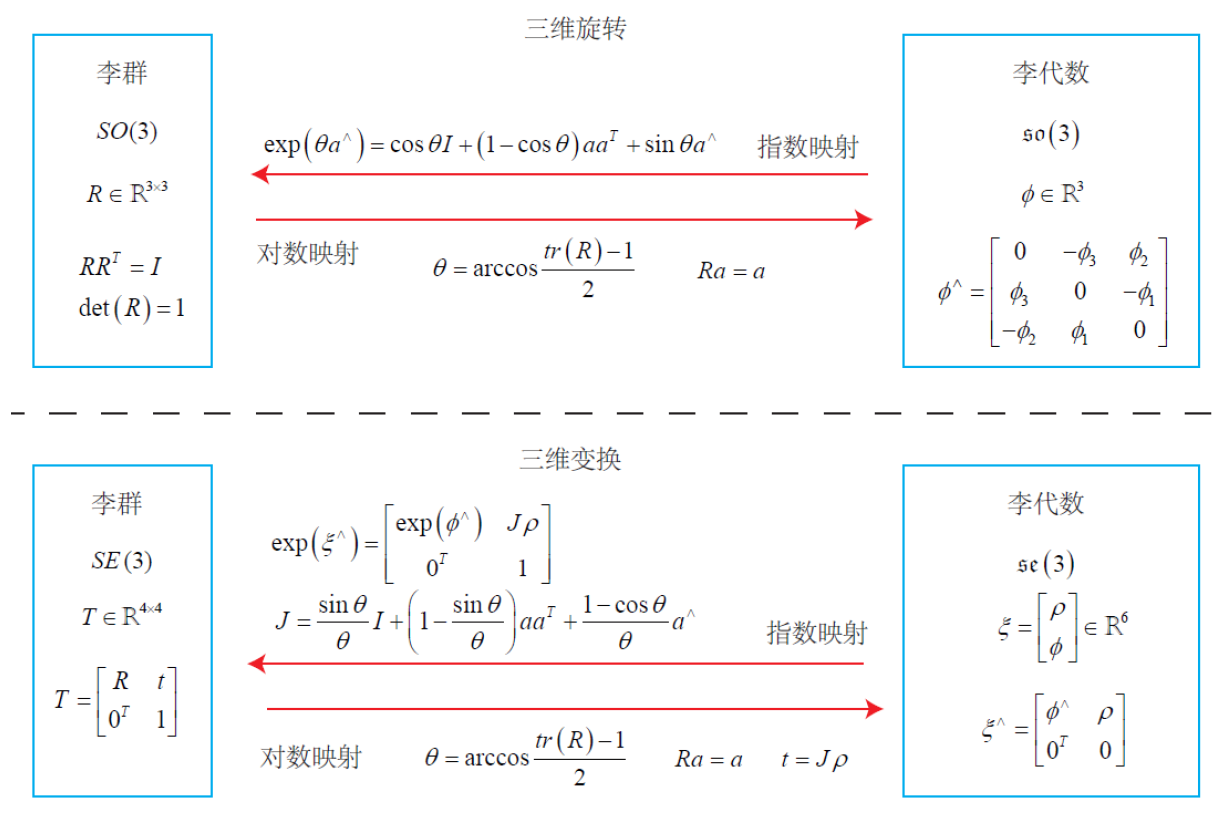
求导与扰动模型
SLAM的定位即位姿估计
但李群无加法:(R_1+R_2
otin SO(3))倒数无从定义
解决方法:
- 利用李代数上加法定义李群元素的导数?
- 使用指数映射和对数映射完成变换关系
基本问题:当在李代数中做加法时,是否等价于在李群上做乘法?
(exp(phi_1^{wedge})exp(phi_2^{vee})=exp((phi_1+phi_2)^{wedge}))
在使用标量的情况下,该式明显成立,但这里的(phi^{wedge})为矩阵,完整形式由BCH公式给出
BCH公式
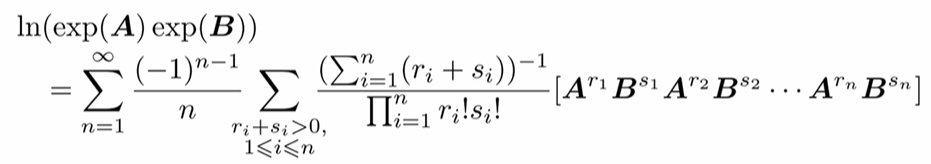
前面的几项:
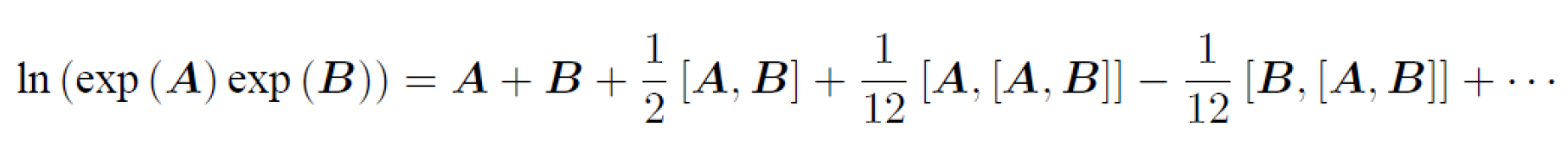


通过 BCH 线性近似,可以定义李代数上的导数
考虑一个基本问题:旋转后的点关于旋转的导数可以不严谨地记为:(frac{partial (Rp)}{partial R})
由于 R 没有加法,导数无从定义,此时存在两种解决办法:
• 对 R 对应的李代数加上小量,求相对于小量的变化率(导数模型);
• 对 R 左乘或右乘一个小量,求相对于小量的李代数的变化率(扰动模型)。
导数模型

扰动模型
左乘一个小量,令其李代数为0

SE(3)上的扰动模型
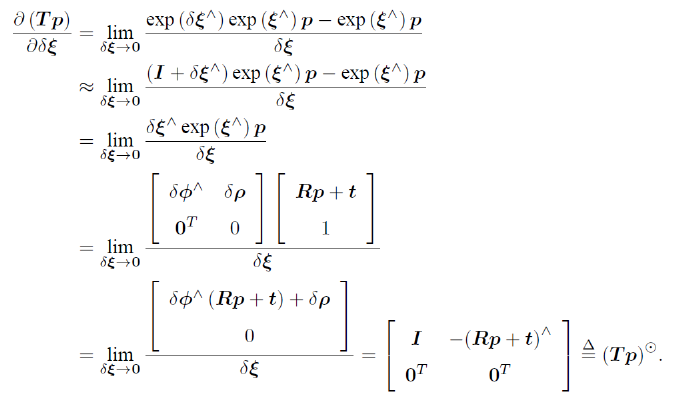
小结
• 利用 BCH 线性近似,可以推导 so(3) 与 se(3) 上的导数和扰动模型
• 通常情况下,扰动模型更为简洁实用
实践:Sophus库
#include "sophus/so3.hpp"
#include "sophus/se3.hpp"