转:http://www.vartang.com/2013/02/吸收马尔可夫链/
在马尔可夫链中,称Pij=1的状态为吸收状态。如果一个马尔可夫链中至少包含一个吸收状态,并且从每一个非吸收状态出发,都可以到达某个吸收状态,那么这个马尔可夫链称为吸收马尔可夫链(Absorbing Markov Chains)[1]。
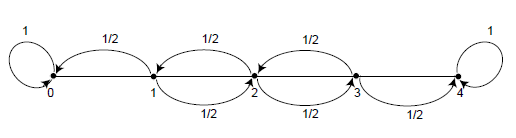
Drunkard's Walk
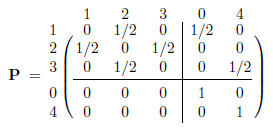
在上图的醉汉游走模型中,当醉汉处于位置1、2或者3时,他将会以等概率(1/2)向左或者向右走,他一直走,直到他到达位置0(他的家)或者位置4(酒吧)才停止游走。这模型的转移矩阵为:

含有r个吸收状态和t个非吸收状态的吸收链,其转移矩阵的标准形式为:
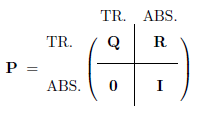
其中,I是一个r×r的单位矩阵,0是一个r×t的零矩阵,R是一个t×r的非零矩阵,Q是一个t×t的矩阵。
吸收链到达吸收状态的概率为1(即当n→∞时,Qn→0)。
对于吸收链P的标准形式,矩阵I-Q具有可逆矩阵N,且N=(I-Q)-1=I+Q+Q2+···。N的元素nij是从非吸收状态si到另一非吸收状态sj的平均转移次数。设c为元素全为1的列向量c=[1,1,···,1]',则t=Nc的第i个分量是从第i个非吸收态出发,到某个吸收状态的平均转移次数。从非吸收状态i出发终被吸收状态j吸收的概率由B=NR给出。
以上图的醉汉游走模型为例,其转移矩阵的标准形式为:
则有:
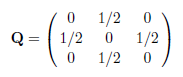
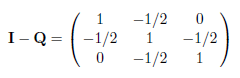
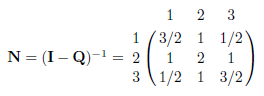
从N的中间一行可以看出,如果从状态2开始,则被吸收前到达状态1、2和3的平均转移次数分别为1、2和1。
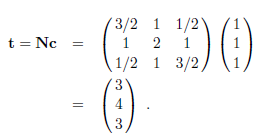
从状态1、2和3出发,到达吸收状态的平均转移次数分别为3、4和3。
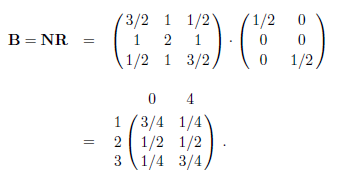
由矩阵B的第一行可知,从状态1出发,有3/4的概率到达吸收状态0,有1/4的概率到达吸收状态4。
参考:
[1] Chapter 11, Introduction to Probability, http://goo.gl/gjfsd
[1] Chapter 11, Introduction to Probability, http://goo.gl/gjfsd