## n位二进制表示的最大值 雪花算法已经初步完成了。现在我们再来看几个位操作。先看第一个,还是左移操作,不过这里演示负数左移: ``` << ``` 看这个之前,我们先看一个关键的数字,最大的负整数,-1L转换为二进制后的形式:
这里注意二进制数字的思路是相反的,在负整数中,除去负号外,那个数字越大,这个负数就越小,在Java的二进制形式中,首位代表正负号,除去首位,剩下的数字值越大,真的就代表数字本身越大,无论正负。从上面打印可以看出,-1L的二进制形式就是一个最大负整数。
我们前面讨论位运算提到过左移运算 << ,那么负数左移会出现什么情况的呢?下面来看一个例子:
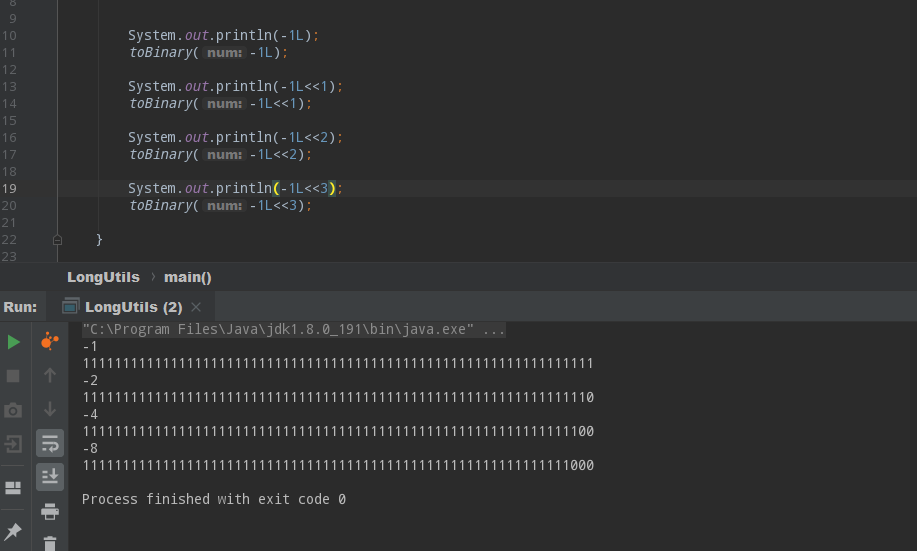
从字面值上来看,负整数左移和正整数左移效果是一样的,就是把字面值变小了,二进制的形式也能看出,所有的1左移后,右面直接补0,效果也是把数字变小了。
前面我们说过两个位移操作,那两个我们主要是关注二进制形式的数字效果,这里我们就要看字面值的变化了。-1L向左位移1位,字面值就变成
-1L * 2^1
如果向左位移n位,字面值就会变成:
-1L * 2^n
这就是-1L向左位移的字面值变化规律。
看完负数左移操作,再来看一个位移操作,取反操作:
~
取反的意思也是针对二进制形式的数字说的,因为所有位上的数字不是0就是1,所以取反的操作就是把0变成1,把1变成0,来看几个例子:
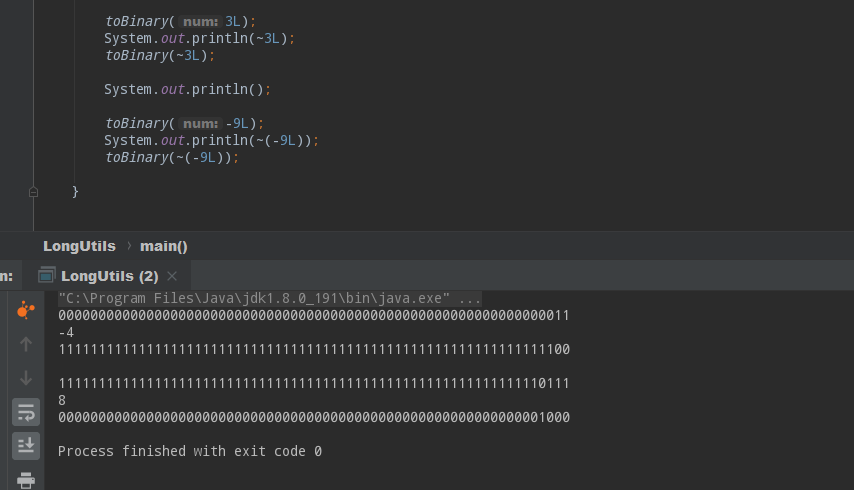
上面的正整数3L,取反后,字面值变成了-4L,二进制的数字中的0和1也彻底反了,0变成1,1变成0。而负整数-9L字面值变成了8L,二进制数字的变化也是一样的规律。大家可以多试几次,从上面的内容可以总结出取反的规律:
1、取反后,正整数变成了负整数,负整数变成了正整数
2、取反后,无论原来是正数还是负数,结果都会变成 (n+1) * -1L
取反操作我们也不看二进制数字的变化,但看字面值的变化,可以总结出上面的规律。
现在有个需求,如果有三位二进制数,那么能表示的最大正数就是 111,也就是7,如果有四位就是1111,也就是15,如果有n位如何用位运算表示?其实公式很容易推出来,就是
2^n-1
这个公式和上面的负数左移很相似,我们来使用-1L进行左移:
-1L << n
这样n如果是3和4就分别对应-8L和-16L,从字面值上看和我们的需求很接近,我们再来进行取反操作:
~(-1L << n)
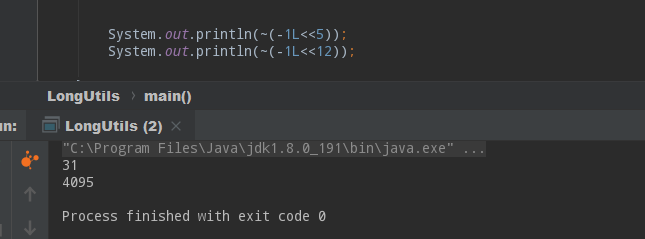
这样3和4分别对应的就是7和15了!上面这个位运算公式,就是求出n位二进制数能表示的最大整数的公式!
再来看雪花算法中的限制,数据中心id和机器id分别占5位,最大数都是31,毫秒内序列占12位,最大值是4095,这个值直接定义上是最快的,现在也可以用高效的位运算计算出来了:
不超过最大值的序列递增
雪花算法的毫秒内序列有两个操作,一个是在同一毫秒内加一,另一个是如果超过最大值,就强制等到下一个不同的时间从新开始序列。这里也是可以用位操作实现的。这里首先讨论下面的位操作:
&
这个操作的意思是同一个位上,都是1,结果才是1,否则就是0.下面用二进制数字演示一下:
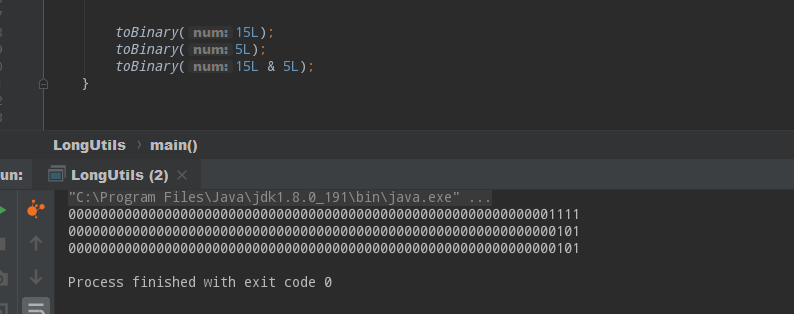
15L 转换为2进制形式后有个特点,就是前面所有位上都是1,那么这个时候,其实较小的数是多少结果就是多少。从而可以推理出,只要较大的数有这个特点,那么&操作的结果都和较小的数的值一样。如果超过最大值会怎么样呢?
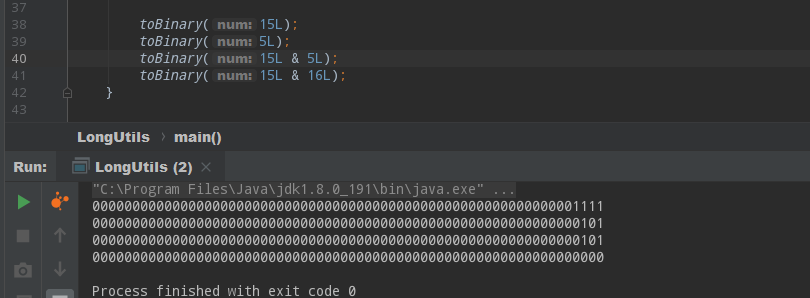
可以看到,只要超过1,那么结果就会归0,再加上1, 15L & 17L的话,结果又会是1。这样的&操作可以防止数字超过某个最大限制。这种特性正好用在毫秒内序列的加一操作上。
seq = (seq + 1) & 4095;
像上面那种写法,其实最终值和
seq = seq + 1
效果是一样的,不同的是,一旦超过了4095,seq会从新变成0。
代码地址:https://gitee.com/blueses/snowflake-demo 06