洛谷P2486 [SDOI2011]染色

原题传送门

题目描述

输入输出格式

输入格式：

输出格式：

对于每个询问操作，输出一行答案。

输入输出样例

输入样例#1： 

6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

输出样例#1： 

3
1
2

说明

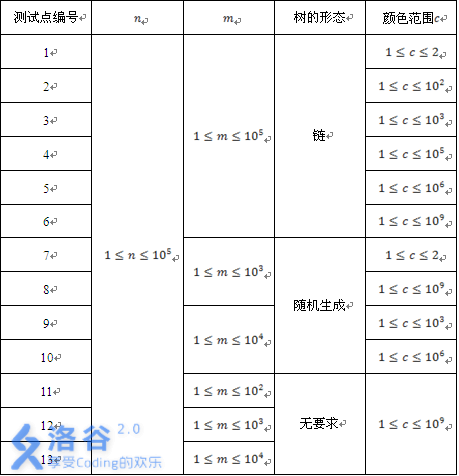
题解

看到一棵树，看到区间操作，首先想到的就是树链剖分+线段树。

这道题是非常规区间操作的典型题（需要合并区间）

这道题的线段树部分不是求和或区间最值，而是某种特定的区间操作（区间赋值+区间查询连续相同值段数），故需要更改push_up的部分

inline void push_up(int x){
    L[x]=L[x<<1];
    R[x]=R[x<<1|1];
    cnt[x]=cnt[x<<1]+cnt[x<<1|1]-(R[x<<1]==L[x<<1|1]);
}

我们记录每一段区间左右端点的颜色，合并时如果左区间的右端点的颜色和右区间的左端点的颜色相同，需要将计数器减1

至于线段树的其他部分，也要相应地做一些简单改变，具体见代码

树链剖分的路径查询环节也要改一下，需要支持区间合并，即当两段链交界处颜色相同时需要将计数器减1

int ret=0,l=-1,r=-1;
while(top[ii]!=top[jj]){
    if(de[top[ii]]<de[top[jj]]){
        swap(ii,jj);
        swap(l,r);
    }
    ret+=query(1,1,N,dfn[top[ii]],dfn[ii]);
    if(l==Rc){
        ret--;
    }
    l=Lc;
    ii=f[top[ii]];
}
if(de[ii]<de[jj]){
    swap(ii,jj);
    swap(l,r);
}
ret+=query(1,1,N,dfn[jj],dfn[ii]);
if(l==Rc){
    ret--;
}
if(r==Lc){
    ret--;
}
printf("%d
",ret);

注意这段代码中的Lc和Rc是模板中没有的。Lc是全局变量，表示当前查询区间的左端点的颜色，Rc也是全局变量，表示当前查询区间右端点的颜色

Lc和Rc可以在query函数中顺便求得

int query(int x,int l,int r,int ql,int qr){
    if(l>r||l>qr||r<ql){
        return 0;
    }
    if(l==ql){
        Lc=L[x];
    }
    if(r==qr){
        Rc=R[x];
    }
    if(ql<=l&&r<=qr){
        return cnt[x];
    }
    int mid=(l+r)>>1,ret=0;
    push_down(x,l,r);
    ret=query(x<<1,l,mid,ql,qr)+query(x<<1|1,mid+1,r,ql,qr);
    if(mid>=ql&&mid+1<=qr&&R[x<<1]==L[x<<1|1]){
        ret--;
    }
    return ret;
}

至此，所有的技术难题都解决了，题目也就迎刃而解了

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+7,MAXN=1e5+1,MAXM=2e5+1;
int N,M;
int head[MAXN],to[MAXM],nxt[MAXM],tp=1;
inline void add(int x,int y){
    nxt[++tp]=head[x];
    head[x]=tp;
    to[tp]=y;
    nxt[++tp]=head[y];
    head[y]=tp;
    to[tp]=x;
}
int f[MAXN],de[MAXN],son[MAXN],siz[MAXN];
void dfs1(int x,int fa,int d){
    f[x]=fa;
    de[x]=d;
    siz[x]=1;
    for(int i=head[x];i;i=nxt[i]){
        if(to[i]!=fa){
            dfs1(to[i],x,d+1);
            if(siz[to[i]]>siz[son[x]]){
                son[x]=to[i];
            }
            siz[x]+=siz[to[i]];
        }
    }
}
int dfn[MAXN],top[MAXN],timeclock;
int tmp[MAXN],val[MAXN],cnt[MAXN*3],tag[MAXN*3],L[MAXN*3],R[MAXN*3];
void dfs2(int x,int t){
    top[x]=t;
    dfn[x]=++timeclock;
    val[dfn[x]]=tmp[x];
    if(son[x]){
        dfs2(son[x],t);
    }
    for(int i=head[x];i;i=nxt[i]){
        if(to[i]!=f[x]&&to[i]!=son[x]){
            dfs2(to[i],to[i]);
        }
    }
}
inline void push_up(int x){
    L[x]=L[x<<1];
    R[x]=R[x<<1|1];
    cnt[x]=cnt[x<<1]+cnt[x<<1|1]-(R[x<<1]==L[x<<1|1]);
}
inline void push_down(int x,int l,int r){
    int &ii=tag[x];
    if(ii&&l!=r){
        tag[x<<1]=tag[x<<1|1]=ii;
        cnt[x<<1]=cnt[x<<1|1]=1;
        L[x<<1]=R[x<<1]=L[x<<1|1]=R[x<<1|1]=ii;
        ii=0;
    }
}
void init(int x,int l,int r){
    if(l==r){
        L[x]=R[x]=val[l];
        cnt[x]=1;
    }else{
        int mid=(l+r)>>1;
        init(x<<1,l,mid);
        init(x<<1|1,mid+1,r);
        push_up(x);
    }
}
void update(int x,int l,int r,int ql,int qr,int c){
    if(l>r||l>qr||r<ql){
        return;
    }
    if(ql<=l&&r<=qr){
        L[x]=R[x]=tag[x]=c;
        cnt[x]=1;
        return;
    }
    push_down(x,l,r);
    int mid=(l+r)>>1;
    update(x<<1,l,mid,ql,qr,c);
    update(x<<1|1,mid+1,r,ql,qr,c);
    push_up(x);
}
int Rc,Lc;
int query(int x,int l,int r,int ql,int qr){
    if(l>r||l>qr||r<ql){
        return 0;
    }
    if(l==ql){
        Lc=L[x];
    }
    if(r==qr){
        Rc=R[x];
    }
    if(ql<=l&&r<=qr){
        return cnt[x];
    }
    int mid=(l+r)>>1,ret=0;
    push_down(x,l,r);
    ret=query(x<<1,l,mid,ql,qr)+query(x<<1|1,mid+1,r,ql,qr);
    if(mid>=ql&&mid+1<=qr&&R[x<<1]==L[x<<1|1]){
        ret--;
    }
    return ret;
}
int main(){
    scanf("%d%d",&N,&M);
    for(int i=1;i<=N;i++){
        scanf("%d",tmp+i);
    }
    for(int i=1;i<N;i++){
        int ii,jj;
        scanf("%d%d",&ii,&jj);
        add(ii,jj);
    }
    dfs1(1,1,1);
    dfs2(1,1);
    init(1,1,N);
    for(int i=1;i<=M;i++){
        char op;
        int ii,jj,kk;
        scanf(" %c",&op);
        if(op=='C'){
            scanf("%d%d%d",&ii,&jj,&kk);
            while(top[ii]!=top[jj]){
                if(de[top[ii]]<de[top[jj]]){
                    swap(ii,jj);
                }
                update(1,1,N,dfn[top[ii]],dfn[ii],kk);
                ii=f[top[ii]];
            }
            if(de[ii]<de[jj]){
                swap(ii,jj);
            }
            update(1,1,N,dfn[jj],dfn[ii],kk);
        }else{
            scanf("%d%d",&ii,&jj);
            int ret=0,l=-1,r=-1;
            while(top[ii]!=top[jj]){
                if(de[top[ii]]<de[top[jj]]){
                    swap(ii,jj);
                    swap(l,r);
                }
                ret+=query(1,1,N,dfn[top[ii]],dfn[ii]);
                if(l==Rc){
                    ret--;
                }
                l=Lc;
                ii=f[top[ii]];
            }
            if(de[ii]<de[jj]){
                swap(ii,jj);
                swap(l,r);
            }
            ret+=query(1,1,N,dfn[jj],dfn[ii]);
            if(l==Rc){
                ret--;
            }
            if(r==Lc){
                ret--;
            }
            printf("%d
",ret);
        }
    }
    return 0;
}