因式分解

Table of contents

1. 基本概念
   1. 定义
   2. 相关结论
2. 一般步骤
3. 原则
4. 基本方法
   1. 提公因式法
   2. 公式法
   3. 十字相乘法
   4. 双十字相乘法
   5. 解方程法
   6. 分组分解法
   7. 拆项补项法
   8. 配方法
   9. 因式定理法
   10. 换元法
   11. 主元法
   12. 特殊值法
   13. 待定系数法
   14. 总结
5. 简单应用

基本概念

定义

　　把一个多项式在一个范围化为几个整式的积的形式，这种式子变形叫做这个多项式的因式分解，也叫作把这个多项式分解因式。

　　因式分解是中学数学中最重要的恒等变形之一，它被广泛地应用于初等数学之中，在数学求根作图、解一元二次方程方面也有很广泛的应用，是解决许多数学问题的有力工具。

　　因式分解方法灵活，技巧性强。学习这些方法与技巧，不仅是掌握因式分解内容所需的，而且对于培养解题技能、发展思维能力都有着十分独特的作用。学习它，既可以复习整式的四则运算，又为学习分式打好基础；学好它，既可以培养学生的观察、思维发展性、运算能力，又可以提高综合分析和解决问题的能力。

 

相关结论：

• 基本结论：分解因式与整式乘法为相反。
• 高级结论：在高等数学上因式分解有一些重要结论，在初等数学层面上证明很困难，但是理解很容易。

1. 因式分解与解高次方程有密切的关系。对于一元一次方程和一元二次方程，初中已有相对固定和容易的方法。在数学上可以证明，对于一元三次方程和一元四次方程，也有固定的公式可以求解。只是因为公式过于复杂，在非专业领域没有介绍。对于分解因式，三次多项式和四次多项式也有固定的分解方法，只是比较复杂。对于五次以上的一般多项式，已经证明不能找到固定的因式分解法，五次以上的一元方程也没有固定解法。
2.  所有的三次和三次以上的一元多项式在实数范围内都可以因式分解，所有的二次或二次以上的一元多项式在复数范围内都可以因式分解。这看起来或许有点不可思议。比如x⁴+1,这是一个一元四次多项式，看起来似乎不能因式分解。但是它的次数高于3，所以一定可以因式分解。也可以用待定系数法将其分解，只是分解出来的式子并不整洁。(这是因为，由代数基本定理可知n次一元多项式总是有n个根，也就是说，n次一元多项式总是可以分解为n个一次因式的乘积。并且还有一条定理：实系数多项式的虚数根两两共轭的，将每对共轭的虚数根对应的一次因式相乘，可以得到二次的实系数因式，从而这条结论也就成立了。)
3. 因式分解虽然没有固定方法，但是求两个多项式的公因式却有固定方法。因式分解很多时候就是用来提公因式的。寻找公因式可以用辗转相除法来求得。标准的辗转相除技能对于中学生来说难度颇高，但是中学有时候要处理的多项式次数并不太高，所以反复利用多项式的除法也可以但比较笨，不过能有效地解决找公因式的问题。
4. 因式分解是很困难的，初中所接触的只是因式分解很简单的一部分。

一般步骤

1. 如果多项式的首项为负，应先提取负号；
2. 如果多项式的各项含有公因式，那么先提取这个公因式，再进一步分解因式；
3. 如果各项没有公因式，那么可尝试运用公式、十字相乘法来分解；
4. 如果用上述方法不能分解，再尝试用分组、拆项、补项法来分解。

原则

1. 分解因式是多项式的恒等变形，要求等式左边必须是多项式。
2. 分解因式的结果必须是以乘积的形式表示。
3. 每个因式必须是整式，且每个因式的次数都必须低于原来多项式的次数。
4. 结果最后只留下小括号，分解因式必须进行到每一个多项式因式都不能再分解为止；
5. 结果的多项式首项一般为正。 在一个公式内把其公因子抽出，即透过公式重组，然后再抽出公因子；
6. 括号内的首项系数一般为正；
7. 如有单项式和多项式相乘，应把单项式提到多项式前。如(b+c)a要写成a(b+c)；
8. 考试时在没有说明化到实数时，一般只化到有理数就够了，有说明实数的话，一般就要化到实数。

基本方法（要求掌握打“*”的方法）

1.提公因式法*

　　如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法。

具体方法：

　　在确定公因式前，应从系数和因式两个方面考虑。当各项系数都是整数时，公因式的系数应取各项系数的最大公约数字母取各项的相同的字母，而且各字母的指数取次数最低的。当各项的系数有分数时，公因式系数为各分数的最大公约数。如果多项式的第一项为负，要提出负号，使括号内的第一项的系数成为正数。提出负号时，多项式的各项都要变号。

基本步骤：

1. 找出公因式；
2. 提公因式并确定另一个因式；
   1. 找公因式可按照确定公因式的方法先确定系数再确定字母；
   2. 提公因式并确定另一个因式，注意要确定另一个因式，可用原多项式除以公因式，所得的商即是提公因 式后剩下的一个因式，也可用公因式分别除去原多项式的每一项，求的剩下的另一个因式；
   3. 提完公因式后，另一因式的项数与原多项式的项数相同。

2.公式法*

完全平方公式

$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

平方差公式

$a^2-b^2=(a+b)*(a-b)$

立方和公式

$a^3+b^3=(a+b)*(a^2-ab+b^2)$

$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)$

立方差公式

$a^3-b^3=(a-b)*(a^2+ab+b^2)$

完全立方公式

$a^3+3a^2b+3ab^2+b^3=(a+b)^3$

两根式

$ax^2+bx+c=a(x-frac{-b+sqrt{b^2-4ac}}{2a})(x-frac{-b-sqrt{b^2-4ac}}{2a})$

3.十字相乘法*

若$a+b=p$，$a*b=q$则$x^2+px+q=(x+a)(x+b)$

当$k=ab$，$n=cd$，且$ad+bc=m$时，有$kx^2+mx+n=(ax+c)(bx+d)$

例：$6x^2+13x+5$

解：

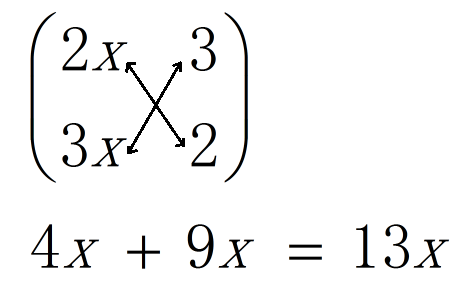
4.双十字相乘法

分解$ax^2+bxy+cy^2+dx+ey+f$

一般步骤：

1. 用十字相乘法分解二次项($ax^2+bxy+cy^2$)，得到一个十字相乘图(有两列)；
2. 把常数项f分解成两个因式填在第三列上，要求第二、第三列构成的十字交叉之积的和等于原式中的ey，第一、第三列构成的十字交叉之积的和等于原式中的dx．
3. 先以一个字母的一次系数分数常数项；
4. 再按另一个字母的一次系数进行检验；
5. 横向相加，纵向相乘。

例：$x^2+5xy+6y^2+8x+18y+12$

解：

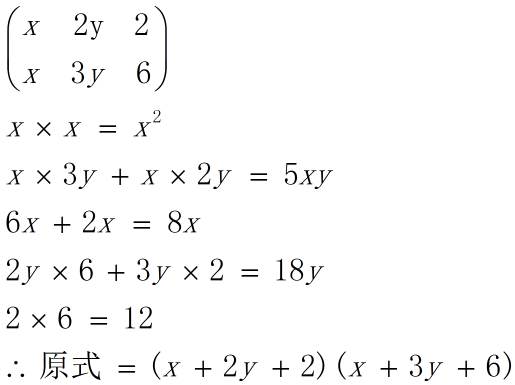
5.解方程法

通过解方程来进行因式分解

$ax^2+bx+c=a(x-frac{-b+sqrt{b^2-4ac}}{2a})(x-frac{-b-sqrt{b^2-4ac}}{2a})$

6.分组分解法*

　　通过分组分解的方式来分解提公因式法和公式分解法无法直接分解的因式，这种分解因式的方法叫做分组分解法。能分组分解的多项式有四项或大于四项，一般的分组分解有两种形式：二二分法，三一分法。

例1：因式分解ax+ay+bx+by

解：ax+ay+bx+by

　　=a(x+y)+b(x+y)

　　=(a+b)(x+y)

例4：因式分解ax+ay+bx+by

解：ax+ay+bx+by

　　=a(x+y)+b(x+y)

　　=(a+b)(x+y)

7.拆项补项法*

例:分解因式：x³-9x+8．

解法1： 将常数项8拆成-1+9．

原式=x³-9x-1+9

　　=(x³-1)-9x+9

　　=(x-1)(x²+x+1)-9(x-1)

　　=(x-1)(x²+x-8)

解法2：将一次项-9x拆成-x-8x．

原式=x³-x-8x+8

　　=(x³-x)+(-8x+8)

　　=x(x+1)(x-1)-8(x-1)

　　=(x-1)(x²+x-8)

解法3：将三次项x³拆成9x³-8x³．

原式=9x³-8x³-9x+8

　　=(9x³-9x)+(-8x³+8)

　　=9x(x+1)(x-1)-8(x-1)(x²+x+1)

　　=(x-1)(x²+x-8)

解法4：添加两项-x²+x²．

原式=x³-9x+8

　　=x³-x²+x²-9x+8

　　=x²(x-1)+(x-8)(x-1)

　　=(x-1)(x²+x-8)

8.配方法

　　对于某些不能利用公式法的多项式，可以将其配成一个完全平方式，然后再利用平方差公式，就能将其因式分解，这种分解因式的方法叫做配方法。属于拆项、补项法的一种特殊情况。也要注意必须在与原多项式相等的原则下进行变形。

 

例：分解因式x²+3x-40

解：x²+3x-40

　　=x²+3x+2.25-42.25

　　=(x+1.5)²-(6.5)²

　　=(x+8)(x-5)．

9.因式定理法

因式定理：

如果多项式$f(a)=0$，那么多项式$f(x)$必定含有因式$x-a$。反过来，如果$f(x)$含有因式$x-a$，那么，$f(a)=0$

根据因式定理，用求多项式的根来确定多项式的一次因式，从而对多项式进行因式分解的方法叫做因式定理法。

10.换元法*

　　选择多项式中的相同的部分换成另一个未知数，然后进行因式分解，最后再转换回来，这种分解因式的方法叫做换元法。注意，换元后勿忘还元。

 

例：分解因式(x²+x+1)(x²+x+2)-12

解：令y=x²+x,则

原式=(y+1)(y+2)-12

　　=y²+3y+2-12=y²+3y-10

　　=(y+5)(y-2)

　　=(x²+x+5)(x²+x-2)

　　=(x²+x+5)(x+2)(x-1)．

11.主元法

　　在分解含多个字母的代数式时，选取其中一个字母为主元(未知数),将其它字母看成是常数，把代数式整理成关于主元的降幂排列(或升幂排列)的多项式，再尝试用公式法、配方法、分组分解法等分解因式的方法进行分解。这种分解因式的方法叫做主元法。

 

例：因式分解(ab+bc+ca)(a+b+c)-abc.

解：

原式$=(b+c)a^2+(b^2+c^2+2bc)a+b(bc+c^2)$

　　$=(a+c)(b+c)(a+b)$

对于低次因式分解，主元法与十字相乘法的配合是卓有成效的。

12.特殊值法

将2或10代入x，求出数p，将数p分解质因数，将质因数适当的组合，并将组合后的每一个因数写成2或10的和与差的形式，将2或10还原成x，即得因式分解式。这种分解因式的方法叫做特殊值法。

13.待定系数法*

　　在因式分解时，一些多项式经过分析，可以断定它能分解成某几个因式，但这几个因式中的某些系数尚未确定，这时可以用一些字母来表示待定的系数。由于该多项式等于这几个因式的乘积，根据多项式恒等的性质，两边对应项系数应该相等，或取多项式中原有字母的几个特殊值，列出关于待定系数的方程(或方程组)，解出待定字母系数的值，这种因式分解的方法叫作待定系数法。

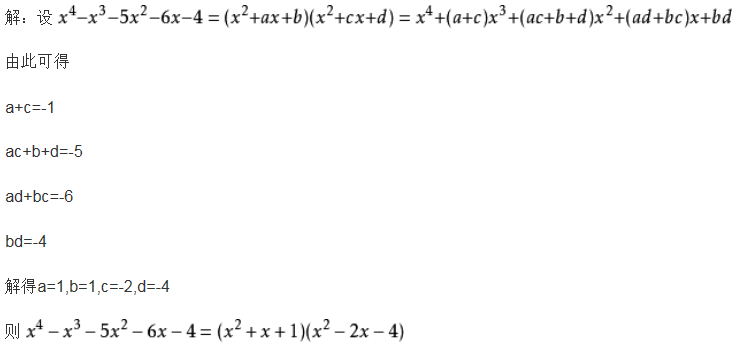
总结

上述的方法大致可以分为几类：

1. 多项式（宏观）处理：分组法、拆项法……
2. 具体（微观）操作：公式法、十字相乘法……
3. 特殊方法：方程法、特殊值法

应用