【codevs1576】最长严格上升子序列

0x01题面

给定一个长为n的序列，求它的最长上升子序列。 n<103$n<{10}^3$
子序列指序列中任意m个元素拼起来形成的新序列（可不连续）

0x02思路

1. 考虑任意一个长为m的上升子序列，他必然是由一个比他更短的(长为m-1)的上升子序列和一个比(那个长为m-1的子序列)末尾元素要大的值构成的。
2. 状态一：考虑第i个数能否与前面所有的上升子序列构成新的上升子序列。并找出其中最长的。
   即f[i]为到i为止的LIS的长度。转移就是他前面末尾小于他的元素能够成的最长的上升子序列长度+1。边界条件是：长为1的LIS必然长为1。
3. 状态二：
   思路：
   （a）考虑当前在上升子序列的末尾数是m，那他必然需要与一个比他更大的值构成新的更长的上升子序列。
   （c）那么f[i]保存的就是长度为i的LIS中末尾元素的最小值(这里是另一个贪心，因为所有相同长度的LIS末尾元素越小的，一定越容易在后面得到匹配)。
   误区：
   （b）即f[i]表示长度为i的LIS中末尾元素的最小值。（注意是所有任意长度为i的上升子序列，他们不一定是起始位置开始，可以从任何地方开始。）
   （d）f[i]不一定要大于f[i-1]，只有在同一层，用了相同个数的元素转移，划分在用一段内的时候，f[i]>f[i-1]才成立。
   转移：
   （e）如何得到长为i的LIS的末位最小值{1.找到后面第一个比他大的元素”1 9 7 8”。2.找到后面比他大的最小的元素(找不全)/找到所有数中比他大的元素(绕回去)：”1 7 8 9 2 4”。}都是不对的。
   （f）以”1 7 8 9 2 4”为例，找到所有数中比他大的元素转移顺序依次是1->2->4->7。
   ——是位置的锅。长为4的LIS的末位不可能是原序列中处于位置2的元素的值。——即第i个元素只能成为长度为1~i的LIS的末位，长度为i的LIS的末位一定属于原序列的[i,n]。
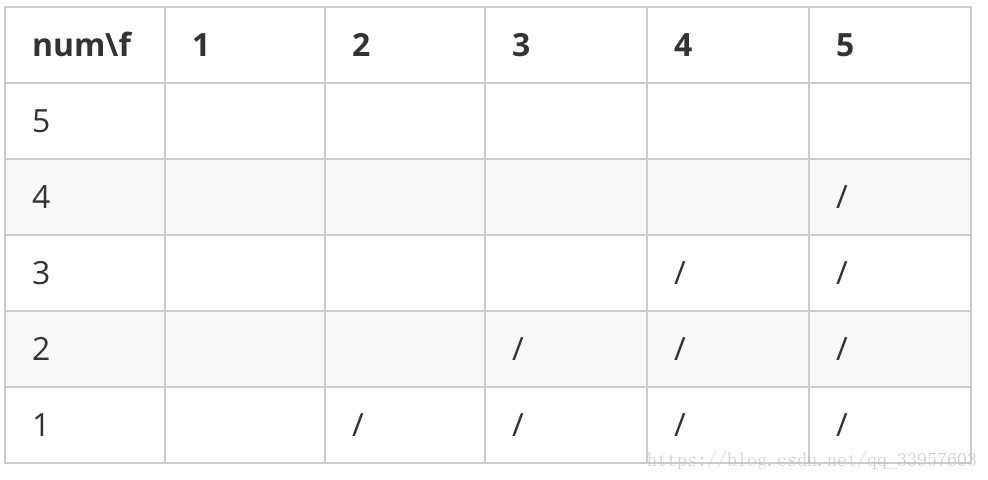
   （g）上一条写成全部状态就张这样，顺序是左下到右上。凑合着看吧。（线划掉的表示不存在的元素）（长为1的LIS末位有5种可能，长为2的有4种，长为3的有2种。。。）
   
   （h）这里状态转移要满足的条件为同一行(到第i个数为一段位置)，右边的要大于左边的值(长为i的LIS末位要大于长为i-1的LIS的末位)。
   （i）当且仅当存在长为i-1的LIS时，长为i的LIS的末位最小值才有意义。
   test：
   （z）循环顺序是枚举数组中所有的值，然后用每个这些值尝试去更新f[i]的值。

0x03代码

提交

//f[i]:到i为止的LIS的长度。
//f[i]=max{1,f[j]+1|j<i&&aj<ai}
#include<iostream>
#include<algorithm>
using namespace std;
int n, a[510], f[510], ans;
int main(){
    cin>>n;
    for(int i = 1; i <= n; i++)cin>>a[i];
    for(int i = 1; i <= n; i++){
        int t = 0;
        for(int j = 1; j < i; j++)
            if(a[j]<a[i])t = max(t, f[j]);
        f[i] = t+1;
        ans = max(ans, f[i]);
    }
    cout<<ans<<"
";
    return 0;
}

//f[i]:长度为i的LIS中末尾元素的最小值
//f[i] = max{f[i],aj|aj>f[i-1]}
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 1000010;
long long n, a[maxn], f[maxn], ans;//最后一个点有点大要开long long
int main(){
    cin>>n;
    for(int i = 1; i <= n; i++)cin>>a[i];
    memset(f,0x3f,sizeof(f));
    for(int j = 1; j <= n; j++)
        for(int i = 1; i <= j; i++)//扫描序列判断是否能更新
            if(i==1 || a[j]>f[i-1])//i=1要特判因为f[1]为序列中所有元素的最小值。
                f[i] = min(f[i], a[j]);
    for(int i = n; i >= 1; i--)
        if(f[i]<f[0])
            { cout<<i<<"
"; return 0; }
    return 0;
}