JAVA作业 02 JAVA语法基础

一、

思考问题一：枚举类型

public class EnumTest {

public static void main(String[] args)

{ Size s=Size.SMALL;

Size t=Size.LARGE; //s和t是否引用同一个对象

System.out.println(s==t); //是原始数据类型吗？

System.out.println(s.getClass().isPrimitive()); //从字符串中转换

Size u=Size.valueOf("SMALL");

System.out.println(s==u); 

for(Size value:Size.values())

{ System.out.println(value); }

}}  enum Size{SMALL,MEDIUM,LARGE};

1结果截图示例

 

2 实验分析

枚举类型的每个具体值都引用一个特定的对象，相同值引用同一个对象。因为s和t是不同内容所以引用不同对象。

枚举是引用型变量，枚举类型关键字是enum，类型名自己根据需要定义，可以通过定义变量名来遍历。valueOf() 类型转换,将后边的类型转换成前边的类型。可以在类中定义，也可以在类外定义。

可以使用“==”和equals()方法直接比对枚举变量的值，换句话说，对于枚举类型的变量，“==”和equals()方法执行的结果是等价的。

1）定义

enum 类型名 {内容1，内容2，.....内容n}；

2）引用

类型名 变量名=类型名.内容

3）遍历

for( 类型名 变量名:类型名.values()){

System.out.println(变量名); }

二、

思考问题二：反码 原码和补码

1 在计算机内，定点数有3种表示法：原码、反码和补码。原码、反码、补码是相对于整数来说，都是8位二进制表示一个数。反码是数值存储的一种，但是由于补码更能有效表现数字在计算机中的形式，所以多数计算机一般都不采用反码表示数。

1）原码 

 最高位为符号位；正数最高位为0，负数为1.

范围 -127~+127

例 +11的原码是00001011，-11原码是10001011.

2）反码

正数的反码与其原码相同；负数的反码是对其原码逐位取反，但是符号位不变。

范围

-127~+127

例 +11的反码是00001011，-11的反码是11110100

3）补码

正数的补码原码一样；负数的补码是在其反码的末位加一。

范围-128~+127

例 +11补码 00001011，-11补码10000101

2 示例程序

 （-83）+（-80）=？

1 0 1 0 1 1 0 1 B -83

1 0 1 1 0 0 0 0 B -80

0 1 0 1 1 1 0 1 B +93

思考：这两个题目，按照正常的法则来运算，但结果显然不正确，这是怎么回事呢？

答案：这是因为发生了溢出。

如果计算机的字长为n位，n位二进制数的最高位为符号位，其余n-1位为数值位，采用补码表示法时，可表示的数X的范围是 -2的n-1次幂≤X≤2的n-1次幂-1

当n=8时，可表示的有符号数的范围为-128～+127。两个有符号数进行加法运算时，如果运算结果超出可表示的有符号数的范围时，就会发生溢出，使计算结果出错。很显然，溢出只能出现在两个同符号数相加或两个异符号数相减的情况下。

对于加法运算，如果次高位（数值部分最高位）形成进位加入最高位，而最高位（符号位）相加（包括次高位的进位）却没有进位输出时，或者反过来，次高位没有进位加入最高位，但最高位却有进位输出时，都将发生溢出。因为这两种情况是：两个正数相加，结果超出了范围，形式上变成了负数；两负数相加，结果超出了范围，形式上变成了正数。

而对于减法运算，当次高位不需从最高位借位，但最高位却需借位（正数减负数，差超出范围），或者反过来，次高位需从最高位借位，但最高位不需借位（负数减正数，差超出范围），也会出现溢出。

在计算机中，数据是以补码的形式存储的，所以补码在c语言的教学中有比较重要的地位，而讲解补码必须涉及到原码、反码。

在n位的机器数中，最高位为符号位，该位为零表示为正，为一表示为负；其余n-1位为数值位，各位的值可为零或一。当真值为正时，原码、反码、补码数值位完全相同；当真值为负时，原码的数值位保持原样，反码的数值位是原码数值位的各位取反，补码则是反码的最低位加一。注意符号位不变。

 

 三、

思考问题三：同名变量的屏蔽原则

1.原则：局部变量的名字和全局变量的名字相同，在局部变量的有效范围内，全局变量将失去作用。

 2.示例

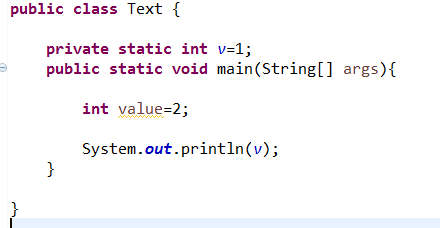
输出 1，没有屏蔽，因为不同名。

 输出2，因为同名，但是在主函数的作用域内，所以以2为主。

四、

思考问题四：浮点数在计算机内部的表示方法

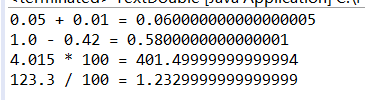
1. 为什么用double类型计算得不到数学上的精确结果？

无论是单精度还是双精度在存储中都分为三个部分：

1. 符号位(Sign) : 0代表正，1代表为负
2. 指数位（Exponent）:用于存储科学计数法中的指数数据，并且采用移位存储
3. 尾数部分（Mantissa）：尾数部分

这个涉及到二进制与十进制的转换问题。计算机是二进制的。浮点数没有办法是用二进制进行精确表示。我们的CPU表示浮点数由两个部分组成：指数和尾数，这样的表示方法一般都会失去一定的精确度，有些浮点数运算也会产生一定的误差。

N进制可以理解为：数值×基数的幂，例如我们熟悉的十进制数123.4=1×10²+2×10+3×(10的0次幂)+4×(10的-1次幂)；其它进制的也是同理，例如二进制数11.01=1×2+1×(2的0次幂)+0+1×(2的-2次幂)=十进制的3.25。 double类型的数值占用64bit，即64个二进制数，除去最高位表示正负符号的位，在最低位上一定会与实际数据存在误差（除非实际数据恰好是2的n次方）。
举个例子来说，比如要用4bit来表示小数3.26，从高到低位依次对应2的1,0,-1,-2次幂，根据最上面的分析，应当在二进制数11.01(对应十进制的3.25)和11.10(对应十进制的3.5)之间选择。 简单来说就是我们给出的数值，在大多数情况下需要比64bit更多的位数才能准确表示出来（甚至是需要无穷多位），而double类型的数值只有64bit，后面舍去的位数一定会带来误差，无法得到“数学上精确”的结果。

2.在构建BigDecimal对象时应使用字符串而不是double数值，否则，仍有可能引发计算精度问题。（为什么会这样呢？）

 由于浮点数采用二进制系统表示，而二进制无法精确的表示1/10，好比十进制无法精确表示1/3一样。因此，对于很多值浮点数都是采用其能够表示的离目标值近的数来表示，这有可能会在计算中带来不易察觉的误差。为了解决基本数据类型浮点数不能进行精确计算的问题，java中专门提供了java.math.BigDecimal类，其提供浮点数的精确计算功能。

五、

思考问题五：

以下代码的输出结果是什么？为什么会有这样的输出结果？

int X=100;
int Y=200;

System.out.println("X+Y="+X+Y);
System.out.println(X+Y+"=X+Y");

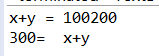
因为第一个输出 “x+y=” 是以字符形式输出的，字符和任何数据类型相加都是相连接，形成一个更大的字符串；第二个x和y先做加法运算，再输出300=x+y。

六、

课后实验性问题：编写一个程序，用户输入两个数，求出其加减乘除，并用消息框显示计算结果。

1.程序设计思想：首先在框架中输入两个字符串，转化为整形，然后输入一个符号，利用条件语句判断它是什么运算符号，计算、输出结果（符号输入不符合四则运算的提示错误）。

2.程序流程图：

            

3.源程序：

//2016/9/30

import javax.swing.JOptionPane;

public class Addition {

public static void main(String[] args) {

String firstNumber,secondNumber,sym;

int number1,number2;

float num;

firstNumber = JOptionPane.showInputDialog("Enter first integer");

secondNumber = JOptionPane.showInputDialog("Enter second integer");

sym = JOptionPane.showInputDialog("Input the symbol");

number1 = Integer.parseInt(firstNumber);

number2 = Integer.parseInt(secondNumber);

if(sym.equals("+"))

{

num = number1 + number2;

JOptionPane.showMessageDialog(null,number1 + "+" + number2 + "=" + num);

}

else if(sym.equals("-"))

{

num = number1 - number2;

JOptionPane.showMessageDialog(null,number1 + "-" + number2 + "=" + num);

}

else if(sym.equals("*"))

{

num = number1 * number2;

JOptionPane.showMessageDialog(null,number1 + "*" + number2 + "=" + num);

}

else if(sym.equals("/"))

{

num = number1 / number2;

JOptionPane.showMessageDialog(null,number1 + "/" + number2 + "=" + num);

}

else

{

JOptionPane.showMessageDialog(null,"Error!");

}

}

}

4.验证结果截图：

 

5.实验总结：1）在判断字符中“==”和equals分不太清楚；2）在判断字符是否相等时，开始用的单引号，后来才反应过来输入符号时用的是字符串类型，应该改为双引号。

查看全文