题型:
分析题30
简答题40
应用题30 (写程序10分) .
今年比较特殊,好像题比往年简单,然而我还是感到头秃。
第1章
计算时间复杂度

注意:
一个语句本身的程序步数可能不等于该语句一次 执行所具有的程序步数。
例如:赋值语句 x = sum (R, n) 赋值操作的程序步数为 1;
一次执行对函数 sum (R, n) 的调用需要的程序步 数为 2 * n+3;
一次执行的程序步数为 1+2 * n+3 = 2 * n+4
大O的表示方法
T(n) = O(f(n)) 称f(n)为算法的“渐进”时间复杂度 ,简称时间复杂度,以简化算法复杂性的分析。
说明:在计算算法时间复杂度时,可以忽略所有低次幂和最高次幂的系数。
大O的运算规则
• 加法准则(并列程序段 )
前提:(T_1)(m) = O(f(m)); (T_2)(n) = O(g(n))
结论:(T)(n)= (T_1)+(T_2) = O(f(n)+g(n))
(T)(n) = (T_1)+(T_2) = O(max(f(m),g(n)))
• 乘法准则(嵌套程序段)
前提:(T_1)(n) = O(f(n)); (T_2)(n) = O(g(n))
结论:(T)(n) = (T_1)* (T_2) = O(f(n)*g(n))
常见函数的增长率

例1
void exam ( float x[ ][ ], int m, int n ) {
float sum [ ];
for ( int i = 0; i < m; i++ ) { //x中各行
sum[i] = 0.0; //数据累加
for ( int j = 0; j < n; j++ )
sum[i] += x[i][j];
}
for ( i = 0; i < m; i++ ) //打印各行数据和
cout << i << “ : ” <<sum [i] << endl;
}
//渐进时间复杂度为 O(max (m*n, m))
例2
void bubble_sort(int a[], int n ) {
//用冒泡排序方法,将a 中n个整数的序列排列成自小至大有序的整数序列。
int change ,i;
for (i = n-1,change=1; i >=1&&change; - -i ){
change= 0;
for (j = 0; j<i; ++j )
if (a [j] >a[ j+1]) {
a [j]<->a[ j+ 1]
change=1;}
}
}// bubble_sort
//基本操作:赋值操作。时间复杂度:O(n^2)--最坏情况下时间复杂度
BubbleSort n-1趟 BubbleExchange ( ) n-i次比较
当输入的数据已经排好序, 只要比较n-1次, 当输入的数据是减序,需要 比较n(n-1)/2次。
第2、3章
线性结构:
栈和队列
栈序列
栈队列的边界条件
双向循环链的基本操作
循环队列的判空判满操作
第4章
一维数组求地址
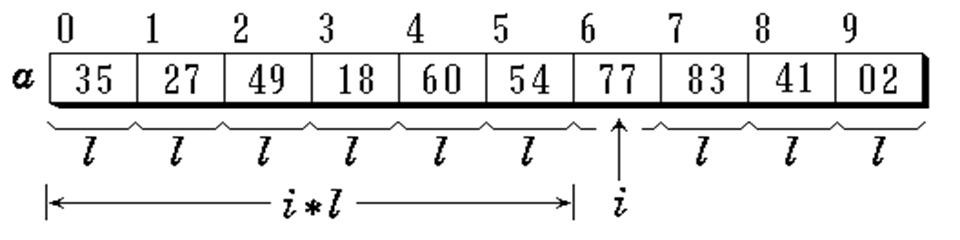
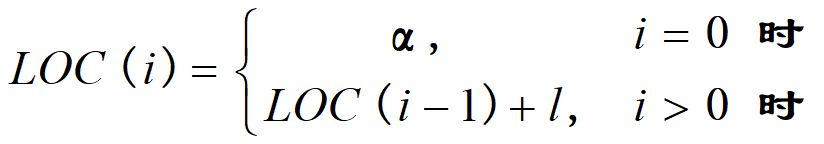
递推式 (LOC ( i ) = LOC ( i -1 ) + l =α+ i*l)
二维数组求地址
n行m列的二维数组:
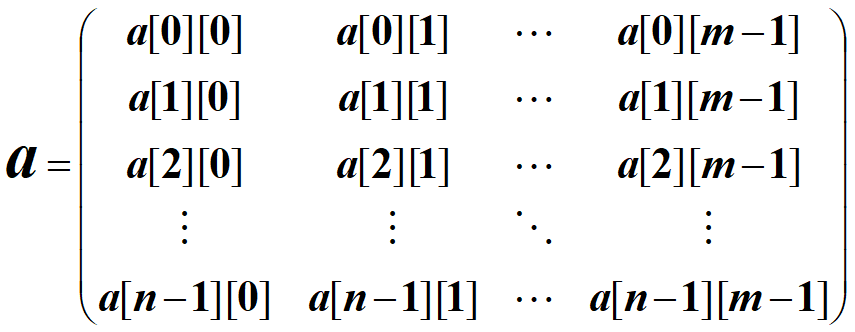
行优先 (LOC ( j, k ) = a + ( j * m + k ) * l)
n维数组
各维元素个数为 (m_1), (m_2), (m_3), …, (m_n)
下标为 (i_1), (i_2), (i_3), …, (i_n) 的数组元素的存储地址:
(LOC) ( (i_1), (i_2), …, (i_n) ) = a +
( (i_1)* (m_2)* (m_3)* …* (m_n) + (i_2)* (m_3)* (m_4)* …* (m_n)+……+ (i_{n-1})*(m_n) + (i_n) ) * l
=a+( (sum_{j=1}^{n-1})(i_j) *(prod_{k=j+1}^{n})(m_k)+(i_n)) *l
★第5章
树(要求代码):
树的特性(知道其推导过程)
树的遍历(深度和层次遍历及其应用)
树的建立(先根和后根序列确定一棵树)
树和二叉树的转换,
堆
哈夫曼树及编码
第6章
集合:
散列表:创建和冲突检测、查找长度( 成功和非成功)
第7章
搜索:
折半搜索原理及适用条件
二叉判定树的结构
三叉排序树的创建和删除
第8章
图(掌握原理):
图的存储结构
深度和广度序列
图(强)连通,(强)连通分量
最小生成树算法
最短路径和最短路径长度
拓扑排序
第9章
排序算法(掌握原理)
直接插入、折半插入、希尔排序、冒泡、快排(重点)、简单选择、堆排序